







岡山県の2021年3月実施の令和3年度(2021年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の岡山県の数学は6つの大問で構成され、小問集合、方程式、関数、、資料の活用、図形となっています。
難易度はやや易です。数学が得意なお子さんは満点が狙えると思います。
特に小問集合と方程式の分野が簡単です。また、関数や資料の活用は最終問題までは解けるようにしておきましょう。
図形問題は一番難易度が高いです。ただ、しっかりと見ていけば同じく最終問題までは解けると思います。
①-3-(-7)
【答え】4
【解説】負の数と負の数を掛けると正の数になります。
-3-(-7)=-3+7=4
②(-5)×4
【答え】-20
【解説】負の数と正の数を掛けると負の数になります。
(-5)×4=-(5×4)=-20
③3(a-2b)-2(a+b)
【答え】a-8b
【解説】同類項をまとめましょう。
3(a-2b)-2(a+b)=3a-6b-2a-2b=a-8b
④10ab²÷(-2b)
【答え】-5ab
【解説】割り算は文字の次数が下がることに注意しましょう。
10ab²/(-2b)=-5ab
⑤(√7+√5)(√7-√5)
【答え】2
【解説】公式(a+b)(a-b)=a²-b²を用いると楽です。
(√7)²-(√5)²=2
⑥方程式x²-5x+1=0を解きなさい。
【答え】x=(5±√21)/2
【解説】解の公式「ax²+bx+c=0の時x=-b±√b²-4ac/2a」にa=1,b=-5,c=1を代入すると
x=-(-5)±√(-5)²-4×1×1/2×1
x=(5±√21)/2
⑦次の図の(1)~(3)は、関数y=-2x²、y=x²、及びy=1/2x²のグラフを、同じ座標軸を使って描いたものです。図の(1)~(3)を表した関数の組み合わせとして最も適当なものは、ア~カのうちのどれですか。一つ答えなさい。ただし、点Oは原点とします。
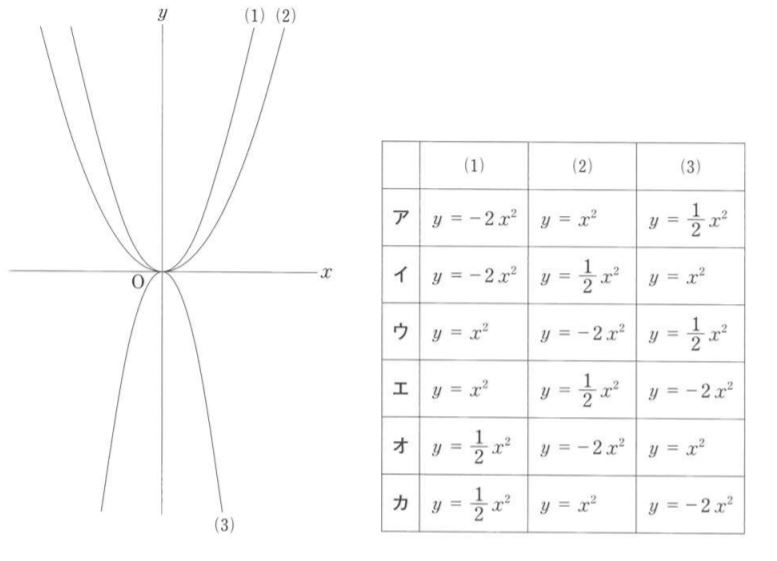
【答え】エ
【解説】(3)が上に凸より係数は負数、よってエまたはカ。(1),(2)を比較した時に変化の割合が大きい方がグラフの開きは小さくなるので、(1)の方が(2)よりもy=ax²のaの値が大きいはずなので、答えはエとなる。
⑧大小2つのさいころを同時に投げるとき、出る目の数の和が5以下となる確率を求めなさい。ただし、サイコロの1から6までの目の出方は、同様に確からしいものとします。
【答え】5/18
【解説】大小2つのさいころを同時に投げるとき、全通りは6×6=36通り
出る目の数の和が5以下となるようなケースは次の10通り
5→(1,4)(2,3)(3,2)(4,1)
4→(1,3)(2,2)(3,1)
3→(1,2)(2,1)
2→(1,1)
よって、10/36=5/18
⑨次の図のような、底面が点Oを中心とする円で、点Aを頂点とする円錐があります。底面の円の円周上に点Bがあり、AB=7cm、OB=3cmのとき、この円錐の体積を求めなさい。ただし、答えを求めるまでの過程も書きなさい。
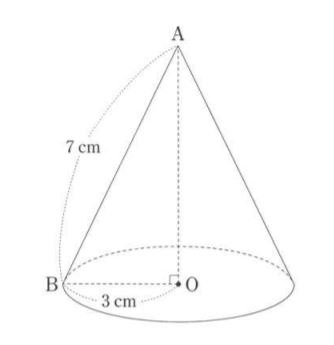
【答え・解説】
△ABOにおいて∠AOB=90°なので
三平方の定理より
AO²+3²=7²
AO²=40
AO>0なので、AO=2√10
よって、求める体積は
1/3×π×3²×2√10=6√10π
⑩次の図のような△ABCについて、【条件】を満たす点Dを、定規とコンパスを使って作図しなさい。作図に使った線は残しておきなさい。
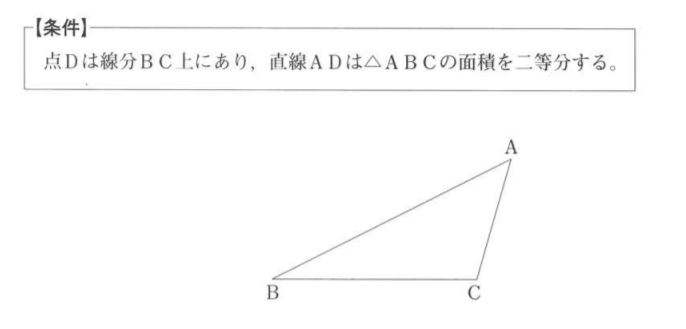
【答え】下図参照
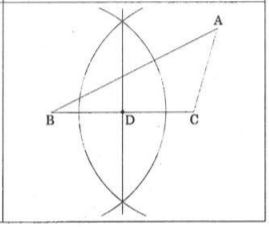
【解説】【条件】から点Dは線分BCの垂直二等分線と線分BCの交点であることがわかるので、点B,Cからコンパスである半径で弧を描き、それぞれの交点を通るような直線を引く。線分BCとの交点が点Dである。
数学の授業で、太郎さんと花子さんは次の【問題】について考えています。①~③に答えなさい。
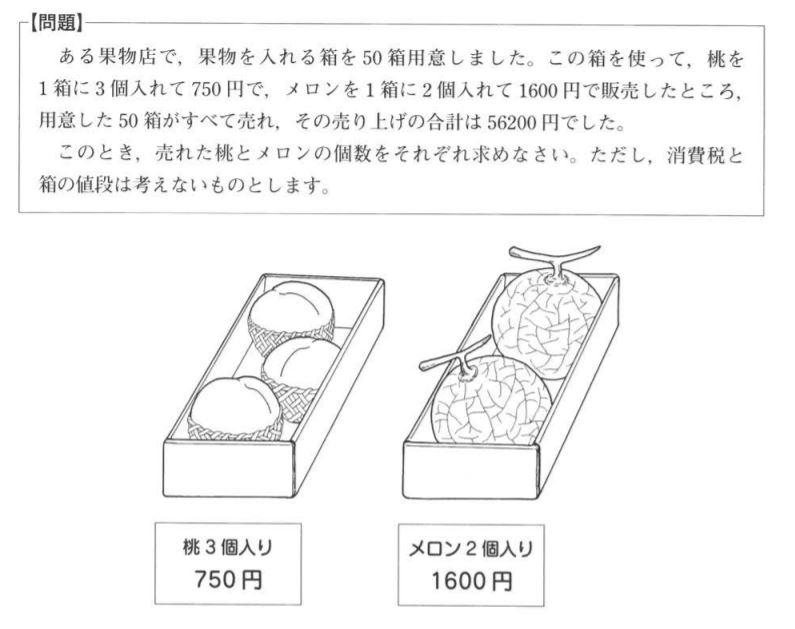
①太郎さんは【問題】について、次のように解き方を考えました。<太郎さんの考え>の(1)(2)に適当な式を書きなさい。

(1)
【答え】50-a
【解説】桃を入れた箱とメロンを入れた箱の合計は50であるから、桃を入れた箱の数をaとすればメロンの箱の数は50-aとなる。
(2)
【答え】750a+1600(50-a)
【解説】桃の箱の数がa,メロンの箱の数が50-aであるから、箱の個数に値段をかけたものの和が売り上げの合計となる。
②花子さんは【問題】について、太郎さんとは別の解き方を考えました。<花子さんの考え>の(3)(4)に適当な式を書きなさい。

(3)
【答え】250x+800y
【解説】桃の個数に値段をかけたもの、メロンの個数に値段をかけたものの合計が売り上げの合計である。
(4)
【答え】x/3+y/2
【解説】桃は一箱に3個、メロンは一箱に2個入っていることから(桃の個数)/3と(メロンの個数)/2の合計が50箱になる
③売れた桃とメロンの個数をそれぞれ求めなさい。
【答え】桃:84(個)メロン:44(個)
【解説】750a+1600(50-a)=56200をとくとa=28,桃の箱数が28,メロンの箱数が22とわかるのでそれぞれの個数が求められる
次の図は、反比例の関係y=a/xのグラフです。ただし、aは正の定数とし、点Oは原点とします。①~③に答えなさい。
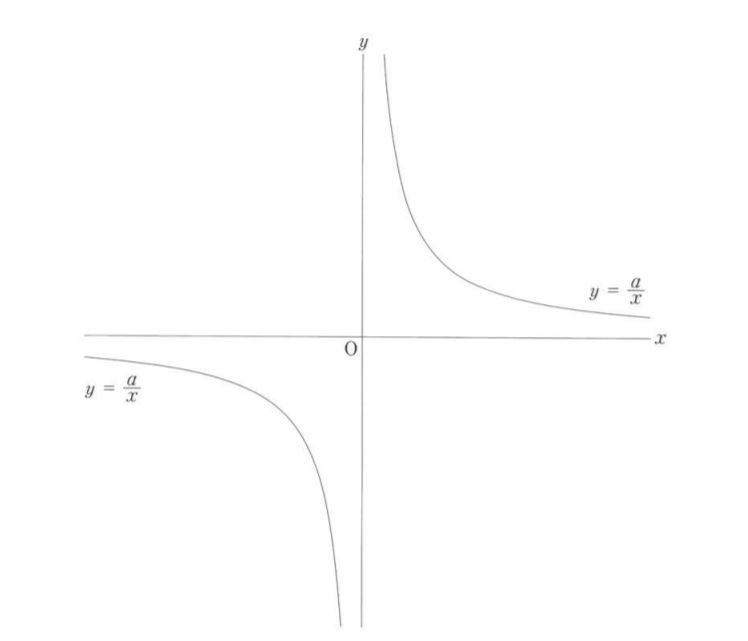
①yがxに反比例するものは、ア~エのうちでどれですか。当てはまるものを全て答えなさい。
ア:面積が20cm²の平行四辺形の底辺xcmと高さycm
イ:1辺がxcmの正六角形の周の長さycm
ウ:1000mの道のりを毎分xmの速さで進む時にかかる時間y分
エ:半径xcm、中心角120°のおうぎ形の面積ycm²
【答え】ア、ウ
【解説】y=a/xの形を満たすものを選ぶ。
ア:平行四辺形の面積は底辺×高さ÷2となるので、y=40/x
イ:y=6x
ウ:y=1000/x
エ:おうぎ形の面積は半径×半径×中心角/360なので、y=1/3x²
②グラフが点(4,3)を通るとき、(1)(2)に答えなさい。
(1)aの値を求めなさい。
【答え】a=12
【解説】y=a/xの式に代入、aについて解く。
3=a/4
a=12
(2)xの変域が3≦x≦8のとき、yの変域を求めなさい。
【答え】3/2≦y≦4
【解説】それぞれのxの値を(1)で求めたy=12/xに代入すると
x=3のとき、y=4
x=8のとき、y=3/2
③aは6以下の正の整数とします。グラフ上の点のうち、x座標とy座標がともに整数である点が4個となるようなaの値を、すべて求めなさい。
【答え】a=2,3,5
【解説】1≦a≦6(a:整数)でy=a/xのグラフは第一象限(右上)、第三象限(左下)に存在するので、
グラフ上に4つの整数の点が存在する場合、y=a/xは対称なグラフなので、各象限に2つずつ整数の点が存在すればよい。
各象限におけるグラフに2つずつ整数の点が存在するときはx=a,x=1の時のみであるから、aは6以下の素数であることがわかる。
よってa=2,3,5
太郎さんと花子さんは、今年のスギ花粉の飛散量を予想しているニュースを見て、自分たちの住んでいるK市のスギ花粉の飛散量に興味を持ちました。次の資料は、K市の30年間における、スギ花粉の飛散量と前年の7,8月の日照時間のデータの一部です。また、図1は、資料をもとに作成した。K市の30年間における、スギ花粉の飛散量のヒストグラムです。なお、K市の30年間における、スギ花粉の飛散量の平均値は2567個でした。①、②に答えなさい。
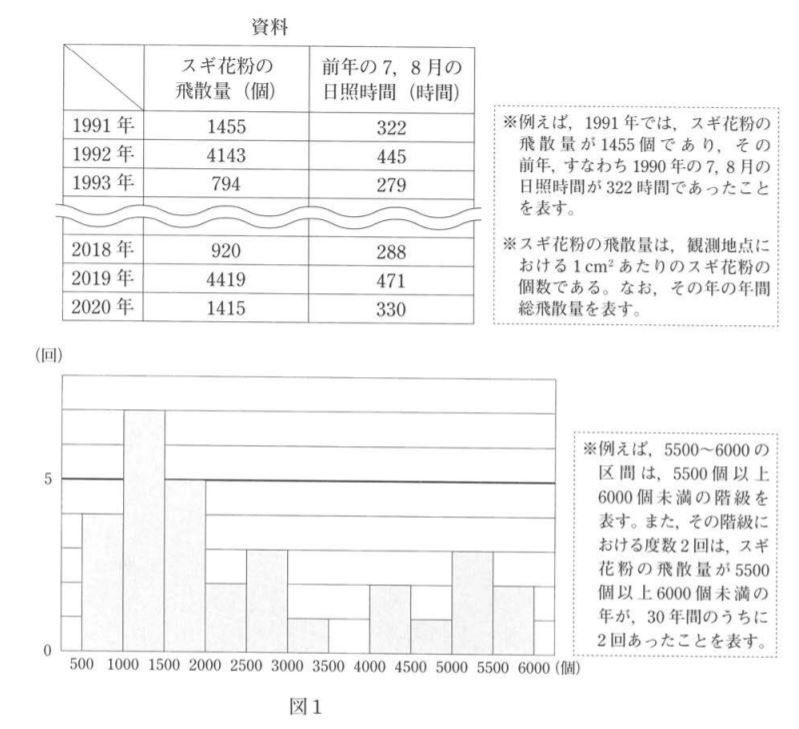
①太郎さんと花子さんは、図1について話しています。<会話Ⅰ>の(1)~(3)に適当な数や階級を書きなさい。

(1)
【答え】3(回)
【解説】平均値が入っているのは2500-3000の階級。度数を数える。
(2)
【答え】1000個以上1500個未満
【解説】一番度数が大きいのは1000-1500の階級
(3)
【答え】1250(個)
【解説】最頻値は1000と1500の平均値を取れば良い
②太郎さんと花子さんは、資料を基に、スギ花粉の飛散量と前年の7,8月の日照時間との関係を調べました。<会話Ⅱ>を読んで、(1)~(3)に答えなさい。

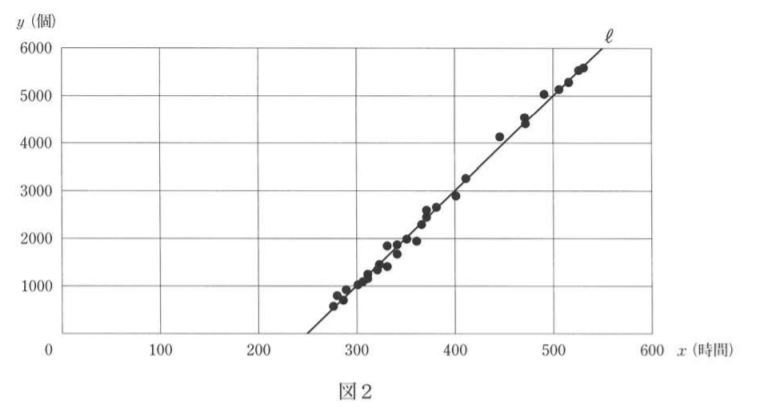
(1)下線部(あ)について、直線ℓの式を求めなさい。
【答え】y=20x-5000
【解説】y=ax+bに代入、a,bについての連立方程式を解く
直線上の点(300,1000)、(400,3000)を代入する
300a+b=1000・・・①
400a+b=3000・・・②
②-①をすると
100a=2000
a=20
これを①に代入し、b=5000
(2)(い)に適当な数を書きなさい。
【答え】2440(個)
【解説】上問の結果にx=372を代入
y=20×372-5000=7440-5000=2440
(3)花子さんが、下線部(う)のように考えた理由について、中央値が入っている階級を示して説明しなさい。
【答え・解説】中央値の入っている階級は1500個以上2000個未満であり、予想した値は中央値より大きいから。
次の図のように、円周上の点A,B,Cを頂点とする△ABCがあり、∠ABCの二等分線と線分ACとの交点をD、円との交点のうち点Bと異なる点をEとします。また、線分AB上に点Fを、EF//CBとなるようにとり、線分EFと線分ACとの交点をGとします。さらに、点Aと点E、点Cと点Eをそれぞれ結びます。①、②に答えなさい。
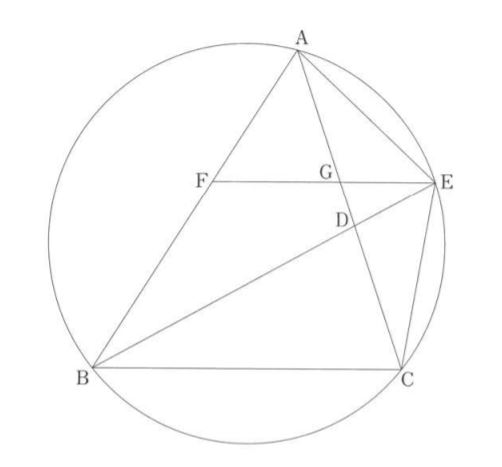
①△ABD∽△ECDを証明しなさい。
【答え・解説】
△ABDと△ECDにおいて、
弧BCに対する円周角は等しいので
∠BAD=∠CED・・・①
対頂角は等しいので
∠ADB=∠EDC・・・②
①、②から
2組の角がそれぞれ等しいので
△ABD∽△ECD
②AB=6cm、BC=5cm、AE=3cmであるとき、(1)~(3)に答えなさい。
(1)線分CEの長さを求めなさい。
【答え】3(cm)
【解説】BEが∠ABCの二等分線であるから∠ABE=∠CBE
よって孤AE=孤CE
したがってAE=CE=3cm
(2)ED:DGを最も簡単な整数比で答えなさい。
【答え】2:1
【解説】相似な三角形を見つけてゆけばよい。
∠ABE=∠DAE・・・①
∠AEB=∠DEA・・・②
①、②より、△AEB∽△DEA・・・③
∠ABE=∠DAE・・・④
∠AEB=∠DEA・・・⑤
④、⑤より、△DEA∽△DGE・・・⑥
③、⑥より△AEB∽△DGE・・・⑦
⑦より
AB:AE=DE:DG=6:3=2:1
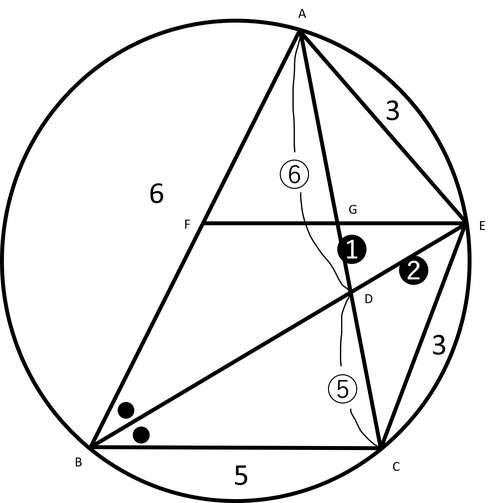
(3)線分AFの長さを求めなさい。
【答え】27/11(cm)
【解説】右図も参照ください。
∠ABE=∠CBEよりBA:BC=AD:CD=6:5・・・①
△ADE∽△BDCよりAE:BC=ED:CD=3:5・・・②
(2)よりED:DG=2:1・・・③
②、③よりCD:DG=10:3・・・④
①、④よりAD:DG=12:3・・・⑤
⑤よりAG:DG=9:3・・・⑥
これらよりAG:DG:CD=9:3:10
よってAG:AC=9:22
FG//BCよりAF:FB=AG:AC
すなわちx:6=9:22
x=27/11
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています!
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…?」とご質問いただくことも多いですが、ご安心ください!家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです!
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

