愛知県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 愛知県の公立高校入試情報はこちら

【愛知A】大問1

問題文

次の(1)から(10)までの問いに答えなさい。
(1) 8+(-3)×2を計算しなさい。

(2) (2x-3)/6 – (3x-2)/9を計算しなさい。

(3) 5x²÷(4xy)²×32xy² を計算しなさい。

(4) (√5-√3)(√20+√12)を計算しなさい。

(5) 方程式5(2-x)=(xー4)(x+2)を解きなさい。

(6) 次のアからエまでの中から、yがに反比例するものを全て選んで、そのかな符号を書きなさい。
ア 1辺の長さが㎝である立方体の体積y㎝³
イ 面積が35㎝²である長方形のたての長さ㎝と横の長さy㎝
ウ 1辺の長さがx㎝である正方形の周の長さy㎝
エ 15㎞の道のりを時速x㎞で進むときにかかる時間y時間

(7) 6人の生徒が1か月間に読んだ本の冊数を少ない順に並べると、右のようになった。6人の生徒が1か月間に読んだ本の冊数の平均値と中央値が同じとき、aの値を求めなさい。

(8) A、Bは関数y=22のグラフ上の点で、座標がそれぞれー3、6のとき、直線ABに平行で原点を通る直線の式を求めなさい。

(9) 体積の等しい2つの円柱P、Qがあり、それぞれの底面の円の半径の比は3:5である。このとき、円柱Qの高さは、円柱Pの高さの何倍か、求めなさい。

(10) 図で、四角形ABCDはAD//BCの台形、Eは線分ACとDBとの交点である。AD =6㎝、AE =3㎝、EC=7㎝のとき、BCの長さは何㎝か、求めなさい。

解答・解説

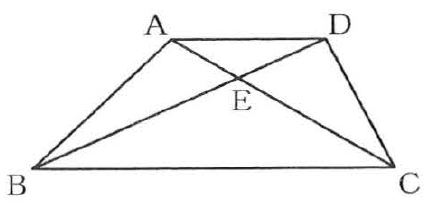
(1) 8+(-3)×2=8+(-6)=8-6=2

(2) ｛3×(2x-3)｝/18 -｛2×(3x-2)｝/18={(6x-9)-(6x-4)}/18=-5/18

(3) 5x²÷(4xy)²×32xy²=5x²×1/16x²y²×32xy²=10x

(4) (√5-√3)(√20+√12)=√100+√60-√60-√36=√100-√36=10-6=4

(5)
5(2-x)=(x-4)(x+2)
10-5x=x²+2x-4x-8
x²-2x-8=10-5x
x²+3x-18=0
(x+6)(ｘ-3)=0
x=-6,3

(6) イ・エ
ア・・・y=x³
イ・・・y=35/x
ウ・・・ý=4x
エ・・・y=15/x

(7) a=8
平均値・・・(31+a)/6
中央値・・・(5+a)/2
(31+a)/6=(5+a)/2
31+a=3×(5+a)
31+a=15+3a
2a=16
a=8

(8) y=3x
点Aの座標(-3,9)
点Bの座標(6,36)
2点A・Bを通る直線の傾きは「yの増加量/xの増加量」で求められるため、
(36-9)/{6-(-3)}=27/9=3
原点を通る直線の式はy=axで表せるため、求める式はy=3x

(9) 9/25倍
円柱の体積の公式はπr²h(円周率π、半径r、高さh)
円の半径の比が3：5ということは、体積比は3²：5²=9：25
円柱P・Qの体積は等しいから円柱Qの高さは円柱Pの高さの9/25倍になる。

(10) 14㎝
△AEDと△CEBについて。
∠AED=∠CED(対頂角)・・・➀
∠EAD=∠ECB(錯角)・・・②
➀②より△AED∽△CEB
EA：EC=3：7なので、
AD：CB=3：7
6：BC=3：7(AD=6㎝のため)
3×BC=42
BC=42/3
BC=14

大問2

問題文

次の(1)から(3) までの問いに答えなさい。

(1) 図で、Oは原点、点A、B、C、Dの座標はそれぞれ(0,6)、(-3,0)、(6,0)、(3,4)である。また、Eは軸上を動く点である。△ABEの面積が四角形ABCDの面積の1/2倍となる場合が2通りある。このときの点Eの座標を2つとも求めなさい。

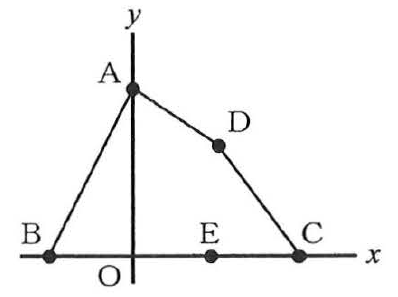
(2) 次の文章中の[Ⅰ]にあてはまる式を書きなさい。また、[Ⅱ]にあてはまる数を書きなさい。
1から9までの9個の数字から異なる3個の数字を選び、3けたの整数をつくるとき、
つくることができる整数のうち、1番大きい数をA、1番小さい数をBとする。例えば、2,、4、 7を選んだときは、A=742、B= 247となる。
A-B=396となる3個の数字の選び方が全部で何通りあるかを、次のように考えた。
選んだ3個の数字を、a、b、c(a>b>c)とするとき、A-Bをa、b、 cを使って表すと、 [Ⅰ]となる。この式を利用することにより、A-B=396となる3個の数字の選び方は、全部で[Ⅱ]通りであることがわかる。

(3) A地点とB地点は直線の道で結ばれており、その距離は18 kmである。
6人がA地点からB地点まで移動するために、運転手を除いて3人が乗車できるタクシーを2台依頼したが、 1台しか手配することができなかったので、次のような方法で移動することにした。

6人を3人ずつ、第1組、第2組の2組に分ける。
・ 第1組はタクシーで、第2組は徒歩で、同時にA地点からB地点に向かって出発する。
・第1組は、A地点から15km離れたC地点でタクシーを降り、降りたらすぐに徒歩でB地点に向かって出発する。
・タクシーは、C地点で第1組を降ろしたらすぐに向きを変えて、A地点に向かって出発する。
・第2組は、C地点からきたタクシーと出会った地点ですぐにタクシーに乗り、タクシーはすぐに向きを変えてB地点に向かって出発する。

タクシーの速さは毎時36 km、第1組、第2組ともに歩く速さは毎時4kmとするとき、次の①、②の問いに答えなさい。
ただし、タクシーの乗り降りやタクシーが向きを変える時間は考えないものとする。

➀第1組がA地点を出発してからx分後のA地点からの距離をykmとするとき、A地点を出発してからB地点に到着するまでのxとyの関係を、グラフに表しなさい。
②第2組がタクシーに乗ったのはA地点を出発してから何分後か、求めなさい。

解答・解説

(1) (2,0)、(-8,0)
まず、点Dを通り線分ACに平行な直線は、y=-x+7
この直線とx軸との交点はD´(7,0)
このとき△ACD=△ACD´なので、
四角形ABCD=△ACD´である。
よって、線分BD´の中点が求める座標の1つである。
(-3+7)÷2=2なので、(2,0)が正解の1つになる。
またもう一つの点は点Bに関してこの点(2,0)と対称な点になるので、(-8,0)

(2) Ⅰ 99(a-c)、Ⅱ 15通り
Ⅰ
A=100a+10b+c、B=100c+10b+aと表せるため、
A-B=(100a+10b+c)-(100c+10b+a)=99a-99c=99(a-c)

Ⅱ
99(a-c)=(396/4)×(a-c)と表せるため、
A-B=396となるのは、a-c=4となる場合である。
その組み合わせは、
(a,c)=(5,1)、(6,2)、(7,3)、(8,4)、(9,5)
の5通りであり、その組み合わせそれぞれについてbの選び方が3通りずつある。
よって、5×3=15通り

(3) ➀下図、②45分後

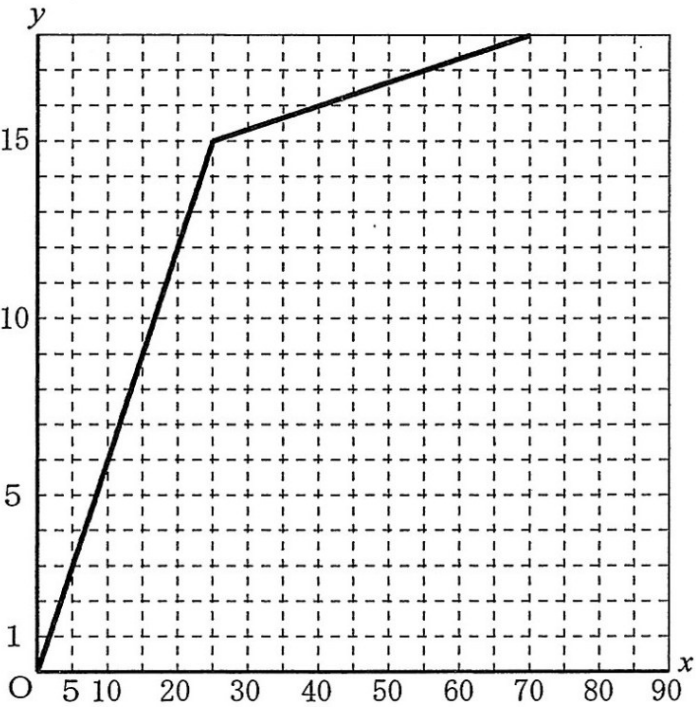
➀、②
第1組、第2組、タクシーの動きは、次のようになる。

大問3

問題文

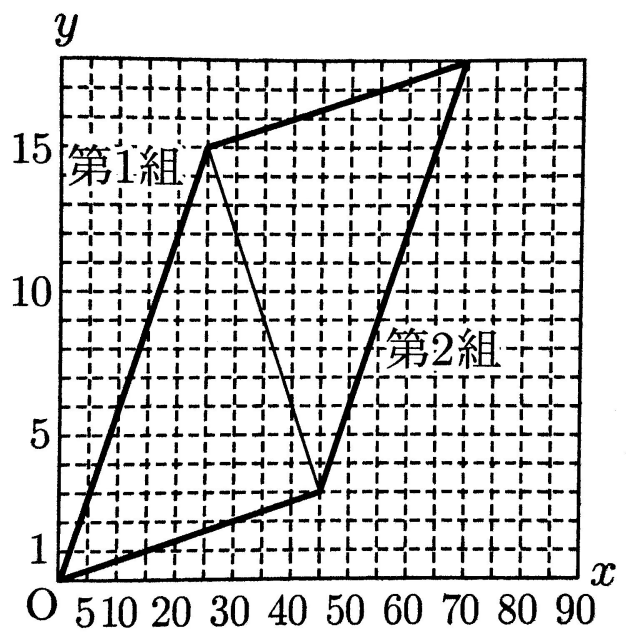
次の(1) から(3) までの問いに答えなさい。
ただし、答えは根号をつけたままでよい。

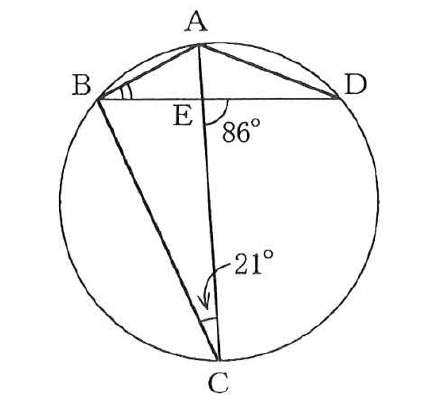
(1) 図で、A、B、C、Dは円周上の点で、線分ACは∠BADの二等分線である。また、Eは線分ACとBDとの交点である。∠DEC=86°、∠BCE=21°のとき、∠ABEの大きさは何度か、求めなさい。

(2) 図で、四角形ABCDは長方形であり、Eは長方形ABCDの内部の点で、∠BAE=45°である。
四角形ABCD、△ABE、△AEDの面積がそれぞれ80㎝²、10㎝²、16㎝²のとき、次の①、②の問いに答えなさい。

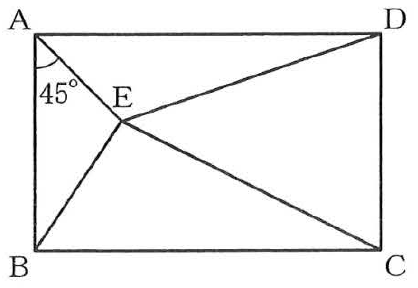
➀△DECの面積は何㎝²か、求めなさい。
②辺ABの長さは何㎝か、求めなさい。

(3) 図で、立体ABCDEは辺の長さが全て等しい正四角すいで、AB=4㎝である。Fは辺BCの中点であり、G、 Hはそれぞれ辺AC、 AD上を動く点である。
3つの線分EH、HG、GFの長さの和が最も小さくなるとき、次の➀、②の問いに答えなさい。

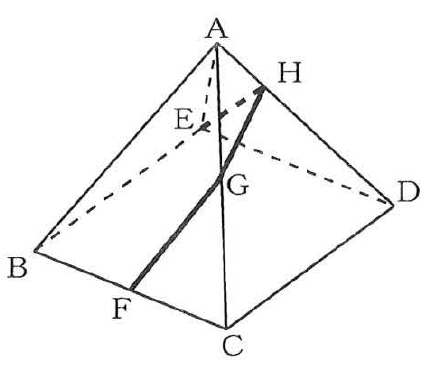
➀線分AGの長さは何cmか、求めなさい。
②3つの線分EH、HG,、GFの長さの和は何cmか、求めなさい。

解答・解説

(1) 29度
∠EBC=86°-21°=65°
同じ弧CDの円周角なので、∠EBC=∠EAD=65°
線分ACは∠BADの2等分線なので、∠BAD=∠EAD×2=65°×2=130°・・・➀
また、同じ弧ABの円周角なので、∠ADB=∠ACB=21°・・・②
➀②より、∠ABE=180°-(∠BAD+∠ADB)=180°-(130°+21°)=29°

(2) ➀30㎝²、②5√2㎝
➀
△ABE+△DEC=長方形ABCD×1/2=80×1/2=40(㎝²)
よって、10+△DEC=40より、
△DEC=40-10=30(㎝²)
②
△AED+△BEC=40
16+△BEC=40
△BEC=40-16=24(㎝²)
また、点Eから辺ABに引いた垂線の足をHとすると、
AH：HB=△AED：△EBC=16：24=2：3
△AHEは直角二等辺三角形で、
△AHE=△ABE×2/(2+3)=10×2/5=4(㎝²)・・・➀
△AHE=AH×HE×1/2=AH²×1/2・・・②
➀②より、
AH²×1/2=4
AH²=8
AH=2√2 (AH>0のため)
また、HB=AH×3/2=2√2×3/2=3√2
よって、AB=AH+HB=2√2+3√2=5√2

(3) ➀4/3㎝、②2√13㎝
記載した展開図で考える。
➀
AH//BFであるから、平行線と線分の比より、
AH：BF=EA：EB=1：2
△GHA∽△GFC、△GHA：△GFC=1：2であるから、
AG=AC×1/(1+2)=4×1/3=4/3(㎝)
②
AB=AC=AEより、∠FCE=90°(円周角と直径の関係)
△EBCについて、三平方の定理より、
EC=√(EB²-BC²)=√(8²-4²)=√(64-16)=√48=4√3
△EFCについて、三平方の定理より、
EF=√(FC²+EC²)=√{2²+(4√3)²}=√(4+48)=√52=2√13(㎝)

【愛知B】大問1

問題文

(1)6÷(-2)-(-7)

(2)2(6x-8y)+3(5y-4x)

(3)(x+5)(x-2)-3(x-3)

(4)(√5+√2)²-(√5-√2)²

(5)方程式 (2x+1)²-3x(x+3)=0

(6)消しゴムがy個あり、生徒x人に3個ずつ配ったら余った。
この数量の関係を不等式に表しなさい。

(7)箱の中に1から9までの数字が書かれた玉が1個ずつ入っている。中を見ないで、この箱の中から玉を1個ずつ取り出すとき、6の約数が書かれた玉が出る確率を求めなさい。

(8)横の長さが8cm、たての長さが6cmの長方形のカードがある。このカードと同じカードを同じ向きにすき間のないように並べて、なるべく小さな正方形をつくるとき、カードは何枚必要か、求めなさい。

(9)Aは2点(-3，-8),(1,4)を通る直線上の点で、x座標が3である。
このとき、点Aのy座標を、求めなさい。

(10)次のアからエまでの立体のうち、体積が最も大きいものはどれか、そのかな符号を答えなさい。
ア 1辺が1cmの立方体
イ 底面の正方形の1辺が2cm、高さが1cmの正四角すい
ウ 底面の円の直径が2cm、高さが1cmの円すい
エ 底面の円の直径が1cm、高さが1cmの円柱

解答

(1) 4
6÷(-2)-(-7)=-3+7 =4

(2) -y
2(6x-8y)+3(5y-4x) = 12x-16y+15y-12x = -y

(3)(x+1)(x-1)
(x+5)(x-2)-3(x-3) = x²-2x+5x-10-3x+9 = x²-1 = (x+1)(x-1)

(4) 4√10
(√5+√2)²-(√5-√2)² = 5+2√10+2-(5-2√10+2) = 5+2√10+2-5+2√10-2 = 4

(5) (5±√21)/2
(2x+1)²-3x(x+3)=0 = 4x²+4x+1-3x²-9x=0 = x²-5x+1=0
2次方程式の解の公式 (-b±√b²-4ac)/2a より
(5±√(-5)²-4)/2 = (5±√21)/2

(6) y＞3x
y個をx人に3個ずつ配ると余る よって y＞3x

(7) 4/9
6の約数は 1.2.3.6 の4つ よって 4/9

(8) 12枚
8と6の最小公倍数は24 たて・横どちらも24cmにすると
横に3枚、たてに4枚並べられる 3×4 =12 よって 12枚

(9) y=10
傾きはyの増加量÷xの増加量であり
xの増加量は 1-(-3)=4 yの増加量は 4-(-8)=12 傾き=12/4=3
y=3x+b (-3，-8)より -8=-9+b b=1
y=3x+1 xが3のとき y=9+1=10 よって y=10

(10) イ
ア 1×1×1=1cm³
イ 2×2×1÷3=4/3cm³
ウ 1×1×3.14×1÷3=3.14/3cm³
エ 0.5×0.5×3.14=3.14/4cm³ よって イ

大問2

問題文

次の(1)から(3)までの問いに答えなさい。

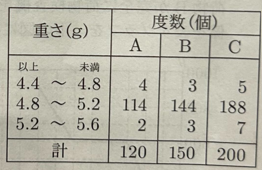
(1)表は、ある工場で使われている、ねじを作る機械A,B,Cの性能を確かめるために、それぞれの機械によって1時間で作られたねじの一本あたりの重さを度数分布表にまとめたものである。なお、この工場では、4.8g以上5.2g未満のねじを合格品としている。
表からわかることについて正しく述べたものを、次のアからケまでの中から全て選んで、そのかな符号を書きなさい。

ア 1時間あたりで、合格品を最も多く作ることができる機械は、A である。
イ 1時間あたりで、合格品を最も多く作ることができる機械は、Bである。
ウ 1時間あたりで、合格品を最も多く作ることができる機械は、Cである。
エ 1時間あたりで、合格品を作る割合が最も高い機械は、A である。
オ 1時間あたりで、合格品を作る割合が最も高い機械は、Bである。
力 1時間あたりで、合格品を作る割合が最も高い機械は、Cである。
キ 1時間あたりで、作ったねじの重さの平均値が 5.0gより小さくなる機械は、A である。
ク 1時間あたりで、作ったねじの重さの平均値が 5.0gより小さくなる機械は、Bである。
ケ 1時間あたりで、作ったねじの重さの平均値が 5.0gより小さくなる機械は、Cである。

(2)図で、Oは原点、A,Bは関数y=1/2x²のグラフ上の点で、x座標はそれぞれ -2,4である。
また、C,Dは関数y=-1/4x²のグラフ上の点で、点Cのx座標は点Dのx座標より大きい。四角形ABCDが平行四辺形のとき、点Dのx座標を求めなさい。

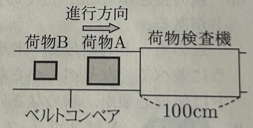
(3)図は、荷物A，Bが矢印の方向にベルトコンべア上を、毎秒20cm の速さで荷物検査機に向かって進んでいるところを、真上から見たものである。荷物検査機と荷物A，Bを真上から見た形は長方形で，荷物検査機の長さは100cmである。荷物Aが荷物検査機に入り始めてからxcm進んだときの，真上から見て荷物検査機に入って見えない荷物A,Bの面積の合計をycm²とする。下の図は、荷物Aが荷物検査機に入り始めてから，荷物Bが完全に荷物検査機に入るまでのxとyの関係をグラフに表したものである。
このとき、次の(1),(2)の問いに答えなさい。

①荷物Bが荷物検査機に完全に入ってから、荷物Bが完全に荷物検査機を出るまでのxとyの関係を表すグラフを、下の図に書き入れなさい。
②荷物検査機は、荷物が完全に荷物検査機に入っているときに、荷物の中身を検査できる。
荷物Bの中身を検査できる時間は何秒間か、求めなさい。

解答

(1) ウ、オ、キ
ア～ウ 合格品は A114個 B144個 C188個 ウ
エ～カ 合格率はそれぞれ
A 114/120 = 570/600 B 144/150 = 576/600 C 188/200 = 564/600 オ
キ～ケ 階級値はそれぞれ4.6g、5.0g、5.4g
平均を5.0gとして、4.6gの個数と5.4gの個数を考えると
A 4.6g → 4個 5.4g → 2個 4.6gが2個多い
B 4.6g → 3個 5.4g → 3個 4.6gと5.4gは同数
C 4.6g → 5個 5.4g → 7個 5.4gが2個多い
よって、作ったねじの重さの平均値が5.0gより小さくなるのは キ

(2) x=-5
x座標 -2と4をそれぞれy=1/2x²に代入すると
(x,y)=(-2,2)と(4,8)となる
変化の割合=(yの増加量)/(xの増加量)=(8-2)/(4-(-2))=6/6=1
平行四辺形なのでDCの傾きも1
y=ax²においてxがmからnに増加するときの変化の割合はa(ｍ+n)となる
Dのx座標をmとすると、Cのx座標は(m+6)
y= -1/4x²を用いて、 -4/1(m+m+6)=1 2m+6=-4 2m=-10 m=-5 よって x=-5

(3) ①

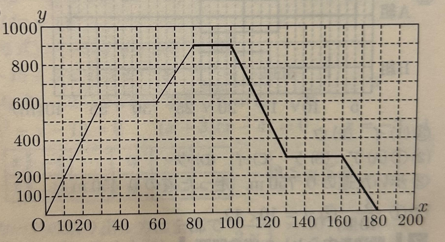
xが30になったときAは全て荷物検査機に入る。
これによりAの長さは30cmと分かり、グラフよりAの面積が600cm²と分かる。
xが30から60になるまではyに変化が無いことからABの間隔は30cmと分かる。
そこからさらにxが20増えたところ(x=80)でBが完全に隠れるため、Bの長さは20cmと分かり、yが300増えているためBの面積は300cm²と分かる。
Aの右端からBの左端までの長さは80cmとなる。
Bが完全に隠れてから20cm進むまで(x=100)はABともに完全に隠れている為yに変化はない。
そしてAが荷物検査機から出始めて、30cm進む(x=130)とAは完全に荷物検査機から出るため、xが100から130に変わる間にyが600下がる。
そこから30cm進むまで(x=160)はyに変化はない。その後Bが荷物検査機から出始めて、20cm進むと(x=180)Bも完全に荷物検査機から出るため、xが160から180に変わる間にyが300下がる。

② 4秒間
荷物Bが完全に隠れているのはxが80から160までの80cm
毎秒20cmずつ動いているので、80÷20=4 よって 4秒間

大問3

問題文

次の(1)から(3)までの問いに答えなさい。
ただし、答えは根号をつけたままでよい。

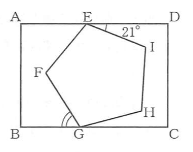
(1)図で、四角形ABCDは長方形、五角形EFGHIは正五角形であり、点Ｅ,Ｇはそれぞれ辺AD,BC上にある。∠DEI=21°のとき、∠FGBの大きさは何度か、求めなさい。

(2)図で、立体ABCDEFGHは立方体、Iは辺AB上の点で、AI：IB=2：1であり、Jは辺CGの中点である。AB=6cmのとき、次の①,②の問いに答えなさい。

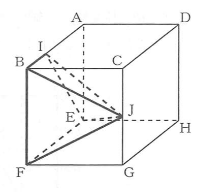
①線分IJの長さは何cmか、求めなさい。
②立体JIBFEの体積は何cm³か、求めなさい。

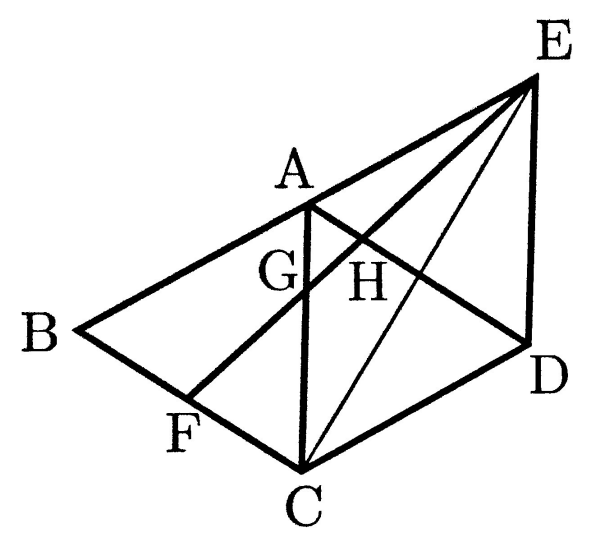
(3)図で、C,Dは線分ABを直径とする円Oの周上の点であり、Eは直線ABとDCとの交点で、DC=CE,AO=BEである。円Oの半径が4cmのとき、次の①,②の問いに答えなさい。

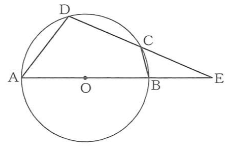
①△CBEの面積は、四角形ABCDの面積の何倍か、求めなさい。
②線分ADの長さは何cmか、求めなさい。

解答

(1) 51°
n角形の内角の和は180×(n-2)なので五角形の内角の和は540°
正五角形なので1つの角は108° これにより∠AEFは180-(21+108)=51°
点Fを通る辺AD・辺BCに平行な補助線を引き錯角を利用して求める。

(2) ① 7cm
面BFGCと辺ABは垂直なので△IBJは直角三角形である。
三平方の定理(1：2：√5)より BJは3√5cm
三平方の定理より IJ²=IB²+BJ²なので、IJ²=2²+(3√5)² = 4+45 =49 IJ²=49 IJ=7 よって 7cm

② 48cm³
底面のBIEFは台形なので面積は(2+6)×6÷2=24cm²
この四角すいの高さは6cmなのでJIBFEの体積は24×6÷3=48 よって 48cm³

(3) ① 1/5倍
問題文より、DC=CE AO=BEが分かっており
AOは円の半径であるため、AO=OB=BE=4cmとなる。

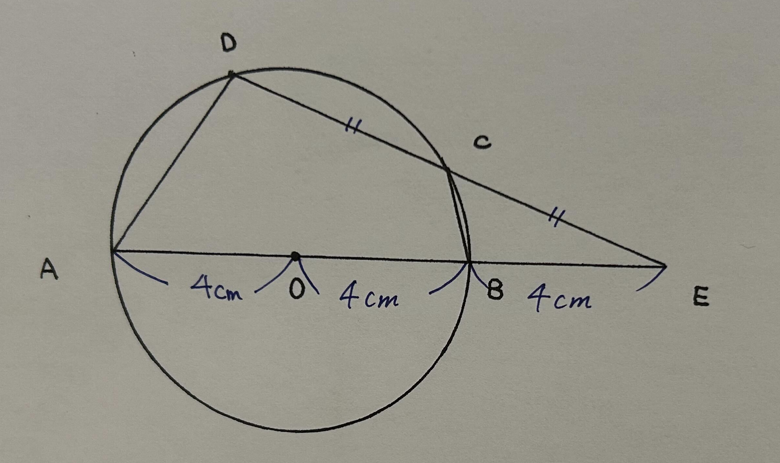
補助線ODを引いて、中点連結定理を使う。
※中点連結定理とは、三角形の2辺の中点を結んだとき「底辺が平行」「長さが半分になる」

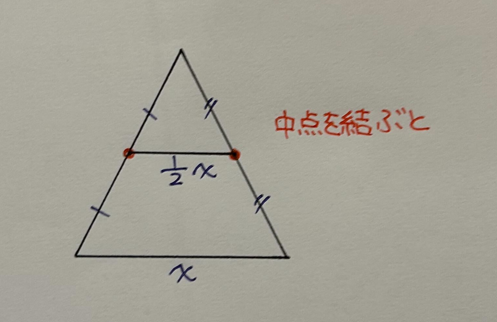
↓ODに補助線を引く。ODは半径なので4cmとなる。
DC=CE,OB=BEとなるため、中点連結定理によりCB=2cmとなる。

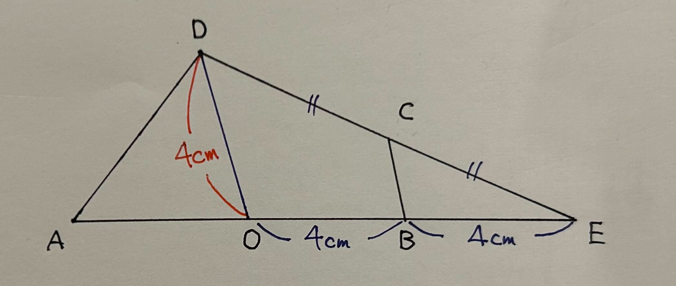
△CBEと△DOEは相似比1：2の相似となる。

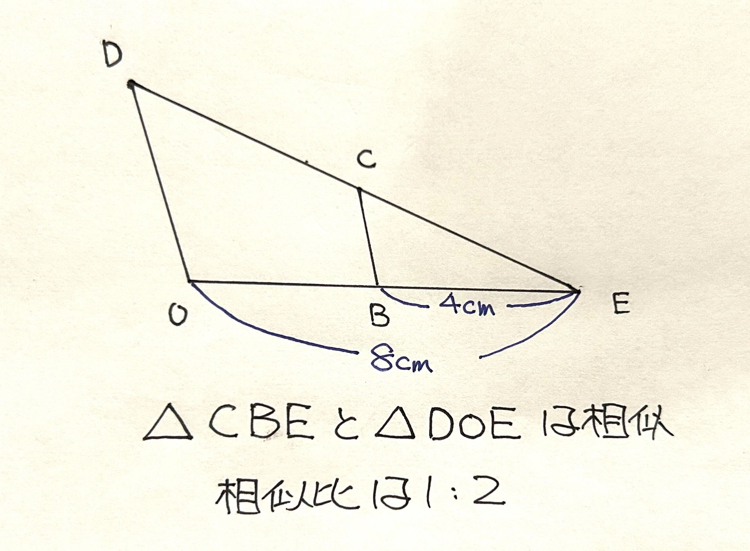
相似比がm：nならば面積比はm²：n²となる。
よって、△CBEの面積をaとすると、△DOEの面積は4aとなる。

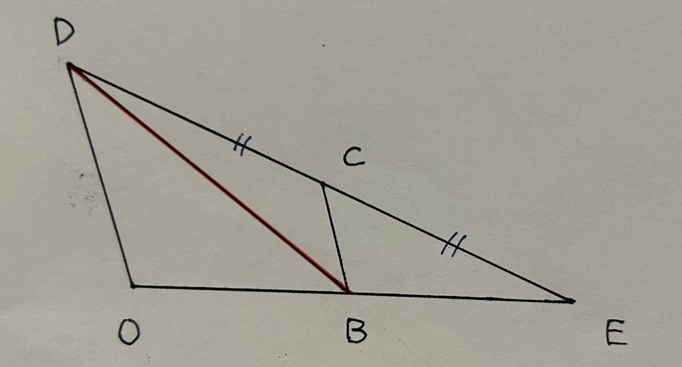
△CBEと△CBDは底辺の長さが同じであるため、△CBEと△CBDは△BEDを二等分している。
よって、△CBEと△CBDの面積は同じになる。
△CBE=△CBD=aと表せる。△DOEの面積が4aのため
4a-a-a=2a で△OBEの面積が2aと表せる。

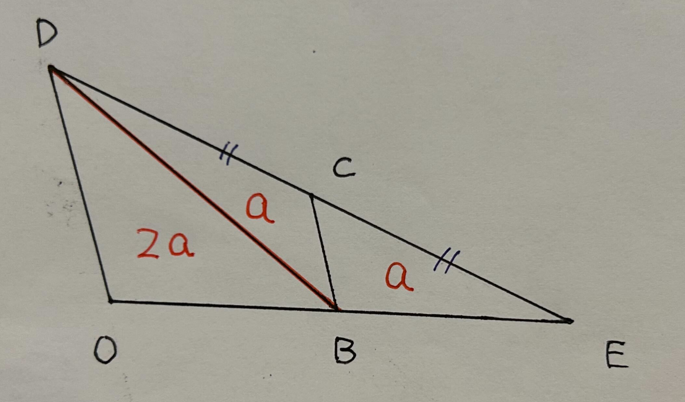
△OBDと△OADは底辺の長さが同じであるため、△OBDと△OADは△BADを二等分している。
よって、△OBDと△OADの面積は同じになる。
△OBD=△OAD=2a
これらにより、四角形ABCDの面積は5a、△CBEの面積はaと分かる。
よって、△CBEの面積は四角形ABCDの面積の1/5倍となる。

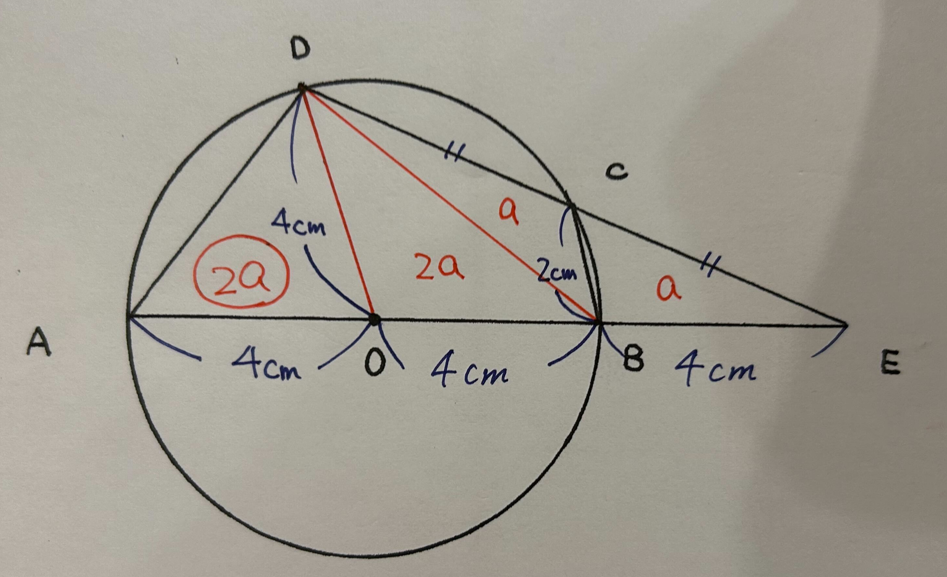
② 2√6cm
円に内接する四角形の向かい合う角の和は180°になり、
∠OADをa°としたとき、∠BCDは(180-a)°となるため∠BCEはa°となる。

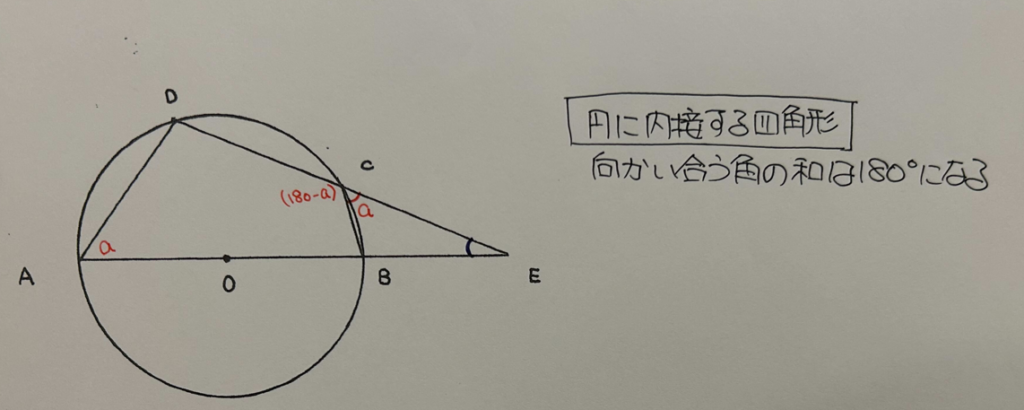
△CBEの向きを変えて考えてみると、 △AEDと△CBEは2組の角の大きさが等しいため相似であることが分かる。

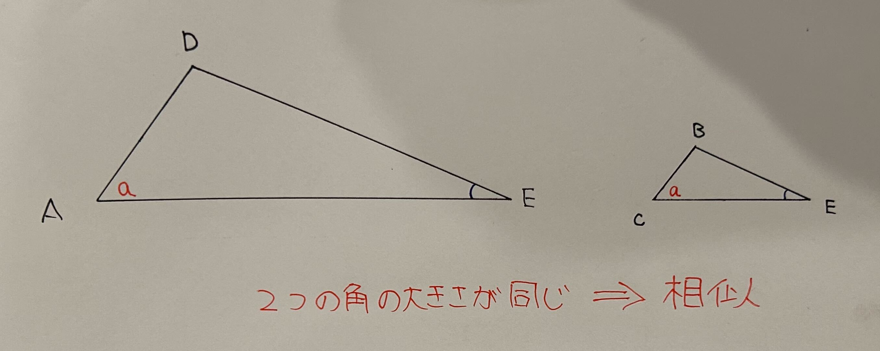
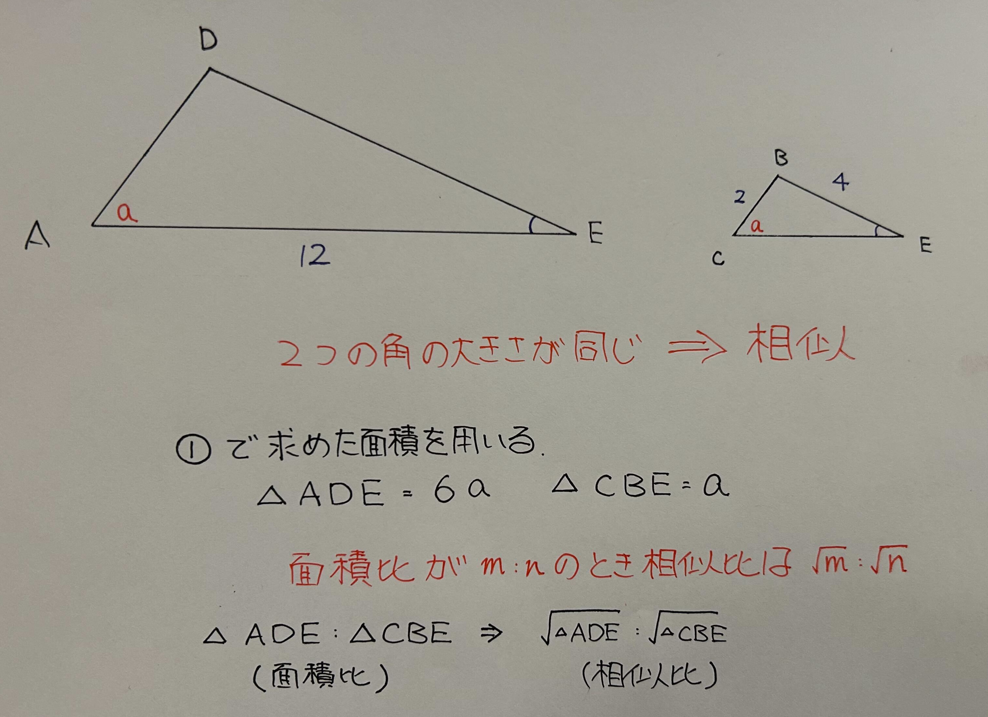
先ほど①で求めた面積を用いて考えてみると、
△AEDの面積は6a、△CBEの面積はaとなる。
△AEDと△CBEの面積比は6：1
相似のとき、面積比がm：nならば、相似比は√m：√nとなる。
△AEDと△CBEの相似比は、√6：1
よって、AD：CB=√6：1
CB=2と分かっているためAD=2√6となる。

 愛知県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！

教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！

受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。