岐阜県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 岐阜県の公立高校入試情報はこちら

大問1

問題文

(1)6-4×(-2)

(2)3(-x+y)-(2x-y)

(3)x=5+√3、y=5-√3のときの式x²+2xy+y²の値

(4)2個のさいころを同時に投げるとき、出る目の数の積が5の倍数になる確率

(5) 連立方程式
｛5x+2y=4
｛3x-y=9

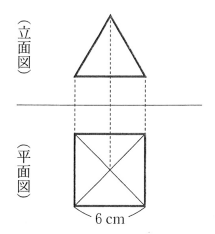
(6)図は、正四角すいの投影図である。立面図が正三角形、平面図が一辺の長さが6cmの正方形であるとき、この正四角すいの体積を求めなさい。

解答・解説

(1) 14
6-4×(-2)=6+8=14

(2) -5x+4y
3(-x+y)-(2x-y)=-3x+3y-2x+y=-5x+4y

(3) 100
x²+2xy+y²=(x+y)²=(5+√3+5-√3)²=10²=100

(4) 11/36
出目a 、 出目b a×bは最大36 5の倍数は 、 5.10.15.20.25.30
5.10.15.20.30 → a,bそれぞれ逆の目でも成立する
25 → a,bともに5のとき
よって 11/36

(5) x=2 , y=-3
｛5x+2y=4 ・・・①
｛3x-y=9 ・・・②
②を移項する → y=3x-9・・・②’
②’を①に代入する → 5x+2(3x-9)=4
5x+6x-18=4 = 11x=22 = x=2
x=2を②に代入する
6-y=9 = y=-3
よって x=2 , y=-3

(6) 36√3㎤
四角錐の体積=底面積×高さ÷3
立面図より 斜辺6 底辺3 三平方の定理 = 1：2：√3 により
高さは3√3 6×6×3√3÷3=36√3
よって 36√3㎤

大問2

問題文

2次方程式 x²+ax-8=0について次の(1),(2)の問いに答えなさい。

(1)a=-1のとき、2次方程式を解きなさい。

(2)x=1が2次方程式の1つの解であるとき
(ア)aの値を求めなさい。
(イ)他の解を求めなさい。

解答・解説

(1) (1±√33)/2
a=-1 を x²+ax-8=0に代入するとx²-x-8=0
解の公式 (-b±√b²-4ac)/2aにより、(1±√1+32)/2 =(1±√33)/2

(2)
(ア) a=7
1²+a=8 = a=7
(イ) -8
x²+7x-8=0 = (x-1)(x+8)=0 = x=1,-8 よって、他の解は -8

大問3

問題文

A中学校のバスケットボール部は、ある日の練習で、全ての部員がそれぞれシュートを5回ずつ行い、成功した回数を記録した。この図は、その記録をもとに、成功した回数別の人数をグラフに表したものである。次の(1)～(3)の問いに答えなさい。

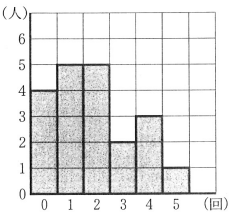
(1)図から、A中学校のバスケットボール部の部員の人数を求めなさい。

(2)図から、成功した回数の平均値を求めなさい。

(3)バスケットボール部に入部を予定している花子さんも、別の日にシュートを5回行い、成功した回数を記録した。花子さんの記録を図に表された記録に加え、成功した回数の平均値と中央値を求めると、2つの値が等しくなった。花子さんの成功した回数を求めなさい。

解答・解説

(1)20人
4+5+5+2+3+1=20

(2)1.9回
成功数 (0)+(1×5)+(2×5)+(3×2)+(4×3)+(5×1)=38
成功数÷人数=38÷20=1.9 よって 1.9回

(3)4回
中央値=中央にある2つの値の平均
0,0,0,0,1,1,1,1,1,2,2,2,2,2,3,3,4,4,4,5 「2」と「2」の平均=2 よって中央値=2
花子さんの成功数が0～5回いずれの場合も中央値は2のままであり、

平均値が2になるのは21×2で成功数が42のとき。

よって42-38となり花子さんの成功数は 4回 となる。

大問4

問題文

図のような台形ABCDがある。点P,Qが同時にAを出発して、Pは秒速2cmで台形の辺上をAからBまで動き、Bで折り返してAまで動いて止まり、Qは秒速1㎝で台形の辺上をAからＤを通ってＣまで動いて止まる。P,QがＡを出発してからx秒後の△APQの面積をycm²とする。(1)～(4)の問いに答えなさい。

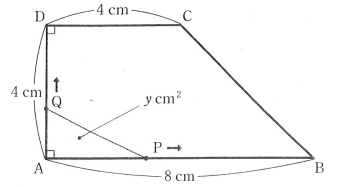
(1)表中のア、イに当てはまる数を求めなさい。

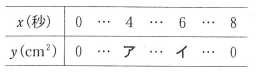
(2)xの変域を次の(ア),(イ)とするとき、yをxの式で表しなさい。
(ア) 0≦x≦4のとき
(イ)4≦x≦8のとき

(3)xとyの関係を表すグラフをかきなさい。(0≦x≦8)

(4)△APQの面積と、台形ABCDから△APQを除いた面積の比が、3：5になるのは、P,QがAを出発してから何秒後と何秒後であるかを求めなさい。

解答・解説

(1)ア 16 , イ 8
ア 4秒後のAPの長さは8cm、AQの長さは4cm 8×4÷2=16 よって 16
イ 6秒後のAPの長さは4cm、QはDC上を平行移動しているため、高さは4cmのまま
4×4÷2=8 よって 8

(2)
(ア) x²
底辺は2x、高さはxとなるためy=2x×x÷2 よって y=x²となる

(イ)-4x+32
底辺は往復16cm²から2xを引いた(16-2x)、高さは4cmで固定となるため
y=(16-2x)×4÷2 よって y=-4x+32となる

(3)

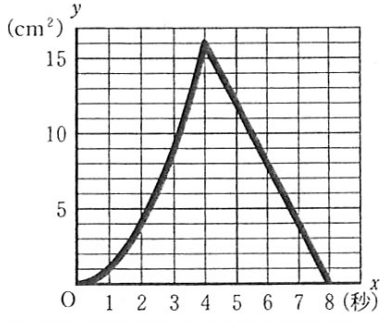
xが0～4まではy=x²のグラフとなり
xが4～8まではy=-4x+32のグラフとなる

(4) 3秒後 , 5.75秒後
台形ABCDの面積は(4+8)×4÷2=24
△APQと台形ABCDから△APQを除いた部分の比が3：5のとき、△APQの面積は
台形ABCDの面積の3/8となる
24×(3/8)=9 9cm²

(2)で求めた2つの式に代入する
①y=x² = 9=x² x=3
②y=-4x+32 = 9=-4x+32 = 4x=23 = x=23/4 =5.75 よって 3秒後と5.75秒後

大問5

問題文

図の△ABCで、点Dは∠ABCの二等分線と辺ACとの交点である。また、点Eは線分BDの延長線上の点で、CD=CEである。次の(1),(2)の問いに答えなさい。

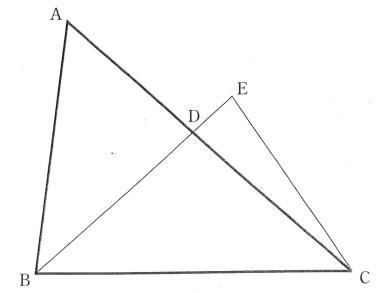
(1)△ABD∽△CBEであることを証明しなさい。

(2)AB=4cm、BC=5cm、CA=6cmのとき
(ア)CEの長さを求めなさい。
(イ)△ABDの面積は、△CDEの面積の何倍であるかを求めなさい。

解答・解説

(1)仮定法
仮定から、∠ABD=∠CBE・・・①
CD=CEなので△CDEは二等辺三角形で∠CDE=∠CEDと分かる・・・②
対頂角の関係から、∠CDE=∠ADBと分かる・・・③
②、③より∠CED=∠ADBとなる・・・④
①、④より2組の角が等しいため △ABD∽△CBEといえる

(2)
(ア)10/3
角の二等分線の性質から、BA：BC=AD：CDが成立する
CEの長さをxとすると、問題文よりCDの長さもxとなり、ADの長さは(6-x)となる
BA：BC=AD：CDを使うと、
4：5=(6-x)：xとなる → 4×x=5×(6-x) = 4x=30-5x = 9x=30 = x=30/9 x=10/3

(イ)16/5倍
AD：CD=4：5なので、△ABCの面積をyとすると△ABDは4/9y △BCDは5/9yとなる
△ABDと△CBEは相似で相似比が4：5となるため、面積比は16：25となる
△ABDを4/9yとすると△CBEは、
4/9y：△CBE=16：25 = 16×△CBE=100/9y = △CBE=100/9y×1/16=25/36yとなる
△CDE=△CBE-△BCD = 25/36y-5/9y = 5/36y
△ABDは4/9y , △CDEは5/36y △ABDを16/36yと考えると△ABDは△CDEの16/5倍となる

大問6

問題文

大きな白い紙に、正方形の形に並ぶように連続した自然数を書いていく。まず、1回目の作業として、1のみを書き、以後、次の作業を繰り返し行う。

【作業】すでに正方形の形に並んでいる自然数の下側に1行、右側に1列を加え、再び正方形の形に並ぶように新たに自然数を書く。自然数は、前の作業で書いた自然数の続きから、まず左下から右下へ、次に右下から右上へ小さい順に書く。

次の図は、1回目から3回目までの作業後の結果である。例えば、3回目の作業については、新たに書いた自然数の個数は5個であり、正方形の右下に書いた自然数は7である。

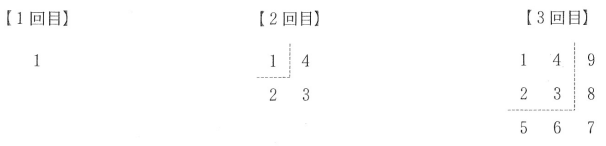
次の(1)～(3)の問いに答えなさい。

(1)5回目の作業について、
(ア)新たに書く自然数の個数を求めなさい。
(イ)正方形の右下に書く自然数を求めなさい。

(2)次の文章は、nが2以上あるときのn回目の作業で新たに書く自然数について、太郎さんが考えたことをまとめたものである。ア～エ にnを使った式を、それぞれ当てはまるように書きなさい。

n回目の作業で書く最も大きい自然数は［ ア ］である。
また、(n-1)回目の作業で書く最も大きい自然数は ［ イ ］であるから、n回目の作業では新たに［( ウ )］個の連続した自然数を書くことになる。
したがって、n回目の作業で、正方形の右下に書く自然数は、［ エ ］ である。

(3)10回目の作業について、
(ア)正方形の右下に書く自然数を求めなさい。
(イ)新たに書く自然数の和を求めなさい。

解答・解説

(1)
(ア) 9個
１回目・・・１個
２回目・・・３個
３回目・・・５個
４回目・・・７個
５回目・・・９個

(イ) 21
右下に書く自然数はn²-(n-1)で表せられる 5回目は 5²-(5-1)となる よって 21

(2)
ア n² , イ (n-1)² , ウ 2n-1 , エ n²-n+1
(ア) ｎ回目の作業後に自然数はｎ²個あるので、最も大きい自然数はｎ²
(イ) アと同様に（ｎ－１）回目の作業で書く最も大きい自然数は（ｎ－１）²
(ウ)
ｎ回目の作業で書く自然数は、ア、イより、
ｎ²－｛（ｎ－１）²｝＝ｎ²－（ｎ²－２ｎ＋１）＝２ｎ－１(個)
(エ)
ｎ回目の作業で右下に書く自然数は、新たに書かれた自然数のうちｎ番目。
つまり、（ｎ－１）²＋ｎ＝（ｎ²－２ｎ＋１）＋ｎ＝ｎ²－ｎ＋１

(3)
(ア) 91
10²-(10-1)=91
(イ) 1729
10回目に書く最も大きな数 10²=100
10回目に書く数の個数 2×10-1=19
10回目に書く最も小さい数は、9回目に書く最も大きい数の次の自然数なので9²+1=82
82～100までの19個の自然数の和は、182が19/2組なので 91×19 =1729

 岐阜県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！

教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！

受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。