和歌山県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。

また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 和歌山県の公立高校入試情報はこちら

大問1

問題文

〔問1〕 次の（1）～（5）を計算しなさい。
（1）2-6

（2）8/5+7/15×(-3)

（3）3(2a+b)-(a+5b)

（4）9/√3-√75

（5）a(a+2)+(a+1)(a-3)

〔問2〕 次の式を因数分解しなさい。
x²-12x+36

〔問3〕 絶対値が4以下の整数はいくつあるか，求めなさい。

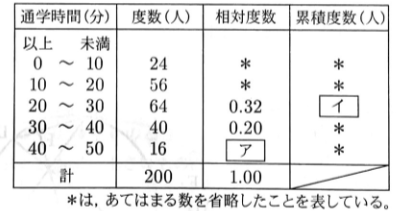
〔問4〕 次の表は，ある学年の生徒の通学時間を調査し，その結果を度数分布表にまとめたものである。 表中の【ア】，【イ】にあてはまる数をそれぞれ求めなさい。

〔問5〕 yはxの2乗に比例し，x=3のとき，y=-18である。
このとき，yをxの式で表しなさい。

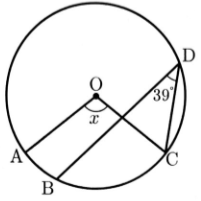
〔問6〕右の図のように，円Oの周上に4点A，B，C，Dがある。∠BDC=39°，BC= 3ABのとき，∠xの大きさを求めなさい。

解答・解説

問1
（1）-4
符号が違う計算は絶対値の差になる。符号は絶対値が大きい方のものになる。

（2）⅕
掛け算・割り算から先に計算する。

（3）5a-2b
（与式）=6a+3b-a-5b=5a-2b

（4）-2√3
ルートの有理化を行う。
（与式）=3√3-5√3=-2√3

（5）2a^2-3
展開をして、同類項をまとめる。
（与式）=a^2+2a+a^2-2a-3=2a^2-3

問２　(x-6)^2
掛けて「３６」、足して「－１２」になるペアを探せばよい

問３　９つ
整数０を忘れずに

問４　ア：0.08　イ：144
アは１６÷２００、イは24 + 56 + 64で求まる。

問５　y=-2x^2
y=ax^2の式に代入して求める。

問６　104°
弧BC=3弧ABより、弧AC=4弧AB
弧の比と円周角の比は等しくなるので、弧ACの円周角をｙとすると、
３：４＝３９：ｙ。これをを解くと、弧ACの円周角は52°だとわかる。
よって、ｘは中心角であり、ｙの２倍なので、104°が答えとなる。

大問2

問題文

次の〔問1〕～〔問5〕に答えなさい。
〔問1〕図1の展開図をもとにして，図2のように正四角錘Pをつくった。
次の（1），（2）に答えなさい。

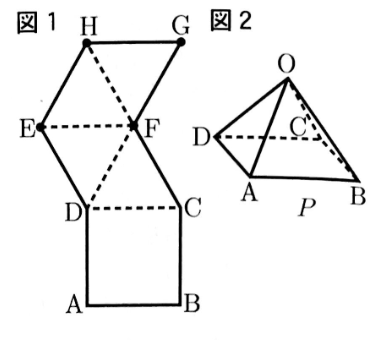
（1）図2において，点Aと重なる点を図1のE，F，G，Hの中から1つ選び，その記号をかきなさい。

（2）正四角錐Pの辺OA上にOI:IA=1:2となる点Iをとる。
図3のように，点Iを通り，底面ABCDに平行な平面で分けられた2つの立体をそれぞれQ，Rとする。
このとき，QとRの体積の比を求め，最も簡単な整数の比で表しなさい。

〔問2〕1辺の長さが7cmの正方形である緑，赤，青の3種類の色紙がある。
この色紙を，図のように左から緑，赤，青の順に繰り返して右に2cmずつずらして並べていく。
表は，この規則に従って並べたときの色紙の枚数，一番右の色紙の色横の長さについてまとめたものである。
このとき下の（1），（2）に答えなさい。

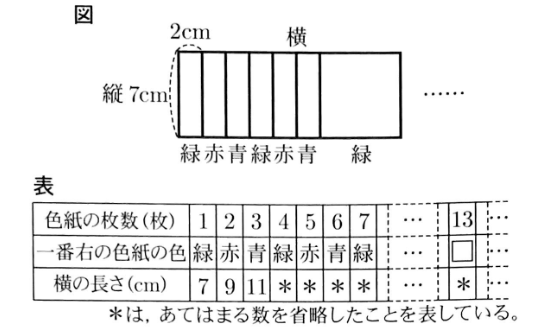
（1）表中の【 】にあてはまる色をかきなさい。

（2）色紙をn枚並べたときの横の長さをnの式で表しなさい。

〔問3〕2つのさいころを同時に投げるとき 出る目の数の積が12の約数になる確率を求めなさい。
ただし，さいころの 1 から 6までのどの目が出ることも同様に確からしいものとする。

〔問4〕 右の表は，ある洋菓子店でドーナツとカップケーキをそれぞれ1個つくるときの
小麦粉の分量を表したものである。
この分量にしたがって， 小麦粉400gを余らせることなく使用して，ド ーナツとカップケーキをあわせて18個つくった。
このとき，つくったド ーナツとカップケーキはそれぞれ何個か，求めなさい。
ただし， 答えを求める過程がわかるようにかきなさい。

〔問5〕 右の箱ひげ図は，太郎さんを含む 15 人のハンドボ ー ル投げの記録を表したものである。
また，次の文は太郎さんと先生の会話の一部である。

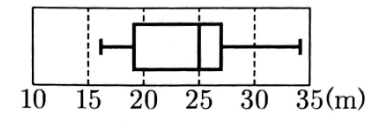
太郎：先生，15人のハンドボール投げの記録の平均値は何 m ですか。わたしの記録は 24.0 m でした。先生：平均値は 23.9mです。
太郎：そうすると，わたしの記録は平均値より大きいから， 15 人の記録の中で上位 8 番以内に入りますね。

下線部の太郎さんの言った内容は正しくありません。その理由をかきなさい。

解答・解説

問１
（１）E
展開図を組み立てるとわかる。

（２）１：２６
立体Pと立体Qは相似なので、体積比は相似比の三乗になり、3^3：1^3＝27:1となる。
よって、Qの体積：Rの体積＝1:(27-1)=1:26

問２
（１）緑
3で割ったときに余りが１なら緑、２なら赤、０なら青になる。
13÷3=4あまり1なので、緑色が正解。

（２）2n+5
１枚増えるごとに2cmずつ増えることに注目すればよいので、7+(n-1)×2となる。

問３　4/9
12の約数は「1,2,3,4,6,12」の６つ。出た目の数がこのいずれかになるのは16通りなので、16/36=4/9が答えとなる。

問４
連立方程式で解いていけばよい。
ドーナツをｘ個、カップケーキをｙ個作ったとすると
ｘ＋ｙ＝１８
２５ｘ＋１５ｙ＝４００
という２本の式が出来るので、これを解けばよい。
すると、ｘ＝１３、ｙ＝５となる。
よって、ドーナツ１３個、カップケーキ５個が答えとなる。

問５
【例】１５人の記録の中央値は２５ｍである。すると、太郎さんの記録は中央値より小さいので、上位８番に入ることはない。

大問3

問題文

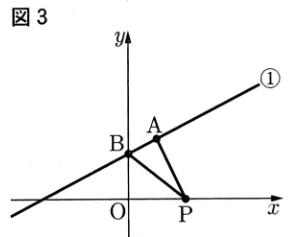
図1のように関数y=x+3・・・①のグラフ上に点A（2，4）があり，x軸上に点Pがある。
次の〔問1〕～〔問4〕に答えなさい。

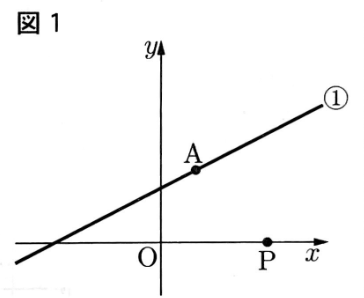
〔問1〕関数y=1/2x+3について，xの増加量が4のとき，yの増加量を求めなさい。

〔問2〕Pのx座標が6のとき直線APの式を求めなさい。

〔問3〕図2のように∠APO=30°のとき，Pのx座標を求めなさい。

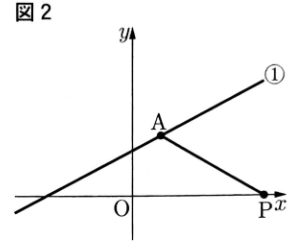
〔問4〕図3のように，①のグラフとy軸との 交点をBとする。
また，y軸上に点Qを とり，△ABPと△ABQの面積が等しくなるよう にする。
Pのx座標が4のとき，Qの座標をすべて求めなさい。

解答・解説

問１　２
傾きはｙの増加量/ｘの増加量なので、½=y/4よって、ｙの増加量は２

問２　y=-x+6
２点A（2,4）P（6,0）を通る直線の式を求めればよい。

問３　2+4√3
点Aから垂線をおろし、ｘ軸との交点をHとすると、点H（2,0）となる。
さらに三角形AHPは1:2:√3の有名な直角三角形になることがわかる。
AH:HP＝1:√3＝4:HP
これを解くと、HP=4√3となるので、点Pのｘ座標は2+4√3である。

問４　（0,-2）と（0,8）
①とｘ軸の交点を点R（-6,0）とすると
△ABPの面積は△APRから△BPRを引けば求まり、
10×4×1/2-10×3×1/2=5である。
△ABQはｙ軸上の点なので、面積は
△ABQ＝2×BQ×1/2=BQとなる。
つまり、BQの長さが5となる点Qの座標を取ればよい。

大問4

問題文

平行四辺形ABCDの辺BC上に点Eがある。
ただし，辺BCの長さは辺ABの長さより長いものとする。
次の〔問1〕～〔問4〕に答えなさい。

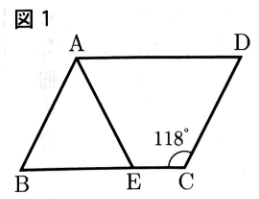
〔問1〕図1のようにAB= AE，∠BCD=118°のとき，∠BAEの大きさを求めなさい。

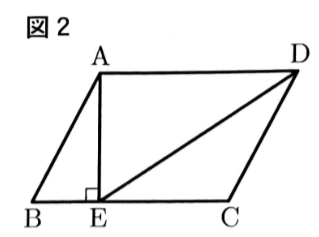
〔問2〕図2のように，BC=5cm，AE=3cm，∠AEB=90° のとき， 線分DEの長さを求めなさい。

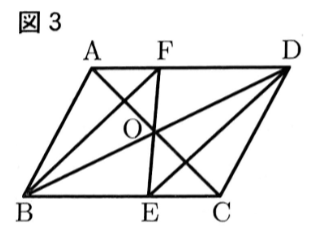
〔問 3 〕 図3のように，平行四辺形ABCDの対角線の交点をOとし，直線EOと辺ADの交点をFとする。
このとき，四角形BEDFは平行四辺形であることを証明しなさい。

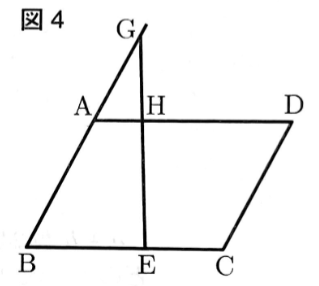
〔問4〕図4のように，AB=4cm，BE=3cm，EC=2cmのとき辺BAの延長上にAG=2cmとなるように点Gをとる。
また，GEとADの交点をHとする。
このとき台形ABEHの面積は，平行四辺形ABCDの面積の何倍になるか，求めなさい。

解答例

問１　56°
∠ABC＋∠BCD＝180°より、∠ABC＝62°
AB=AEより、△ABEは二等辺三角形、よって、∠BAE＝56°

問２　√34ｃｍ
平行四辺形の対辺の長さは等しいので、AD=BC=5ｃｍ
よって、直角三角形AEDにおいて、三平方の定理を使えば求まる。

問３　
△OBEと△ODFにおいて
Oは平行四辺形の対角線の交点なので
OB=OD・・・①
BE//FDより、錯覚が等しく
∠OBE＝∠ODF・・・②
対頂角は等しいので
∠BOE＝∠DOF・・・③
①～③より、１辺とその両端の角の大きさがそれぞれ等しいので、
△OBE≡△ODF
対応する辺の長さは等しいので
OE＝OF・・・④
①、④より、四角形BEDFの対角線はそれぞれの中点で交わるので、四角形BEDFは平行四辺形である。

問４　2/5倍
△GAH∽△GBEより、AH:BE=GA:GB、これを解くと、AH=1ｃｍ
平行四辺形ABCDで、底辺をBCとしたときの高さをhとすると、
平行四辺形ABCDの面積は5hと表せる。
また、台形ABEHの面積は2hと表せることから、
2/5倍だと導くことができる。

 和歌山県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、過去の入試問題も分析し和歌山県の入試問題の傾向やチェックポイントなどをまとめて、受験対策を行っています。

家庭教師のやる気アシストは高校受験に強い家庭教師！昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました！その 高い合格率の秘訣は、過去問を分析した対策や指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！

家庭教師のやる気アシストなら、お子さんの志望校に合わせた指導で合格まで全力でサポートさせて頂きます！
受験当日までの限られた時間です。少しでも気になった方は、すぐにお問合せ下さい！
1日でも早く対策を始めることが合格への近道です。

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。