大阪府の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

大阪府の数学問題は、レベル別にＡＢＣの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Ａが易、Ｂがやや難、Ｃが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。

 大阪府の公立高校入試情報はこちら

【数学A】大問1

問題文

次の計算をしなさい。

(1) 5×(－4)+7

(2) 3.4－(－2.5)

(3) 2×4²

(4) 8x－3+2(x+1)

(5) －18xy÷3x

(6) √5+√45

解答・解説

(1) －13
－20+7=－13

(2) 5.9
3.4+2.5＝5.9

(3) 32
2×16＝32

(4) 10x－1
8x－3+2x+2＝10x－1

(5) －6y

(6) 4√5
√5+3√5＝4√5

大問2

問題文

次の問いに答えなさい。

(1) -7/4は、右の数直線上のア〜エで示されている範囲のうち、どの範囲に入っていますか。一つ選び、記号を〇で囲みなさい。

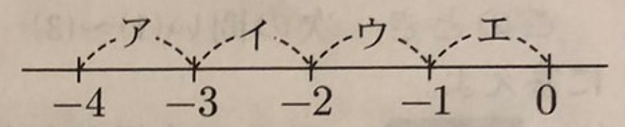
(2) a=－3のとき、4a+21の値を求めなさい。

(3) nを整数とするとき、次の ア〜エの式のうち、その値がつねに3の倍数となるものはどれですか。一つ選び、記号を〇で囲みなさい。

(4) ［1個の重さが a g のビー玉2個と、1個の重さが b g のビー玉7個の重さの合計］をa、bを用いて表しなさい。

(5) 正五角形の内角の和を求めなさい。

(6) 下図は、ある中学校の卓球部の部員が行った反復横とびの記録を箱ひげ図に表したものである。卓球部の部員が行った反復横とびの記録の四分位範囲を求めなさい。

(7) 連立方程式x－3y=10、5x+3y=14を解きなさい。

(8) 二次方程式x²－2x-35=0を解きなさい。

(9) 二つのさいころを同時に投げるとき、出る目の数の和が10より大きい確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。

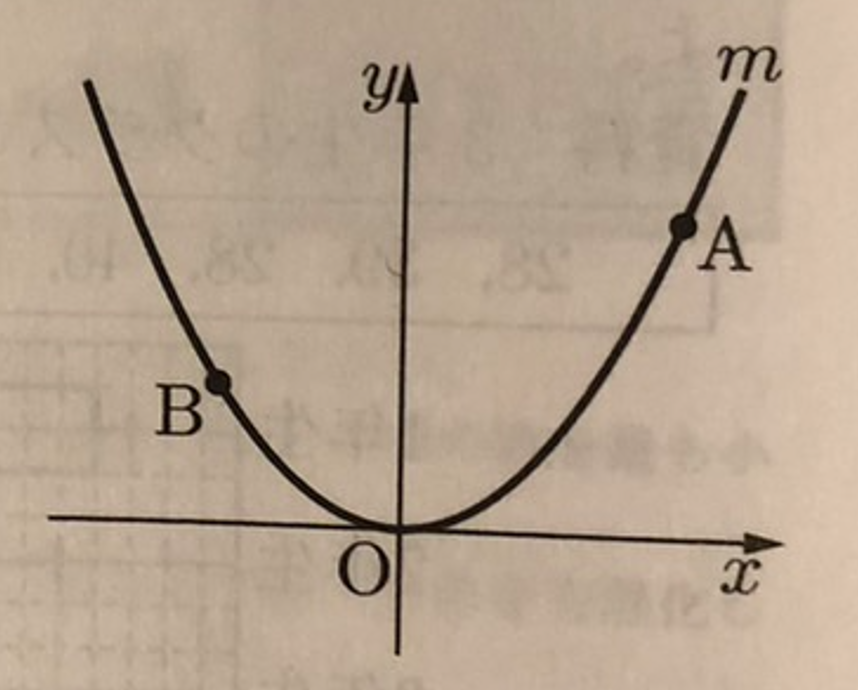
(10) 下図において、mは関数y=ax²(aは正の定数)のグラフを表す。A、Bはm上の点であって、Aのx座標は3であり、Bのx座標は－2である。Aのy座標はBのy座標より2大きい。aの値を求めなさい。

(11) 下図において、立体ABCD-EFGHは直方体である。次のア〜エのうち、辺ABと垂直な面はどれですか。一つ選び、記号を〇で囲みなさい。

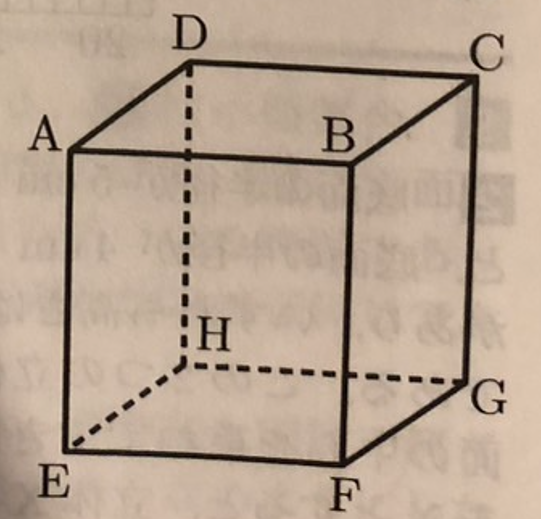
ア 面ABCD
イ 面BFGC
ウ 面AEFB
エ 面EFGH

解答・解説

(1) ウ
-7/4=－1.75なので、ウが適切。

(2) 9
4a+21=4×(－3)+21=－12+21=9・・・(A)

(3) エ
3n+6=3(n+2)となる。nは整数であるからn+2も整数となり、3(n+2)は3の倍数である。
よって、エが適切。

(4) 2a+7b(g)

(5) 540°
180°×(5-2)=540°・・・(A)

(6) 5回

(7) x=4, y=-2
x－3y=10
+) 5x+3y=14
6x =24
x =4

x=4をx－3y=10に代入して、
4－3y=10
3y=－6
y=－2

(8) x=－5、7
x²－2x-35=0
(x+5)(x-7)=0
x=－5、7

(9) 1/12
出る目の数の和が10より大きくなる組み合わせは、(5，6)、(6，5)、(6，6)の3通りなので、
3/36=1/12・・・(A)

(10) a=2/5
A、Bそれぞれの座標は、A(3，9a)、B(－2、4a)となる。
Aのy座標はBのy座標より2大きいので、9a=4a+2 したがって、a=2/5・・・(A)

(11) イ

大問3

問題文

自宅で加湿器を利用しているDさんは、加湿器を使うと加湿器のタンクの水の量が一定の割合で減っていくことに興味をもち、「加湿器を使用した時間」と「タンクの水の量」との関係について考えることにした。
初めの「タンクの水の量」は840mLである。加湿器を利用したとき、「タンクの水の量」は毎分6mLの割合で減る。
次の問いに答えなさい。

(1) 「加湿器を使用した時間」がx分のときの「タンクの水の量」をymLとする。また、0≦x≦140とし、x=0のとき、y=840であるとする。
➀次の表は、xとyとの関係を示した表の一部である。表中の(ア)、(イ)に当てはまる数をそれぞれ書きなさい。

②yをxの式で表しなさい。

(2) Dさんは、タンクに水が840mL入った状態から加湿器を使い始め、しばらくしてタンクの水の量が450mLまで減っていることに気が付いた。Dさんは、加湿器を使用した時間について考えてみた。
「加湿器を使用した時間」をt分とする。「タンクの水の量」が450mLであるときのtの値を求めなさい。

解答・解説

(1) ➀
(ア) 822
(イ) 786

② y=－6x+840

(2) t=6
y=－6x+840にx=t、y=450を代入して、
450=－6t+840
6t=390
t=65

大問4

問題文

下図において、四角形ABCDは内角ABCが鋭角の平行四辺形であり、AB=4㎝、AD=8㎝である。Eは、Dから直線ABにひいた垂線と直線ABとの交点である。このとき、ED⊥DCである。EとCとを結ぶ。Fは、線分ECと辺ADとの交点である。Gは、Dから直線BCにひいた垂線と直線BCとの交点である。DC=x㎝とし、0<x<4とする。
次の問いに答えなさい。

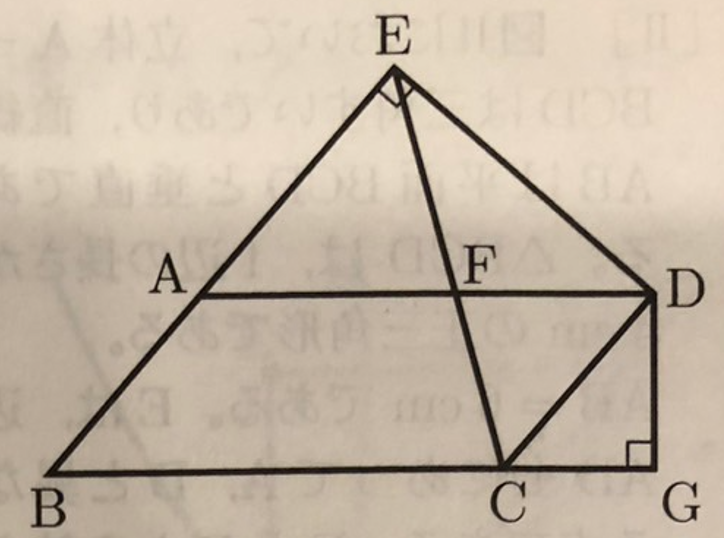
(1) 次のア〜エのうち、△DCGを直線DCを軸として1回転させてできる立体の名称として正しいものはどれですか。一つ選び、記号を〇で囲みなさい。
ア 三角柱
イ 円柱
ウ 三角すい
エ 円すい

(2) 四角形ABCDの面積をxを用いて表しなさい。

(3) 次は、△FAD∽△GCDであることの証明である。【 a 】、【 b 】に入れるのに適している「角を表す文字」をそれぞれ書きなさい。また、c[ ]に適しているものを一つ選び、記号を〇で囲みなさい。

(証明)
△FADと△GCDにおいて
DE⊥EB、DG⊥BGだから
∠DEA=∠【 a 】=90°・・・あ
EB//DCであり、平行線の錯角は等しいから
∠EAD=∠ADC・・・い
AD//BGであり、平行線の錯角は等しいから
∠【 b 】=∠ADC・・・う
い、う より ∠EAD=∠【 b 】・・・え
あ、え より、
ｃ[
ア 1組の辺とその両端の角
イ 2組の辺の比とその間の角
ウ 2組の角
]
がそれぞれ等しいから、
△EAD∽△GCD

(4) x=3であるときの線分ECの長さを求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。

解答・解説

(1) エ

(2) 8x(㎠)

(3)
【 a 】→DGC
【 b 】→GCD
c→ウ

(4) 2√13(㎝)
△EAD∽△GCDより、
ED：GD=DA：DC=8：4=2：1
よって、
ED=2DG=2×3=6(㎝)
∠EDC=90°より、三平方の定理から
EC=√(6²+4²)=√(36+16)=√52=2√13(㎝)・・・(A)

【数学B】大問1

問題文

(1) 2×(－3)－4²

(2) 5(2a+b)－4(a+3b)

(3) 2a×9ab÷6a²

(4) (x+1)²+x(x－2)

(5) (2√5+√3)(2√5-√3)

解答・解説

(1)－22
－6－16＝－22

(2) 6a－7b
10a+5b－4a－12b＝6a－7b

(3) 3b

(4) 2x²+1
x²+2x+1+x²－2x＝2x²+1

(5) 17
(2√5)²-√3²＝20－3＝17

大問2

問題文

(1) a＝－6、b＝5のとき、a²－8bの値を求めなさい。

(2) 二次方程式x²－11x+18＝0を解きなさい。

(3) nを自然数とするとき、5－78nの値が自然数となるような最も小さいnの値を求めなさい。

(4) 関数y=10/xについて、xの値が1から5まで増加するときの変化の割合を求めなさい。

(5) 二つの箱A、Bがある。箱Aには自然数の書いてある3枚のカード[1]、[2]、[3]が入っており、箱Bには奇数の書いてある5枚のカード[1]、[3]、[5]、[7]、[9]が入っている。A、Bそれぞれの箱から同時にカードを1枚ずつ取り出し、箱Aから取り出したカードに書いてある数をa、箱Bから取り出したカードに書いてある数をbとする。このとき、baの値が1より大きく4より小さい数になる確率はいくらですか。A、Bそれぞれの箱において、どのカードが取り出されることも同様に確からしいものとして答えなさい。

(6) ある中学校の剣道部、卓球部、水泳部の部員が反復横とびの測定を行った。下図は、その記録を箱ひげ図に表したものである。次のア〜オのうち、右図からわかることとして正しいものはどれですか。すべて選び、記号を〇で囲みなさい。

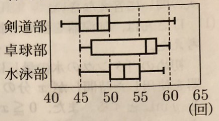
ア. 三つの部の部員のうち、記録が60回以上の部員は1人だけである。
イ. 剣道部の記録の四分位範囲と、水泳部の記録の四分位範囲は同じである。
ウ. 三つの部のうち、記録の範囲が最も大きいのは卓球部である。
エ. 第一四分位数が最も小さいのは、水泳部の記録である。
オ. 卓球部では、半数以上の部員の記録が55回以上である。

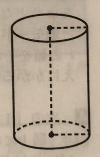
(7) 下図の立体は、底面の半径が4㎝、高さがa㎝の円柱である。下図の円柱の表面積は120π㎠である。aの値を求めなさい。

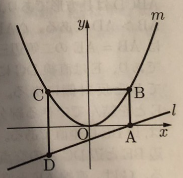
(8) 下図において、mは関数y＝ax²(aは正の定数)のグラフを表し、lは関数y＝13x－1のグラフを表す。Aはlとx軸との交点である。Bは、Aを通りy軸に平行な直線とmとの交点である。Cは、Bを通りx軸に平行な直線とmとの交点のうちBと異なる点である。Dは、Cを通りy軸に平行な直線とlとの交点である。四角形ABCDの面積は21㎠である。aの値を求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。ただし、原点Oから点(1，0)までの距離、原点Oから点(0，1)までの距離はそれぞれ1㎝であるとする。

解答・解説

(1) －4
a²－8b＝(－6)²－8×5＝36－40＝－4

(2) x＝2、9
x²－11x+18＝0
(x－2)(x－9)＝0
x＝2、9

(3) 26
5－78/nは自然数のため、5>78/n
よって、 n>78/5=15.6
nが16以上で78/nが自然数となる最小のnは、78/26＝3より26
したがって、求める最も小さいnの値は26・・・(A)

(4) －2
x＝1のとき、 y＝10
x＝5のとき、 y＝2
よって、求める変化の割合は 2－105－1＝-84＝－2・・・(A)

(5) 7/15
b/aの値は全部で 3×5＝15通りある。
この内1<b/a<4となるのは、
(a，b)＝(1，3)、(2，3)、(2，5)、(2，7)、(3，5)、(3，7)、(3，9)
の4通りである。よって、求める確率は7/15・・・(A)

(6) イ、オ

(7) a＝11
底面積は 4×4×π＝16π
側面積は a×(2×4×π)＝8πa
と表せる。よって表面積について、
16π×2+8πa＝120π
32π+8πa＝120π
4+a＝15
a＝11・・・(A)

(8) a＝5/18
A、B、C、Dそれぞれの座標を求める。
Aのx座標はlにy＝0を代入して、 x＝3 ∴A(3，0)
Bのx座標はAと同じで3。これをmに代入して、 y＝9a ∴B(3，9a)
Cはy軸に関してBと対称な点であるから、 C(－3，9a)
Dのx座標はCと同じで－3。これをlに代入して、 y＝－2 ∴D(－3，－2)
よって、AB＝9a㎝、CD＝9a+2㎝、BC＝6㎝と表せる。
したがって、四角形ABCDの面積について
(9a+9a+2)×6×12＝21
18a+2＝7
18a＝5
a＝518・・・(A)

大問3

問題文

自宅で加湿器を利用しているDさんは、加湿器を使うと加湿器のタンクの水の量が一定の割合で減っていくことに興味をもち、「加湿器を使用した時間」と「タンクの水の量」との関係について考えることにした。Dさんの自宅の加湿器は、強モード、弱モードのどちらかのモードを選んで使うことができる。タンクには水が840mL入っており、強モードで使用する場合「タンクの水の量」は毎分6mLの割合で減り、弱モードで仕様する場合「タンクの水の量」は毎分2mLの割合で減る。
次の問いに答えなさい。

(1) Dさんは加湿器を強モードで使用する場合について考えた。
初めの「タンクの水の量」は840mLである。「加湿器を使用した時間」がx分のときの「タンクの水の量」をymLとする。また、0≦x≦140とし、x=0のとき、y=840であるとする。

①次の表は、xとyの関係を示した表の一部である。表中の(ア)、(イ)に当てはまる数をそれぞれ書きなさい。

②yをxの式で表しなさい。

③y＝450となるときのxの値を求めなさい。

(2) Dさんは、タンクに水が840mL入った状態から加湿器を使い始め、途中でモードを切りかえて使用した。
初めの「タンクの水の量」は840mLである。加湿器を最初は強モードでs分使用し、その後続けて弱モードに切りかえてt分使用したところ、タンクの水はちょうどなくなった。加湿器を強モードで使用した時間と弱モードで使用した時間の合計は192分であった。s、tの値をそれぞれ求めなさい。ただし、モードの切りかえにかかる時間はないものとする。

解答・解説

(1) ➀
(ア) 822
(イ) 786

② y=－6x+840

③ x＝65
450＝－6x+840
6x＝390
x＝65・・・(A)

(2) s＝114、t＝78
sとtについて次の連立方程式が成り立つ。
加湿器を使用した合計時間について、 s+t＝192・・・①
減ったタンクの水の量について、 6s+2t＝840・・・②
②－①×2をして、 4s＝456 ∴s＝114
これを①に代入して、 114+t＝192 ∴t＝78
したがって、 s＝114、t＝78・・・(A)

大問4

問題文

次の［Ⅰ］、［Ⅱ］に答えなさい。

［Ⅰ］図Ⅰにおいて、四角形ABCDは長方形であり、AB>ADである。△ABEはAB=AEの二等辺三角形であり、Eは直線DCについてBと反対側にある。DとEとを結んでできる線分DEは、辺BEに垂直である。Fは、辺BEと辺DCとの交点である。Gは、直線AEと直線BCとの交点である。次の問いに答えなさい。

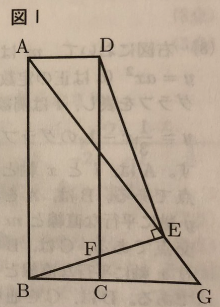
(1) △AED∽△GBEであることを証明しなさい。

(2) AB＝4㎝、BG＝3㎝であるとき、
①辺ADの長さを求めなさい。
②線分FCの長さを求めなさい。

［Ⅱ］図Ⅱにおいて、立体A－BCDは三角すいであり、直線ABは平面BCDと垂直である。三角BCDは、1辺の長さが4㎝の正三角形である。
AB＝6㎝である。Eは辺AD上にあってＡ、Ｄと異なる点である。EとBとを結ぶ。Fは、Eを通り辺DBに平行な直線と辺ABとの交点である。Gは、Eを通り辺ABに平行な直線と辺DBとの交点である。Hは、Eを通り辺ACに平行な直線と辺CDとの交点である。HとBとを結ぶ。
次の問いに答えなさい。

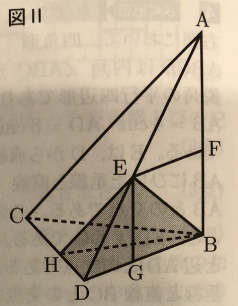
(3) 次のア〜エのうち、線分EHとねじれの位置にある辺はどれですか。一つ選び、記号を〇で囲みなさい。
ア 辺AB
イ 辺AC
ウ 辺AD
エ 辺CD

(4) EF＝EGであるとき、
①線分EGの長さを求めなさい。
②立体EHDBの体積を求めなさい。

解答・解説

［Ⅰ］
(1)
AD//BGなので、平行線の錯角より ∠EAD=∠BGE・・・①
∠AED＝90°－∠AEB・・・②
∠GBE＝90°－∠ABE・・・③
△ABEは二等辺三角形より、 ∠ABE＝∠AEB・・・④
②③④より、 ∠AED＝∠GBE・・・⑤
①⑤より、2組の角がそれぞれ等しいので、△AED∽△GBE

(2)
① 4/3(㎝)
△ABGについて、三平方の定理より、 AG＝√(4²+3²)＝√25＝5㎝
AB＝AEより、 AE＝4㎝
よって、 GE＝AB－AE＝5－4＝1㎝
△AEDと△GBEについて、相似比はAE：GB＝4：3
よって、AD＝GE×43＝1×43＝43(㎝)・・・(A)

② 4/9(㎝)
CG＝3－43＝53(㎝)
辺AGと辺DCの交点をHとすると、AB//DCより、 △ABG∽△HCG
BG：AB：AG＝3：4：5より、CG：HC：HG＝3：4：5だがら、
HC＝53×43＝209(㎝)
HG＝53×53＝259(㎝)
AB//DCより、△ABE∽△HFEだから、
HF＝HE＝HG－GE＝259－1＝169(㎝)
よって、 FC＝HC－HF＝209－169＝49(㎝)・・・(A)

［Ⅱ］
(3) ア

(4) ①12/5(㎝)
四角形EGBFは正方形だから、EG＝x㎝とおくと、
△ADB∽△AEFより、
x：6＝(4－x)：4
4x＝24－6x
10x＝24
x＝125
よって、EG＝125(㎝)・・・(A)

② 32√3/25(㎤)
AC//EH、EF//DBより、
CH：HD＝AE：ED＝AF：FB
＝(6－125)：125＝185：125＝3：2
△BCD＝12×4×2√3＝4√3だから、
△BHD＝4√3×23+2＝8√35
よって、求める体積は、△BHDを底面とする高さがEGの三角すいの体積だから、
13×8√35×125＝32√325(㎤)・・・(A)

【数学C】大問1

問題文

(1) -a× (2ab)²÷(-2ab²)/3　を計算しなさい。

(2) (6+√8 )/√2 + (2-√2)² を計算しなさい。

(3) aを0でない定数とする。ax²+4x-7a-16=0 の二次方程式の一つの解が x=3 であるとき、aの値を求めなさい。また、この方程式のもう一つの解を求めなさい。

(4) a,b,c,d を定数とし、a>0, b<0, cくdとする。関数 y＝ax² と関数y=bx+1 について、xの変域が　-3≦x≤1 のときの yの変域がともに c≦y≦d であるとき，a,b の値をそれぞれ求めなさい。

(5) nを自然数とする。n≦√x≦n+1 を満たす自然数 x の個数が100であるときの n の値を求めなさい。

(6) 二つの箱A、B がある。 箱Aには 1 から 4 までの自然数が書いてある4枚のカード 1⃣2⃣3⃣4⃣　が入っており、箱Bには 4 から 8 までの自然数が書いてある5枚のカード4⃣5⃣6⃣7⃣8⃣　が入っている。 A、B それぞれの箱から同時にカードを1枚ずつ取り出し、箱Aから取り出したカードに書いてある数をa、 箱Bから取り出したカードに書いてある数をbとして、次のきまりにしたがって得点を決めるとき、 得点が偶数である確率はいくらですか。 A、B それぞれの箱において、どのカードが取り出されることも同様に確からしいものとして答えなさい。

(7) aを一の位の数が0でない2けたの自然数とし、bをaの十の位の数と一の位の数とを入れかえてできる自然数とするとき、(b²-a²)/99 の値が24であるaの値をすべて求めなさい。

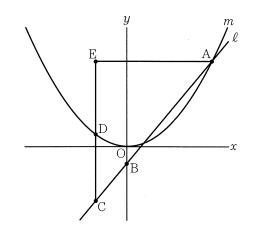
(8) 下図において, m は関数 y=x²/5 のグラフを表す。 Aはm上の点であり、そのx座標は5である。Bは y軸上の点であり、そのy座標は-1である。l は、2点A, B を通る直線である。 Cはl 上の点であり、 そのx座標は負である。 Cのx座標をtとし,t<0 とする。 D はCを通りy軸に平行な直線とmとの交点である。 E は、 A を通りx軸に平行な直線と 直線 DC との交点である。 線分 DC の長さが線分 EA の長さより3cm短いときの t の値を求めなさい。答えを求める過程がわかるように、 途中の式を含めた求め方も説明すること。 ただし、 原点から点 (1,0)までの距離、 原点Oから点 (0,1)までの距離はそれぞれ1cmであるとする。

解答・解説

(1) 6a²
-a× (2ab)²×-3/(2ab²)=6a²

(2) 8-√2
(6+√8)/√2+(2-√2)²=(6+√8)/√2×√2/√2+4-4√2+2=(6√2+4)/2+6-4√2=3√2+2+6-4√2=8-√2

(3) aの値：2　もう一つの解：x=-5
x=3を与式に代入すると、9a+12-7a-16=0
整理すると、2a-4=0 よってa=2
a=2を与式に代入すると、2x²+4x-7×2-16=0
整理すると、2x²+4x-30=0
⇒（x-3）×（2x+10）=0 よってもう一つの解は、x=-5

(4) aの値：4/9　bの値：-1

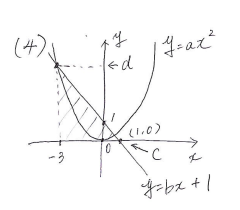
上図より、c=0である。よって、(1，0)をy=bx+1に代入して、
0=b+1
b=－1
これは、b<0に適する。
また、(－3，d)をy=－x+1に代入して、
d=3+1 d=4
これは、c<dに適する。
(－3，4)をy=ax²に代入すると、
4=9a a=49
これは、a>0に適する。
したがって、 a=49、b=－1・・・(A)

(5) n=49
全返を2乗すると、 n²≦x≦(n+1)²
よって、 (n+1)²－n²+1=2n+2が100となるときのnを求めればよい。
2n+2=100を解くと、 n=49・・・(A)

(6) 7/20
きまり：a と b の最大公約数が1の場合は α+b の値を得点とし、αとb の最大公約数が1以外の場合は√(2ab)の値を得点とする。
取り出し方は全部で 4×5=20通り。
このうち得点が偶数になるのは
(a，b)=(1，5)、(1，7)、(2，4)、(3，5)、(3，6)、(3，7)、(4，8)
の7通りあるから、求める確率は7/20・・・(A)

(7) a=15、57
aの一の位をx、十の位をyとおくと(0≦x≦9、0<y≦9)、
a=10y+x、b=10x+yと表せる。
b²-a²/99=(10x+y)²-(10y+x)²/99=(100x²+20xy+y²)-(100y²+20xy+x²)/99=99(x²-y²)/99=x²－y²
したがって、 x²－y²=24
これを満たすx、yは、 (x，y)=(5，1)、(7，5)
これは0≦x≦9、0<y≦9を満たす。
よって求めるaの値は a=15、57・・・(A)

(8) t=1－√21/2
Aのx座標は5であるから、これをy=1/5x²に代入して、y=5 よって、A(5，5)
また直線lはA(5，5)とB(0，－1)の2点を通る直線であるからその式は y=6/5x－1と求められる。
Cのx座標はtでこれは直線y=65x－1を通るから、 C(t，6/5t－1)
Dのx座標はtでこれはy=15x²上の点であるから、 D(t，1/5t²)
条件より、E(t，5)
よって
DC=1/5t²－(6/5t－1)=1/5t²－6/5t+1
EA=5－t
と表せる。したがってDC=EA－3より、
1/5t²－6/5t+1=5－t－3
t²－6t+5=10－5t
t²－t－5=0
2次方程式の解の公式より、 t=1±√21/2
t<0だから、 t=1－√21/2・・・(A)

大問2

問題文

図 I, 図II において、 四角形ABCD は内角∠ABC が鋭角のひし形であり、AB=7cmである。 △DCE は鋭角三角形であり、Eは直線 BC 上にある。 Fは辺 DE 上にあって D, E と異なる点であり、BとFとを結んでできる線分 BF は辺 DE に垂直である。 G は、 Cから辺AB にひいた垂線と辺AB との交点である。H は辺 CE 上の点であり、 CH = GB である。 DとHとを結ぶ。
次の問いに答えなさい。

(1)　図Ⅰにおいて

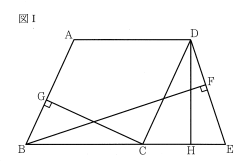
① 四角形ABCD の対角線 AC の長さを a cm、四角形ABCDの面積をScmとするとき, 四角形 ABCD の対角線 BD の長さをα, Sを用いて表しなさい。

②△DHE∽△BFE であることを証明しなさい。

⑵　図ⅡにおいてGB = 2cm、HE =3cm である。 I は、 線分 BFと辺 DC との交点である。 J は、直線 BF と直線ADとの交点である。

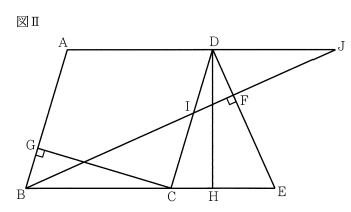
①　線分FEの長さを求めなさい。

②　線分IJの長さを求めなさい。

解答・解説

(1)① BD=2S/a
AC×BD×1/2=Sであるから、 a×BD×1/2=S
整理して、 BD=2Sa・・・(A)

②
△DCHと△GBDにおいて、
四角形ABCDはひし形より、 DC=GB
仮定より、 CH=BG
平行線の同位角より、 ∠DCH=∠CBG
2組の辺とその間の角がそれぞれ等しいから、
△DCH≡△CBG
したがって、∠DHC=∠CGB=90°
△DHEと△BFEにおいて、
∠DHE=∠BFE=90°・・・➀
共通角より、 ∠DEH=∠BEF・・・②
➀②より、2組の角がそれぞれ等しいから、
△DHE∽△BFE

(2)① 2√6(㎝)
BE=7+2+3=12
DH=√(7²－2²)=√45=3√5
DE=√((3√5)²+3²)=√(45+9)=√54=3√6
△DHE∽△BFEより、 3：FE=3√6：12
整理すると、 FE=363√6=2√6(㎝)・・・(A)

② 18√30/13(㎝)
DJ//BEより、△DFJ∽△EFB
相似比は、 DF：EF=(3√6－2√6)：2√6=√6：2√6=1：2
BF=√(12²－(2√6)²)=√120=2√30
よって、
JF=2√30×1/2=√30
DJ= 12×1/2=6
BJ=2√30+√30=3√30
また、△DIJと△CIBについてその相似比は、 DJ：CB=6：7
したがって、 IJ=3√30×66+7=18√3013(㎝)・・・(A)

大問3

問題文

図Ⅰ、 図Ⅱにおいて、立体ABCD – EFGHは六つの平面で囲まれてできた立体である。四角形ABCDは、1辺の長さが2cm の正方形である。四角形EFGHは、EF = 6cm、FG = 4cm の長方形である。平面ABCDと平面EFGHは平行である。四角形AEFBは AB // EF の台形であり、AE = BF =4cm である。
四角形 DHGC ≡ 四角形 AEFB である。四角形BFGCはBC // FG の台形である。四角形 AEHD ≡ 四角形BFGCである。

次の問いに答えなさい。

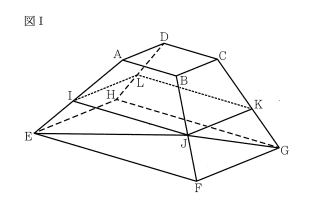
(1)　図1において, 四角形IJKLは長方形であり、I,J,K,Lはそれぞれ辺AE,BF,CG,DH上にある。このとき、AI=BJ=CK=DLである。EとJ、GとJとをそれぞれ結ぶ。
①　次のア～オのうち、辺BFとねじれの位置にある辺はどれですか。すべて選び、記号を〇で囲みなさい。
ア　辺AB
イ　辺EH
ウ　辺CG
エ　辺GH
オ　辺DH

②△JFGの面積は△JEFの面積の何倍ですか。

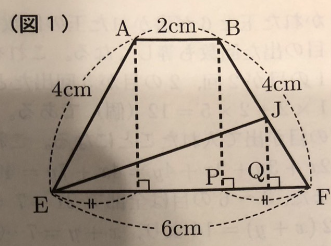
③ 四角形IJKLの周の長さが15cmであるときの辺JKの長さを求めなさい。

⑵　図Ⅱにおいて、MはBから平面EFGHにひいた垂線と平面EFGHとの交点である。N,Oは、それぞれ辺EF、HGの中点である。このとき、4点B,N,O,Cは同じ平面上にあり、この4点を結んでできる四角形BNOCはBC// NOの台形である。

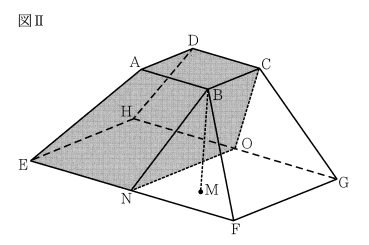
①　線分BMの長さを求めなさい。

②立体ABCD-ENOHの体積を求めなさい。

解答・解説

(1) ① イ、エ、オ
辺ABは点Bで交わる。また辺CGは同じ平面BFGC上にあり、平行でないので交わる。

② √5/3倍
点B、点Jからそれぞれ辺EFに垂線BP、JQを引く。
四角形AEFBは等脚台形だから、
PF=(6－2)÷2=2(㎝)
よって、
BP=√(4²－2²)=√12=2√3(㎝)
四角形BFGCについても同様に図2のようにして、
FR=(4－2)÷2=1(㎝)
BR=√(4²－1²)＝√15(㎝)
ここで、JQ：BP(=JF：BF)=JS：BRより、
JQ：JS=BP：BR=2√3：√15=2：√5
よって、
△JEF：△JFG=(1/2×6×2)：(1/2×4×√5)=6：2√5=3：√5
3△JFG=√5△JEFより、 △JFG=√5/3△JEF
したがって、√5/3倍・・・(A)

③ 19/6(㎝)
JF=x(㎝)とすると、FQ=x/2、FS=x/4より、
IJ=6－x/2×2=6－x(㎝)
JK=4－x/4×2=4－x/2(㎝)
だから、 2(6－x)+2(4－x/2)=15
これを解くと、 x=5/3
よって、 JK=4－5/3×1/2=19/6(㎝)・・・(A)

(2) ① √11(㎝)
点Cから辺HGに垂線CTを引くと、図3より、
PM=(4－2)÷2=1
BM=√((2√3)²－1²)=√11(㎝)・・・(A)

② 23√11/3(㎤)
立体ABCD－ENOHを、平面ANODで2つの立体AD－ENOHと立体ABCD－NOに切り分け、さらにこの2つの立体を、辺ABを含み面EFGHに垂直な平面と、辺DCを含み面EFGHに垂直な平面で切る。
立体AD－ENOHは、底面積と高さが等しい2つの四角すいと1つの三角柱に分けられるから、体積は、
1/3×(3×1)×√11×2+(1/2×3×√11)×2=2√11+3√11=5√11(㎤)
立体ABCD－NOは、底面積と高さが等しい2つの三角すいと1つの三角柱に分けられるから、体積は、
1/3×(1/2×2×√11)×1×2+(1/2×2×√11)×2=2√113+2√11=8√11/3(㎤)
したがって、求める体積は 5√11+8√11/3=23√11/3(㎤)・・・(A)

 大阪府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。