【兵庫県】令和4年度/2022年度入学者高校入試選抜試験：数学の解説
兵庫県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の兵庫県の数学は6つの大問で構成され、小問集合・連立方程式・図形・関数・確率・法則性を問う問題の構成になっています。後に行けば行くほど難しくなるお手本のような形式です。
難易度自体は例年よりも簡単でやや難でした。大問2までは完全解答を目指しましょう。逆に大問6はかなりの難問になっているので数学に自信がある方は一度挑戦してみてください。
【兵庫県】令和4年度一般入学者選抜の過去問はこちらから
大問1
問題文
次の問いに答えなさい。
(１) ３＋(ー７) を計算しなさい。
(２) ２(２x＋y)ー(xー５y) を計算しなさい。
(３) ２√３+ √２７ を計算しなさい。
(４) ９x²ー１２x＋４ を因数分解しなさい。
(５) 2次方程式 x²ーxー４＝０ を解きなさい。
(６) yはxに反比例し，x＝ー９のときy＝２である。x＝３のときのyの値を求めなさい。
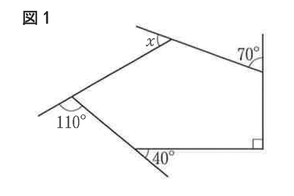
(７) 図１で，∠xの大きさは何度か、求めなさい。
(８) あるクラスの生徒が３５人が，数学と英語のテストを受けた。図２は，それぞれのテストについて，３５人の得点の分布のようすを箱ひげ図に表したものである。この図から読み取れることとして正しいものを，あとのア～エから全て選んで，その符号を書きなさい。
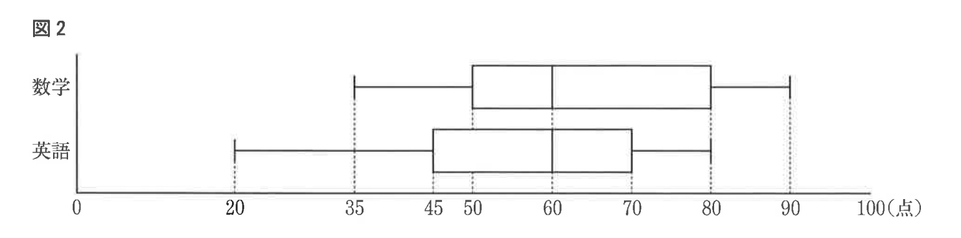
ア 数学，英語どちらの教科も平均点は６０点である。
イ 四分位範囲は，英語より数学の方が大きい。
ウ 数学と英語の合計得点が１７０点である生徒が必ずいる。
エ 数学の得点が８０点である生徒が必ずいる。
解答・解説
(１) 【正答 ー４】
(２) 【正答 ３x＋７y】
展開して計算すればよい
【与式】＝４x＋２yーx＋５y＝３x＋７y
(３) 【正答 ５√３】
√は二乗で外に出せる
【与式】＝２√３＋３√３＝５√３
(４) 【正答 (３xー２)²】
(x²ー２xy＋y²)＝(xーy)²の公式を使えばいい
【与式】＝(３x)²ー２(３x×２)＋２²＝(３xー２)²
(５) 【正答 (１±√１７）/２】
2次方程式(ax²＋bx＋ｃ＝０)の解の公式 x＝{ーb±√(b²ー4ac)}÷２a より
x＝{ ー(ー１)±√((ー１)²ー4×１×(ー１)) }÷(２×１)＝(１±√１７）/２
(６) 【正答 ー６】
反比例の式 ｙ＝a／x に x＝ー９，y＝２を代入する
２＝a／xー９ ⇔ a＝ー１８
よって、この反比例の式は
ｙ＝ー１８／x となる。
さらにこの式に x＝３を代入し、
ｙ＝ー１８／３＝ー６
(７) 【正答 ５０度】
外角の和は、角の数によらず360°になるので
360°＝x＋70°＋90°＋40°＋110°
⇔ x＝50°
(８) 【正答 イ，エ】
ア 数学，英語の中央値がともに60点である。平均値はこの箱ひげ図からは分からない。よって，アは誤り。
イ 数学の四分位範囲は，80ー50＝30
英語の四分位範囲は，70ー45＝25
英語より数学の方が大きくなっているので，イは正しい。
ウ 数学の最高点が90点，英語の最高点が80点であるが，同一人物がそれぞれの最高点を取ったかどうかは，箱ひげ図から分からない。よって，ウは誤り。
エ クラスの生徒が35人いるため，第３四分位数は一つの値から決まる。よって，数学の得点が80点である生徒が必ずいると言える。エは正しい。
大問2
問題文
P地点とQ地点があり，この２地点は980ｍ離れている。Ａさんは9時にちょうどいＰ地点を出発してＱ地点まで，Ｂさんは9時6分にＱ地点を出発してＰ地点まで，同じ道を歩いて移動した。図は，ＡさんとＢさんのそれぞれについて，9時ｘ分におけるＰ地点からの距離をｙｍとして，ｘとｙの関係を表したグラフである。
次の問いに答えなさい。
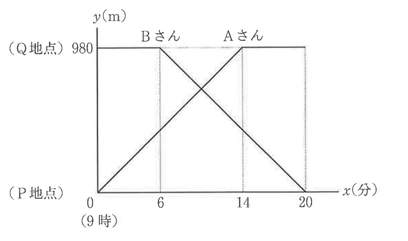
(１) 9時ちょうどから9時14分まで，Aさんは分速何ｍで歩いたか，求めなさい。
(２) 9時6分から9時20分までのBさんについて，ｙをｘの式で表しなさい。ただし，ｘの変域は求めなくてよい。
(３) AさんとBさんがすれちがったのは，P地点から何ｍの地点か，求めなさい。
(４) Cさんは9時ちょうどにP地点を出発して，2人と同じ道を自転車に乗って分速300ｍでＱ地点まで移動した。Ｃさんが出発してから2分後の地点に図書館があり，Ｃさんがその図書館に立ち寄ったので，9時12分にＡさんからＣさんまでの距離と，ＣさんからＢさんまでの距離が等しくなった。Ｃさんが図書館にいた時間は何分何秒か，求めなさい。
解答・解説
(１) 【正答 ７０】
980ｍの道のりを14分で歩いているので，
980÷14＝70
(２) 【正答 ー７０x＋１４００】
グラフの傾きは，(yの増加量)÷(xの増加量)で求めることができる。
傾きa＝(0ー980)／(20ー6)＝－70
切片bは，y＝－70x＋b に（20，0）を代入し求めることができる。
0＝－70×20＋b ⇔ b＝ー1400
よって，y＝－70x＋1400 ー①
(３) 【正答 ７００】
9時から9時14分までのAさんについて，ｙをｘの式で表すと，（２）と同様に求めればいいので，
傾き＝(980ー0)／(14ー0)＝70
原点を通っているので，切片は0
よって，y＝70x ー②
①と②のグラフの交点を求めればよいので，①に②に代入して，
70x＝－70x＋1400
⇔140x＝1400
⇔x＝10
これを，②に代入して，
y＝70×10＝700
(４) 【正答 ９分４０秒】
9時12分の時のAさんのP地点からの距離は，
②にx＝12を代入して，
y＝70×12＝840 ー③
9時12分の時のBさんのP地点からの距離は，
①にx＝12を代入して，
y＝－70×12＋1400＝560 ー④
③，④から，AさんとＢさんの位置の中間距離は，
(840ー560)／２＝140
よって，Ｐ地点からの距離は，
560＋140＝700 となる。
また，図書館はＰ地点から，300×２＝600ｍ の距離にあるのので，
図書館から700ー600＝100ｍ進んだ位置が，ＡさんからＣさんまでの距離と，ＣさんからＢさんまでの距離が等しくなる位置である。
Ｃさんは，分速300ｍで進むので，100ｍ進むのにかかる時間は，
100／300＝1／3分＝20秒
よって，求める時間は，図書館までの移動にかかった時間と，図書館から100ｍ進むのにかかった時間をひけばいいので，
12分ー2分ー20秒＝9分40秒
大問3
問題文
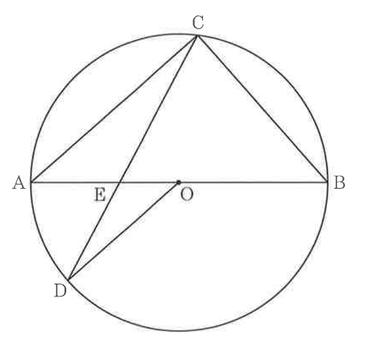
図のように，長さ8㎝の線分ABを直径とする円Oの周上に，点CをAC＝6cmとなるようにとる。
次に，点Cを含まない弧AB上に，点DをAC//DOとなるようにとり，線分ABと線分ＣＤの交点をＥとする。
(１) △ACE∽△ODEを次のように証明した。
ⅰ，ⅱに当てはまるものを，あとのア～カからそれぞれ一つ選んでその符号を書き，この証明を完成させなさい。
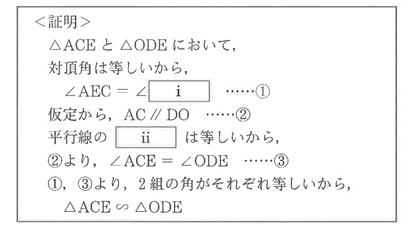
(２) 線分BCの長さは何㎝か，求めなさい。
(３) △ACEの面積は何㎠か，求めなさい。
(４) 線分DEの長さは何㎝か，求めなさい。
解答・解説
(１) 【正答 ⅰ: ウ ⅱ: オ】
対角は等しいので，ⅰはウとなる。
(２) 【正答 ２√７】
直径ABの円周角なので，∠ACB＝90°
三平方の定理より，
8²＝6²＋BC²
⇔BC²＝28
⇔BC＝2√7
(３) 【正答 ９√７ /５】
線分ODは半径なので，4㎝
△ACE∽△ODEより，
△ACE：△CEO＝AE：OE＝AC：OD＝6：4＝2：3
よって，
△ACE＝△AOC×5／3 ＝ (△ABC／2)×5／3
＝ ( 6×2√7／2)×5／3
＝9√7 / 5
(４) 【正答 ４√１４/５】
直線DOと線分BCが交わる点をHとする。
AC//DOより，∠CHD＝90° ー①
また△ABCにおいて，
AC//OH，BO：AB＝4：8＝1：2より，
BO：AB＝BH：BC＝OH：AC＝1：2
OH＝3，CH＝√7 ー②
△CDHにおいて，①，②から
CH＝√7，DH＝7，∠CHD＝90° と分かるので，
三平方の定理より，
CD²＝(√7)²＋7²＝56
CD＝2√14
また，CE：ED＝3：2から
CE＝2√14×3／2＝４√１４/５
大問4
問題文
図のように，関数 y＝ax² のグラフ上に2点A，Bがあり，関数 y＝x²/2のグラフ上に2点C，Dがある。点Aと点Cのｘ座標は2，点Ｂのｘ座標は4，点Ｃと点Ｄはｙ座標が等しい異なる２点である。 また、関数 y＝ax² で，ｘの値が2から4まで増加するときの変化の割合は3/2である。
次の問いに答えなさい。
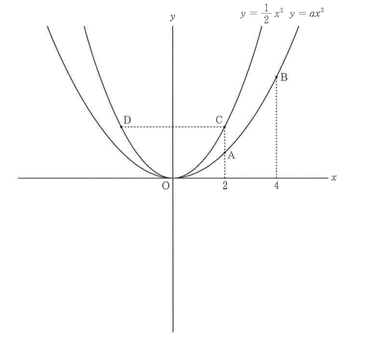
問1：点Ｃのｙ座標を求めなさい。
問2：aの値を求めなさい。
問3：直線ＡＢ上に，点Ｄとｘ座標が等しい点Ｅをとる。
① 点Ｅ座標をを求めなさい。
② 四角形ＡＣＤＥを，直線ＣＤを軸として１回転させてできる立体の体積は何㎤か，求めなさい。ただし，座標軸の単位の長さは１㎝とし，円周率はπとする。
解答・解説
(１) 【正答 ２】
点Cは，関数 y＝x²/2上にあり，x座標が2なのでこれを代入して，
y＝2²/2＝2
(２) 【正答 １/４】
x＝2を代入すると， y＝a×2²＝4a
x＝4を代入すると， y＝a×4²＝16a
よって，ｘの値が2から4まで増加するときの変化の割合は，
(16aー4a)／4ー2＝12a／2＝6a
これが3/2なので，
6a＝3/2
⇔a＝1/4
(３) 【正答 ①(ー２，ー５)】
直線ABの式は，A(2，１)，B(4，4)より，
yー1＝(4ー1)／(4ー2) ×(x－2)
y＝3x/2 ー2 ー①
これに，x＝ー2を代入して，
y＝3×(ー2)/2 ー2＝ー5
よって，Eの座標は，(ー2，ー5)
【正答 ②７６π】
直線AEと直線CDの交点を点Fとする。
点Fの座標は，①の式に，y＝2を代入すればいいので，
2＝3x/2 ー2
⇔x＝8/3
また，
（四角形ACDEを，直線CDを軸として１回転させてできる立体の体積）
＝（三角錐DEF）ー（三角錐ACF）
＝（(2ー(－5))²×π×(8/3ー(ー2))×1/3）ー（(2ー1)²×π×(8/3ー2)×1/3）
＝686π/9 ー2π/9 ＝76π
大問5
問題文
異なる３つの袋があり，1つの袋にはA，B，C，D，Eの5枚のカードが，残りの2つの袋にはそれぞれB，C，Dの3枚のカードが入っている。
それぞれの袋から1枚のカードを同時に取り出すとき，次の問いに答えなさい。
ただし，それぞれの袋において，どのカードが取り出されることも同様に確からしいものとする。
(１) 取り出したカードの文字が3枚とも同じ文字となる取り出し方は何通りあるか，求めなさい。
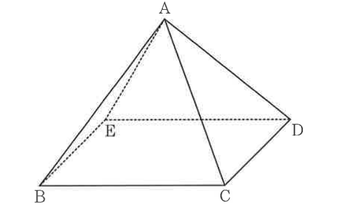
(２) 図のように，すべての辺の長さが2㎝である正四角すいABCDEがある。
それぞれの袋から取り出したカードの文字に対応する正四角すいの点に印をつけ，印がついた点を結んでできる図形Xを考える。異な る3点に印がついた場合，図形Xは三角形，異なる2点に印がついた場合，図形Xは線分，１点に印がついた場合，図形Xは点となる。
① 図形Xが，線分BCとなるカードの取り出し方は何通りあるか，求めなさい。
② 図形Xが線分となり，それを延長した直線と辺ABを延長した直線がねじれの位置にあるカードの取り出し方は何通りあるか，求めなさい。
③ 図形Xが，面積が2㎠の三角形となる確率を求めなさい。
解答・解説
(１) 【正答 3】
それぞれの袋から，B，C，Dのいずれかを同時に取り出すのは3通りとなる。
(２) 【正答 ①６】
それぞれの袋からの取り出し方は，
(5枚カードが入っている袋，3枚カードが入っている袋A，3枚カードが入っている袋B)
＝(B，B，C)，(B，C，B)，(B，C，C)，(C，B，B)，(C，B，C)，(C，C，B)
の６通り考えられる。
【正答 ②８】
辺ABを延長した直線とねじれの関係にある辺は，辺CD，辺EC，辺EDである。
図形Xが線分CDとなるためには，(２)と同様に考えて，6通り。
図形Xが線分ECになるためには，5枚のカードが入っている袋からE，ほかの2つの袋からCを取り出さなければいけないので，1通り。
線分EDも同様に考えて，1通り。
よって，6＋1＋1＝8通り
【正答 ③１４/４５】
組み合わせ方は全部で，5×3×3＝45通り
面積が2㎠となる三角形は，△ABD，△ACE，△BCD，△BCE，△BDE，△CDEの6つ。
このうち，△ACEは図形Xがとり得ない形なので残りの5つを考える。
図形Xが△ABDとなる取り出し方は，
(5枚カードが入っている袋，3枚カードが入っている袋A，3枚カードが入っている袋B)
＝(A，B，D)，(A，D，B)
の2通り。
図形Xが△BCDとなる取り出し方は6通り。
図形Xが△BCEとなる取り出し方は，
(5枚カードが入っている袋，3枚カードが入っている袋A，3枚カードが入っている袋B)
＝(E，B，C)，(E，C，B)
の2通り。
△BDE，△CDEも△BCEと同様に考えて，2通りずつ。
図形Xが，面積が2㎠の三角形となる組み合わせ方は，2＋6＋2＋2＋2＝14
よって，１４/４５
大問6
問題文
あきらさんとりょうさんは，東京2020オリンピックで実施されたスポーツクライミングについて話をしている。
2人の会話に関して，あとの問いに答えなさい。
(１) 表の［ア］にあてはまる 数を書きなさい。
(２) 2人は，総合順位やポイントについて話を続けた。［①］，［③］にあてはまる数，［②］にあてはまる式をそれぞれ求めなさい。ただし，ｎは0＜ｎ＜１０を満たす整数とし，ポイントの差は大きい方から小さい方をひいて求めるものとする。また，各種目について同じ順位の選手はいないものとする。
(３) Ａ選手，Ｂ選手を含む20人の選手が，東京オリンピックと同じ3種目で実施されたスポーツクライミングの大会に出場した。この大会の総合順位は，東京オリンピックと同様に，3種目の順位をかけ算して算出したポイントを用いて決定したものとし，Ａ選手，Ｂ選手の種目の順位やポイントについて次のことが分かった。
このとき，総合順位はＡ選手，Ｂ選手のどちらかの選手が下位であったか，求めなさい。また，その選手の残りの2種目の順位を求めなさい。ただし，各種目について同じ順位の選手はいないものとする。
解答・解説
(１) 【正答 ４２】
各種目の順位をかければいいので，
3×2×７＝42
(２) 【正答 ①４】
それぞれの平均順位は，
1位の選手 (1＋7＋4)／3＝4
2位の選手 (6＋1＋5)／3＝4
3位の選手 (7＋5＋1)／3＝4.33
4位の選手 (2＋3＋6)／3＝3.66
5位の選手 (3＋2＋7)／3＝4
6位の選手 (4＋6＋2)／3＝4
7位の選手 (5＋4＋3)／3＝4
となるので，4位の選手が１位になる。
【正答 ②１０ｎ²】
それぞれの順位をかけ合わせればいいので，
10×10×10ー(10＋n)×10×(10ーn)＝10³ー10n²ー10³＝10n²
【正答 ③８１０】
0＜ｎ＜１０より，
n＝9の時差が最大になるので，
10×9²＝810
(３) 【正答 A選手】
【正答 ６位，１７位 (順不同)】
401～410の間で，
4で割り切れるものは，404，408
15で割り切れるものは，405
このことからB選手は405ポイント，
404÷4＝101
408÷4＝102 となり101は素数なので，A選手は408ポイントと分かる。
よって，A選手の方が下位になる。
また，A選手は合計408ポイントで１種目4位を取っているので，残り2種目の順位の積は，
408÷4＝102
20以下の組み合わせで，積が102となるのは6，17の組み合わせのみとなる。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、兵庫県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
