【東京都】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
東京都の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の各問いに答えよ。
問1
$-8+6^2 \div 9$を計算せよ。
問2
$\frac{7a+b}{5}-\frac{4a-b}{3}$を計算せよ。
問3
$(\sqrt{6}-1)(2\sqrt{6}+9)$を計算せよ。
問4
一次方程式$4(x+8)=7x+5$を解け。
問5
連立方程式$2x+3y=1…①,8x+9y=7…②$を解け。
問6
二次方程式$2x^2-3x-6=0$を解け。
問7
次の【あ】【い】に当てはまる数字をそれぞれ答えよ。
袋の中に、赤玉が1個、白玉が1個、青玉が4個、合わせて6個の玉が入っている。
この袋の中から同時に2個の玉を取り出すとき、2個とも青玉である確率は、$\frac{【あ】}{【い】}$である。
ただし、どの玉が取り出されることも同様に確からしいものとする。
問8
次の【う】【え】に当てはまる数字をそれぞれ答えよ。
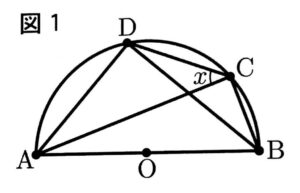
次の図1で、点Oは、線分ABを直径とする半円の中心である。
点Cは、弧AB上にある点で、点A、点Bのいずれにも一致しない。
点Dは、弧AC上にある点で、点A、点Cのいずれにも一致しない。
点Aと点C、点Aと点D、点Bと点C、点Bと点D、点Cと点Dをそれぞれ結ぶ。
∠BAC=20°、∠CBD=30°のとき、xで示した∠ACDの大きさは、【う】【え】度である。
問9
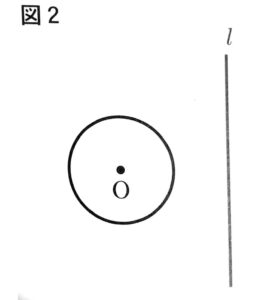
次の図2で、円Oと直線lは交わっていない。
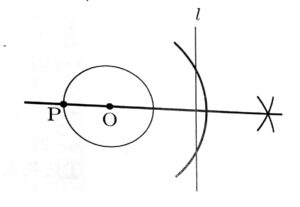
円Oの周上にあり、直線lとの距離が最も長くなる点Pを、定規とコンパスを用いて作図によって求め、点Pの位置を示す文字Pもかけ。
ただし、作図に用いた線は消さないでおくこと。
解答・解説
問1 $-4$
計算の順序を間違えないようにしましょう。
$-8+36\div9=-8+4=-4$
問2 $\frac{a+8b}{15}$
通分をしてから求めます。
$\frac{3(7a+b)}{15}-\frac{5(4a-b)}{15}=\frac{21a+3b-20a+5b}{15}=\frac{a+8b}{15}$
問3 $3+7\sqrt{6}$
根号は2乗の形になると外に出すことができます。
$12+9\sqrt{6}-2\sqrt{6}-9=3+7\sqrt{6}$
問4 $9$
$4x+32=7x+5$
$-3x=-27$
$x=9$
問5 $x=2,y=-1$
①を3倍して加減法で求めます。
$6x-8x=3-7$
$-2x=-4$
$x=2$
これを①に代入して
$4+3y=1$
$y=-1$
問6 $\frac{3 \pm \sqrt{57}}{4}$
解の公式$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$を用います。
$x=\frac{-(-3) \pm \sqrt{(-3)^2-4\times2\times(-6)}}{2\times2}=\frac{3 \pm \sqrt{57}}{4}$
問7 【あ】2【い】5
全通りは15通り、青玉だけでるのは6通りなので
$\frac{6}{15}=\frac{2}{5}$
問8 【う】4【え】0
弧ACに対する円周角より、∠CBD=∠CAD=30°
弧AB（直径）に対する円周角より、∠ADB=90°
弧ADに対する円周角より、∠ACD=∠ABD=x°
△ADBに注目すると、∠DAC+∠CAB+∠ADB+∠ABD=180°となるので
$30+20+90+x=180$
$x=40$
問9 下図参照
大問2 証明問題
問題文
Sさんのクラスでは、先生が示した問題をみんなで考えた。
次の各問いに答えよ。
【先生が示した問題】
a,bを正の数とし、a>bとする。
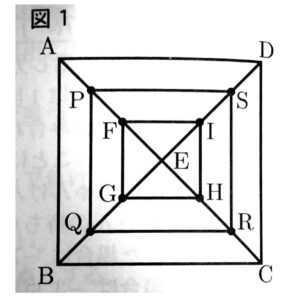
次の図1で、四角形ABCDは、1辺の長さがacmの正方形である。頂点Aと頂点C、頂点Bと頂点Dをそれぞれ結び、線分ACと線分BDの交点をEとする。
線分AE上にあり、頂点A、頂点Eのいずれにも一致しない点をFとする。
線分BE,線分CE,線分DE上にあり、EF＝EG＝EH＝EIとなる点をそれぞれG,H,Iとし、点Fと点G、点Fと点I、点Gと点H、点Hと点Iをそれぞれ結ぶ。
線分AF,線分BG,線分CH,線分DIの中点をそれぞれP,Q,R,Sとし、点Pと点Q、点Pと点S、点Qと点R、点Rと点Sをそれぞれ結ぶ。
線分FGの長さをbcm、四角形PQRSの周りの長さをlcmとするとき、lをa,bを用いた式で表しなさい。
問1
【先生が示した問題】で、lの値をa,bを用いてl=【】cmと表すとき、【】に当てはまる式を、次のア～エのうちから選び、記号で答えよ。
ア：$2a+2b$
イ：$\frac{a+b}{2}$
ウ：$\frac{a-b}{2}$
エ：$2a-2b$
Sさんのグループは、【先生が示した問題】をもとにして、次の問題を考えた。
【Sさんのグループが作った問題】
a,bを正の数とし、a>bとする。
次の図2は、線分OA上にあり、点O、点Aのいずれにも一致しない点をB、線分ABの中点をMとし、線分OA、線分OB、線分OMをそれぞれ点Oを中心に反時計回りに90°回転移動させてできた図形である。
図2において、線分OAの長さをacm、線分OBの長さをbcm、線分OMを半径とするおうぎ形から、線分OBを半径とするおうぎ形を除いた残りの図形の面積をS㎠とするとき、S=(a-b)lとなることを確かめてみよう。
問2
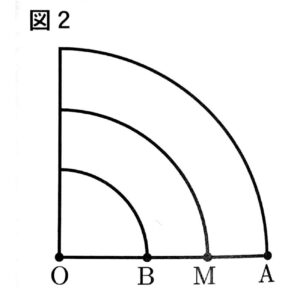
【Sさんのグループが作った問題】でlをa,bを用いた式で表し、S=(a-b)lとなることを証明せよ。ただし、円周率はπとする。
解答・解説
問1 ア
台形ABGFで、次の図のように4点J,K,L,Mを作る。
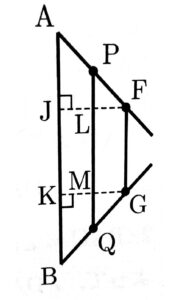
$AB=a,FG=b$なので、
$AJ=\frac{AB-FG}{2}=\frac{a-b}{2}$
中点連結定理より$PL=\frac{1}{2}AJ=\frac{a-b}{4}$
以上より、
$PQ=PL+LM+MQ=\frac{a-b}{4}+b+\frac{a-b}{4}=\frac{a+b}{2}$
$l=4PQ=4\times\frac{a+b}{2}=2a+2b$
問2 下記参照
線分OMの長さは$\frac{a+b}{2}$なので、
$l=\frac{1}{4}\times2π\times\frac{a+b}{2}=\frac{1}{4}π(a+b)$
よって、
$(a-b)l=(a-b)\times\frac{1}{4}π(a+b)=\frac{1}{4}π(a+b)(a-b)…①$
線分OAを半径とするおうぎ形の面積は、$\frac{1}{4}πa^2$
線分OBを半径とするおうぎ形の面積は、$\frac{1}{4}πb^2$
よって、
$S=\frac{1}{4}πa^2-\frac{1}{4}πb^2=\frac{1}{4}π(a^2-b^2)=\frac{1}{4}π(a+b)(a-b)…②$
①、②より、$S=(a-b)l$
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 一次関数
問題文
次の図1で、点Oは原点、点Aの座標$(3,-2)$であり、直線lは一次関数$y=\frac{1}{2}x+1$のグラフを表している。
直線lとx軸との交点をBとする。
直線l上にある点をPとし、2点A,Pを通る直線をmとする。
次の各問いに答えよ。
問1
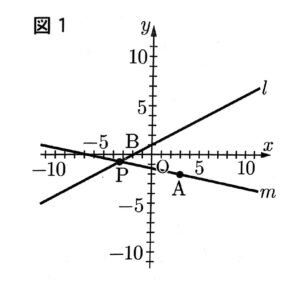
点Pのy座標が-1のとき、点Pのx座標を、次のア～エのうちから選び、記号で答えよ。
ア：$-1$
イ：$-\frac{5}{2}$
ウ：$-3$
エ：$-4$
問2
次の①と②にあてはまる数を、下のア～エのうちから選び、記号で答えよ。
線分BPがy軸により二等分されるとき、直線mの式は、$y=①x+②$である。
①
ア：$-6$
イ：$-4$
ウ：$-3$
エ：$-\frac{5}{2}$
②
ア：$5$
イ：$\frac{11}{2}$
ウ：$7$
エ：$10$
問3
次の図2は、図1において、点Pのx座標が０より大きい数であるとき、y軸を対称の軸として点Pと線対称な点をQとし、点Aと点B、点Bと点Q、点Pと点Qをそれぞれ結んだ場合を表している。
△BPQの面積が△APBの面積の2倍であるとき、点Pのx座標を求めよ。
解答・解説
問1 エ
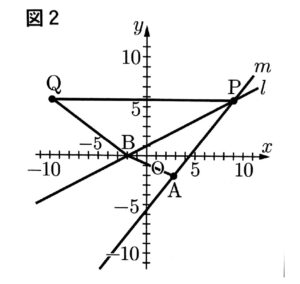
直線lの式に$y=-1$を代入すればよいので
$-1=\frac{1}{2}x+1$
$\frac{1}{2}x=-2$
$x=-4$
問2 ①イ ②エ
線分BPがy軸によって二等分されるためには、2点B,Pはy軸から等しい距離にあればよい。点Bのx座標は-2なので、Pのx座標は2である。よって、点Pの座標は問1と同様に求めると$P(2,2)$
これで点Aと点Pの座標が求まったので、mの式を$y=ax+b$として、それぞれの座標を代入し、連立方程式を解くと$a=-4,b=10$となるので、mの式は$y=-4x+10$となる。
問3 ９
点Aを通り直線lに平行な直線とx軸との交点をA’とする。
AA’の式を$y=\frac{1}{2}x+c$とすると、
$-2=\frac{1}{2}\times3+c$
$c=-\frac{7}{2}$
A’のy座標は0なので、
$0=\frac{1}{2}x-\frac{7}{2}$
$x=7$
よって、$A'(7,0)$
ここで、PQ//A’Bより、△BPQ：△APB＝PQ：A’B…①
点Pのx座標をtとすると、点Qのx座標は-tと表せる。
よって、$PQ＝t-(-t)=2t,A’B=7-(-2)=9$
△BPQの面積は△APBの面積の2倍なので、
△BPQ：△APB＝２：１…②
①、②より
$PQ:A’B=2t:9=2:1$
$t=9$
大問4 平面図形
問題文
次の図1で、四角形ABCDは、AD//BC,AB＝DC,AD＜BCの台形である。
点Pは、辺AB上にある点で、頂点A、頂点Bのいずれにも一致しない。
点Qは、辺BC上にある点で、頂点B、頂点Cのいずれにも一致しない。
頂点Aと点Q、頂点Dと点Pをそれぞれ結ぶ。
次の各問いに答えよ。
問1
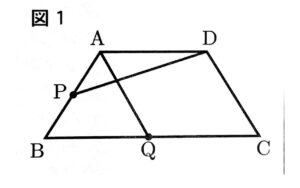
図1において、AQ//DC,∠AQC＝110°,∠APD＝a°とするとき、∠ADPの大きさを表す式を、次のア～エのうちから選び、記号で答えよ。
ア：$(140-a)$度
イ：$(110-a)$度
ウ：$(70-a)$度
エ：$(40-a)$度
問2
次の図2は、図1において、頂点Aと頂点C、頂点Dと点Q、点Pと点Qをそれぞれ結び、線分ACと線分DPとの交点をR、線分ACと線分DQとの交点をSとし、AC//PQの場合を表している。
次の①、②に答えよ。
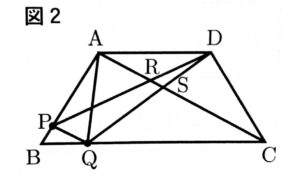
①△ASD∽△CSQであることを証明せよ。
②次の【お】【か】【き】に当てはまる数字をそれぞれ答えよ。
図2において、AP:PB＝3:1、AD:QC＝2:3のとき、△DRSの面積は、台形ABCDの面積の$\frac{【お】}{【か】【き】}$倍である。
解答・解説
問1 ウ
四角形AQDCは平行四辺形なので、∠QAC＝180-110＝70°
そして△ABQは二等辺三角形であり、∠AQB＝180-∠AQC＝180-110＝70°となる。よって、∠BAQ＝60°
△APDに注目すると、∠ADP＝180-（∠APD+∠PAD）＝180-（∠APD+∠PAQ+∠QAD）＝（70-a）度
問2 ①下記参照 ②【お】1【か】3【き】0
①△ASDと△CSQにおいて
対頂角は等しいので、∠ASD＝∠CSQ…①
AD//BCより、平行線の錯角は等しいので、
∠ADS＝∠CQS…②
①、②より、2組の角がそれぞれ等しいので、
△ASD∽△CSQ
②△BACにおいて、PQ//ACより、
BQ:QC＝BP:PA＝1：3
AD:QC＝2：3
よって、AD:BQ＝2：1
AD:BC＝AD:（BQ+QC）＝2：4＝1：2
△ASD∽△CSQより、DS：QS＝AD:CQ＝2：3
よって、DS:DQ＝DS：（DS+SQ）＝2：5
△DPQにおいて、RS//PQより、RS:PQ＝2：5
RS＝$\frac{2}{5}$PQ…①
△BCAにおいて、PQ:AC＝BP:BA＝BP:（BP+PA）＝1：4
AC＝4PQ…②
①、②より、RS：AC＝$\frac{2}{5}$PQ：4PQ＝1：10
△DRS:△DAC＝1：10
よって、△DRS＝$\frac{1}{10}$△DAC…③
また、△DAC：台形ABCD＝△DAC：（△DAC+△BAC）＝1：3
よって、台形ABCD＝3△DAC…④
③、④より、△DRS：台形ABCD＝$\frac{1}{10}$△DAC：3△DAC＝1：30
これらより、△DRSの面積は、台形ABCDの面積の$\frac{1}{30}$倍
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 空間図形
問題文
次の図1に示した立体A-BCDは、1辺の長さが6ｃｍの正四面体である。
辺ACの中点をMとする。
点Pは、頂点Aを出発し、辺AB、辺BC上を毎秒1ｃｍの速さで動き、12秒後に頂点Cに到着する。
点Qは、点Pが頂点Aを出発するのと同時に頂点Cを出発し、辺CD、辺DA上を点Pと同じ速さで動き、12秒後に頂点Aに到着する。
点Mと点P、点Mと点Qをそれぞれ結ぶ。
次の各問いに答えよ。
問1
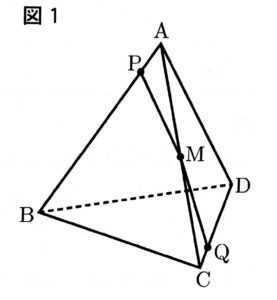
次の【く】【け】に当てはまる数字をそれぞれ答えよ。
図1において、点Pが辺AB上にあるとき、MP+MQ＝ｌcmとする。
ｌの値が最も小さくなるのは、点Pが頂点Aを出発してから$\frac{【く】}{【け】}$秒後である。
問2
次の【こ】【さ】に当てはまる数字をそれぞれ答えよ。
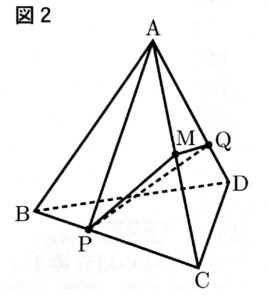
次の図2は、図1において、点Pが頂点Aを出発してから8秒後のとき、頂点Aと点P、点Pと点Qをそれぞれ結んだ場合を表している。
立体Q-APMの体積は、$【こ】\sqrt{【さ】}cm^3$である。
解答・解説
問1 【く】３ 【け】２
ｌの値が最も小さくなるのは、AB⊥PQとなるとき。
△MAPは30°、60°、90°の直角三角形でAM=3より、
$AP=\frac{1}{2}AM=\frac{3}{2}$
問2 【こ】４ 【さ】２
8秒後なので、BP=2、PC=4
ここで、△ABP：△ACP＝１：２、△ABC：△ACP＝３：２、△ABC＝$\frac{3}{2}$△ACP…①
また、AM＝CMより、△AMP＝$\frac{1}{2}$△ACP…②
よって、①、②より
△AMP：△ABC＝$\frac{1}{2}$△ACP：$\frac{3}{2}$△ACP＝１：３
△ABC＝$6\times3\sqrt{3}\times\frac{1}{2}=9\sqrt{3}$
△AMP＝$\frac{1}{3}△ABC=3\sqrt{3}$
∠BACと∠ABCの二等分線の交点をIとする。
△AIMは30°、60°、90°の直角三角形になるので、
AI＝$\frac{2}{\sqrt{3}}AM=\frac{2}{\sqrt{3}}\times3=2\sqrt{3}$
△DAIは∠I＝90°より、
DI＝$\sqrt{DA^2-AI^2}=\sqrt{6^2-(2\sqrt{3})^2=2\sqrt{6}}$
△DAIにおいて、QからIDに平行な直線をひきAIとの交点をRとすると
AQ：RQ＝AD：ID
$4:RQ=6:2\sqrt{6}$
$RQ=\frac{4\sqrt{6}}{3}$
ここで、DI⊥△AMPより、RQ⊥△AMP
つまり、RQは立体Q-APMの高さと考えてよい。
よって、その体積は
$\frac{1}{3}\times△AMP\times RQ=\frac{1}{3}\times3\sqrt{3}\times\frac{4\sqrt{6}}{3}=4\sqrt{2}$
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、東京都にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
