【京都府】平成31年度/2019年度入学者高校入試選抜試験：数学の解説
京都府の2019年3月実施の平成31年度（2019年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
京都府の数学問題は、難易度としては難しい。小問集合と数列のような規則性を問う問題が必ず出るのが特徴です。
時間配分の仕方が肝になるので、時間を計りながら過去問に挑戦してみるといいかもしれません。
【京都府】平成31年度一般入学者選抜の過去問はこちらから
数学(前期)の過去問題はこちら＞＞
数学(中期)の過去問題はこちら＞＞
【前期】大問1：小問集合
問1：正負の数
問1：{5-(-2²)}÷(3/4)² を計算する問題です。
【・答え「16」】
与式={5-(-4)}÷9/16
=9×16/9=16
問2：文字と式
問2：(7x-1)/5-x+2 を計算する問題です。
【・答え「(2x+9)/5」】
与式=(7x-1)/5-(5x-10)/5
=(2x+9)/5
問3：平方根
問3：(3-√5)²+10/√5 を計算する問題です。
【・答え「14-4√5」】
与式=9-6√5+5+10/√5
=9-6√5+5+10/√5×√5/√5
=14-4√5
問4：代入・二次方程式
問4：a=30，b=-23のとき、(a-2b)²-2(a-2b)-24 を計算する問題です。
【・答え「5600」】
a-2b=Aとすると、与式=A²-2A-24=(A-6)(A+4)
a-2bに、a=30，b=-23をそれぞれ代入すると76になる。
a-2b=Aなので(76-6)(76+4)=70×80=5600
問5：二次方程式
問5：3x²-3x-2=0 を計算する問題です。
【・答え「(3±√33)/6」】
解の公式を使って解く。
x={3±√(-3)²-4×3×(-2)}/6
=(3±√9+24)/6=(3±√33)/6
問6：立体図形
問6：球Aの表面積が球Bの表面積の9倍で、球Bの半径が4cmであるときの球Aの半径を求める問題です。
【・答え「12cm」】
「球の表面積」=4πr²で表すことができる。
球Bの表面積=4×π×4²=64π
球Aはその9倍の表面積なので球Aの表面積=9×64πとなり、
これを公式に当てはめると、
4πr²=9×64π
r²=(3×4)²
r²=±12 r>0なので半径は12cmとなる。
問7：二次関数
問7：関数y=-2x² において、xの変域が-2≦x≦pのときのyの変域が-8≦y≦-1/18である。このときのpの値を求める問題です。
【・答え「p=-1/6」】
-2x²=-1/18 -2x²×1/2=-1/18×1/2 x²=±1/6
yの変域が-8≦y≦-1/18であることから、x<0なのでp=-1/6となる。
問8：不等式
問8：ある物体の重さは3.1gである。この数値が小数第2位を四捨五入して得られた数値である場合、この物体の重さの真の値をaとして、aの範囲を【3.05≦a[A][X]】と不等式で表すとき、AとXに当てはまる不等号と数を語群から選ぶ問題です。
【・答え「A…ア X…ク」】
3.14は小数第2位を四捨五入すると3.1となるが、3.15の小数第2位を四捨五入すると3.2になる。
仮に、3.149の場合は3.1となるので3.15を含めない、「3.05≦a<3.15」が答え。
問9：平行と合同
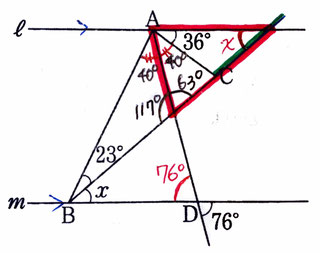
問9：∠xの大きさを求める問題です。
【・答え「∠x=41°」】
線分BCを点Cの方に延長し、直線Lと交わるようにする。
∠D=76°から、赤で囲った三角形の∠Aの部分も76°となり、
76°-36°=40°なので、直線mは∠BACを40°ずつに二等分していることがわかる。
あとは三角形の内角の和は180°であることから順番に計算していくと、
赤で囲った三角形の直線BCと直線Lの交点の部分の角は問題の∠xと錯角の関係なので、∠x=41°
【前期】大問2：確率
6つの玉と、2つのさいころ、1から6の数が書かれた6つの箱を使います。2つのさいころを同時に投げ、出た目の数が同じときはその数が書かれた1つの箱に玉を1個入れ、さいころの目が異なるときは出た目の数が書かれたそれぞれの箱と、玉を入れた2つの箱の間に箱があれば間にある箱すべてに玉を1個ずつ入れる操作をするときの確率について答える問題です。
問1：
問1：6個の箱すべてに玉が入る確率を求める問題です。
【・答え「1/18」】
確率を求める問題では、まず全部で何通りのパターンがあるかを考える。
ふたつのさいころを同時に投げるので、さいころの目の出方は「1」～「6」で6通り。
ふたつあるので、6×6=36で36通りある。
6つすべての箱に玉が入るのは、さいころで「1」と「6」が同時に出たときのみなので
「1」と「6」、「6」と「1」の2通りなので 2/36=1/18となる。
問2：
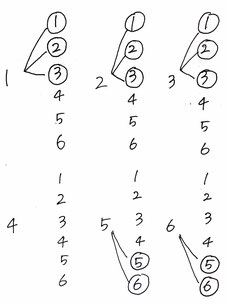
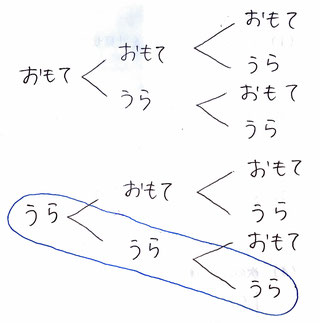
問2：4が書かれた箱に玉が入らない確率を求める問題です。
【・答え「13/36」】
4が書かれた箱に玉が入らないのは、ふたつのさいころの目が「4」をまたがないときなので樹形図で表すと画像のようになる。よって、13/36が答え。
【前期】大問3：関数
問1：
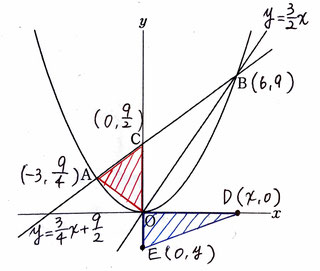
問1：aの値を求める問題です。
【・答え「a=1/4」】
直線OBは原点を通り、傾きが3/2の直線なのでy=3/2xであるということが言える。
点Bは関数y=ax²上を通るので、y=3/2×6=9から、Bの座標は(6，9)となる。
よって、9=a×6² 9=36a a=1/4
問2：
問2：直線ABの式を求める問題です。
【・答え「y=3/4a+9/2」】
問1より、点Aのy座標はy=1/4×(-3)²=9/4 となり、点AとBの座標はそれぞれ、A(-3，9/4) B(6，9)であると言える。
直線ABをy=ax+bの式に当てはめ、連立方程式 9/4=-3a+b，9=6a+bを解く。
9/4=-3a+b…①，9=6a+b…②とすると、
①-②は9/4-9=-9a -27/4=-9a a=3/4…③
③を②に代入すると、
9=6×3/4+b 9=9/2+b b=9-9/2 b=9/2
よって、直線ABの式は y=3/4x+9/2
問3：
問3：x軸上にx座標が正である点Dと、点Dを通り傾きが6/25である直線とy軸の交点Eをとる。△OCA=△OEDであるときの点D，Eそれぞれの座標を求める問題です。
【・答え「D（15/2，0）E（0，-9/5）」】
傾きが6/25であることから、直線DEの式はy=6/25x+bと表すことができ、
点Dはy=0のときなので、
6/25+b=0 6/25x=-b x=-25/6b となる。
よってD(-25/6b，0)，E(0，b)になるので、
△OED=1/2×b×(-25/6b)=-25/12b² となり、
△OED=△OCAのときなので、-25/12b²=27/4 b²=27/4×(-12/25) b²=81/25 b²=(9/5)²
b=±9/5となり、b<0なので、b=-9/5
x=-25/6×(-9/5) x=15/2なので、D（15/2，0）E（0，-9/5）
【前期】大問4：空間図形
問1：
問1：三角錐ABCEの体積を求める問題です。
【・答え「72cm³」】
緑色で示した部分が三角錐ABCEである。
三角錐の体積は(底面積)×(高さ)×1/3で求めることができる。
底面である△ABCの面積は 6√2×6√2×1/2=36(cm²)
よって、三角錐ABCEの体積は
36×6×1/3=72(cm³)
問2：
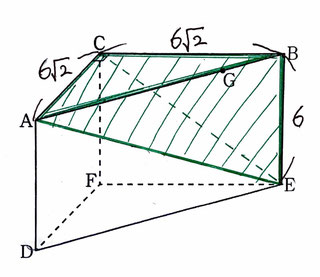
問2：線分EGの長さ、△CEGの面積を求める問題です。
【・答え「EG=3√5(cm) △CEG=9√6(cm²)」】
＊線分EG
三平方の定理を使って、線分ABの長さを求めます。(直角二等辺三角形の辺の比を使って求めることもできます)
AB=√{(6√2)²+(6√2)²}=√144=12
AG：GB=3：1なので、AG=9，GB=3
再び三平方の定理を使って線分EGの長さを求めます。
EG=√6²+3²=√45=3√5(cm)
＊△CEG
ピンク色で示した部分が△CEGである。
CEは長方形CBEFの対角線なので、三平方の定理を使うと
CE=√{(6√2)²+6²}=√108=6√3(cm)となる。
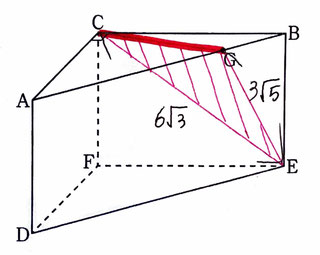
CGについては立体から抜き出すと画像の赤線の部分になる。
頂点CからABに向かって垂線を引き、交点をMとするとCM=6，MG=3なので、CG=√6²+3²=√45=3√5となる。
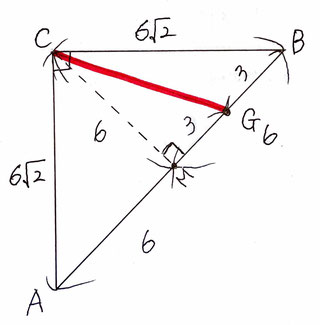
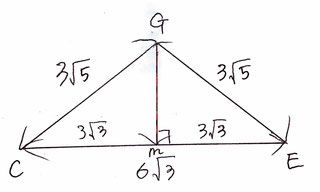
△CEGを抜き出すとこのようになり、Gm=√{(3√5)²-(3√3)²}=√18=3√2なので、
△CEGの面積は、6√3×3√2×1/2=9√6(cm²)となる。
問3:
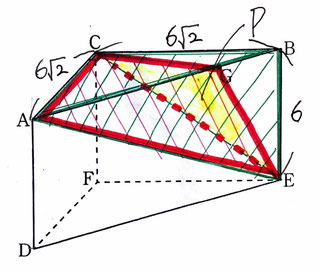
問3：3点C，E，Gを通る平面をPとするときの点Aと平面Pとの距離を求める問題です。
【・答え「3√6(cm)」】
赤色で示した三角錐ACGEを、△ACGを底面として考えると、
体積はABがAG：GB=3：1となっているので、
問1で求めた三角錐ABCE(緑色で示した部分)=72cm³より、
72×3/4=54(cm³)となる。
次に、三角錐ACGEを△CEGつまり点Pを底面、高さをhとして考えると、
問2より、9√6×h×1/3=54となり、これを解くとh=3√6となる。
高さ=平面Pと点Aの距離なので、3√6が答え。
【前期】大問5：平面図形
問1：
問1：△ABD≡△ACFであることを証明する問題です。
【・答え「△ABDと△ACFで、
仮定より、AB=AC …①
∠DAB=∠BCA
AF//BCより、平行線の錯角は等しいから、∠FAC=∠BCA
よって、∠DAB=∠FAC …②
弧ABに対する円周角は等しいから、∠ABD=∠ACF …③
①、②、③から、1組の辺とその両端の角がそれぞれ等しいので、
△ABD≡△ACF】
問2：
問2：線分BDの長さを求める問題です。
【・答え「6√7(cm)」】
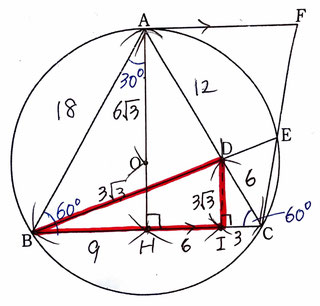
点Aから点Oに向かって線を引き、BCとの交点をHとする。
点Oは△ABCの重心なので、AO：OH=2：1だから
OH=3√3となり、AH=9√3であると言える。
△ABCが正三角形であること、
AHは△ABCの∠Aの二等分線であることから
△ABHについて∠B=60°、∠A=30°なので△ABHは辺の比が1：2：√3の三角定規であることがわかる。
よって、AB=18、BH=9となり、
AD=12なので、18-12=6で DC=6となる。
点DからBCに向かって垂線を引き、交点をIとすると、∠C=60°であることから△DICも辺の比が△ABHは辺の比が1：2：√3の三角定規であるということが言え、IC=3、DI=3√3となる。
赤色で示した△BDIについて考えると、BD=√(9+6)²+(3√3)²=√252=6√7(cm)
問3：
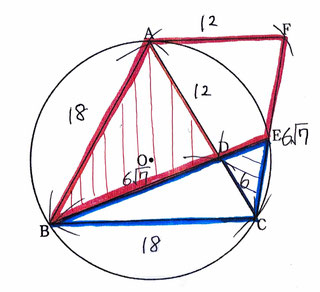
問3：四角形ABEFと△BCEの面積の比を最も簡単な整数の比で表す問題です。
【・答え「26：9」】
問1より、△ABD≡△ACFなので
CF=6√7となる。
また、△ABD∽△ECDなので
AB：EC=DB：DCということが言え、
18：EC=6√7：6 EC=18√7/7
CF-EC=EFなので
EF=6√7-18√7/7=(42√7-18√7)/7=24√7/7となる。
CE：EF=18√7/7：24√7/7 CE：EF=3：4 …①
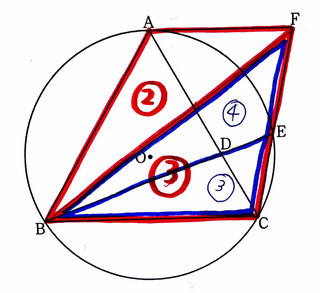
(i)△ABFと△BCF(赤色で示した部分)について考える
二つは底辺が異なり、高さが等しい三角形であるので、
底辺の比が面積の比になる。
△ABFにおけるAFは12cm、△BCFにおけるBCは18cmなので
面積比も△ABF：△BCF=12：18=2：3となる。
(ii)△BCEと△BEF(青色で示した部分)について考える
二つは①から底面が3：4で高さが等しい三角形であるので、
面積比も同じく3：4となる。
△BCFを21として考えると、△ABFは14となり、
△BEFは12、△BCEは9となる。
よって四角形ABEFは14+12=26なので 四角形ABEFと△BCEの面積比は26：9
【前期】大問6：規則性
問1：
問1：m=8において、残ったカードが4枚になるまで操作を繰り返し行うとき、残った4枚のカードのうち一番上のカードに書かれている数と、一番下のカードに書かれている数をそれぞれ求める問題です。
【・答え「一番上…2 一番下…8」】
問2：
問2：m=31において、残ったカードが16枚になるまで操作を繰り返し行うとき、残った16枚のカードのうち一番上に書かれている数と、一番下のカードに書かれている数をそれぞれ求める問題です。
【・答え「一番上…31 一番下…30」
問3：
問3：m=294において、残ったカードが73枚になるまで操作を繰り返し行うとき、残った73枚のカードのうち一番上に書かれている数と、一番下のカードに書かれている数をそれぞれ求める問題です。
【・答え「一番上…8 一番下…4」】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
【中期】大問1：小問集合
問1：正負の数
問1：(-6)²-4÷2 を計算する問題です。
【・答え「28」】
与式=36-16÷2=36-8=28
問2：文字と式
問2：(3a+1)/4-(4a-7)/6 を計算する問題です。
【・答え「(a+17)/12」】
与式={3(3a+1)}/12-{2(4a-7)}/12
=(9a-8a+3+14)/12=(a+17)/12
問3：平方根
問3：√27+√24×√8 を計算する問題です。
【・答え「11√3」】
与式=3√3+2√6×2√2
=3√3+4√12=3√3+8√3=11√3
問4：連立方程式
問4：連立方程式x=2+y，9x-5y=2 を計算する問題です。
【・答え「x=-2，y=-4」】
x=2+y…①，9x-5y=2…②とし、①を②に代入する。
9(2+y)-5y=2
18+9y-5y=2 y=-4…③
③を①に代入すると、x=2+(-4) x=-2
よって、x=-2，y=-4となる。
問5：多項式
問5：3a²-24a+28 を因数分解する問題です。
【・答え「3(a-4)²」】
与式=3(a²-8a+16)
=3(a-4)²
問6：一次関数
問6：直線y=-2/3x+5に平行で、点(-6，2)を通る直線の式を求める問題です。
【・答え「y=-2/3x-2」】
直線の式は「y=ax+b」で表すことができる
y=-2/3x+5と平行→直線の傾きは-2/3であるので、a=-2/3となる。
点(-6，2)を通るので、x=-6，y=2を代入すると、
2=-2/3×(-6)+b b=-2となる。
よって、y=-2/3x-2
問7：円
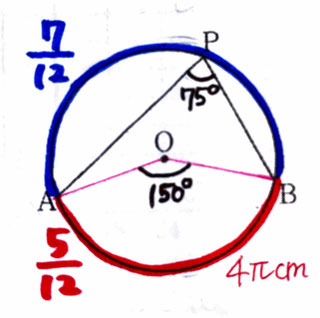
問7：円Oの周上に3点A，B，Pがあり、∠APB=75°である。円周角∠APBに対する弧ABの長さが4πcmであるときの、円Oの円周の長さを求める問題です。
【・答え「48/5πcm」】
ひとつの弧に対する中心角は円周角の2倍の大きさなので、∠APBの中心角は150°となる。
150°/306°=5/12より、弧AB(赤色の部分)=4πは円Oの円周全体の5/12の長さであることがわかり、
点Pを通る線分AB(青色の部分)は全体の7/12の長さであることがわかる。
よって、5：7=4π：AB 5AB=28π AB=28/5π となる。
よって、円Oの円周は28/5π+4π=48/5π(cm)
問8：確率
問8：3枚の硬貨を同時に投げるとき、少なくとも1枚は表が出る確率を求める問題です。
【・答え「7/8」】
「少なくとも1枚は表」=1-(すべて裏) ということである。
すべて裏が出るのは1/8の確率なので、1-1/8=7/8となる。
【中期】大問2：資料の分析と活用
ある中学校の通学時間に関する調査結果についての表と資料を読み取る問題です。
問1：
問1：表について、中央値がふくまれる階級の階級値を求める問題です。
【・答え「9分」】
中央値とは、調べようとする資料の値を大きさの順に並べたときの中央の値のことなので、
表では、3年1組は全員で29人いるので、14番目の生徒が中央値であるといえる。
0分以上6分未満の階級は5人、6分以上12分未満の階級は11人で、合わせると16人なので
中央値を含む階級は6分以上12分未満の階級であることがわかる。
階級値は階級の真ん中の値なので、(6+12)/2=9 となり、答えは9分である。
問2：
問2：資料をみて、3年2組のヒストグラムを完成させる問題です。
【・答え「画像を参照」】
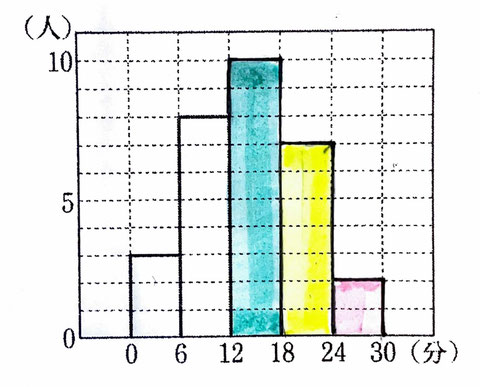
資料を見ると、通学時間が12分以上18分未満の生徒は10人、18分以上24分未満の生徒は7人、24分以上30分未満の生徒は2人なので画像のようになるのが正しい。
問3：
問3：資料および表から必ずいえるものを選択肢(ア)～(オ)のなかからすべて選ぶ問題です。
【・答え「イ，ウ，オ」】
(ア)誤り。通学時間が18分未満の生徒は、3年1組では5+11+6=22(人)で、3年2組では3+8+10=21(人)なので、3年1組の方が1人だけ多い。
(イ)通学時間が24分以上の生徒は、3年1組も3年2組も同じ2人なので、全体の人数が29人と少ない3年1組の方が割合が大きいため正しい。
(ウ)3年1組の通学時間が6分以上18分未満の生徒の人数は11+6=17(人)、3年2組の通学時間が12分以上24分未満の生徒の人数も10+7=17(人)なので正しい。
(エ)誤り。3年2組の生徒の中で、通学時間が最も短い生徒は通学時間が3分の生徒だが、3年1組の度数分布表のみでは0分以上6分未満の生徒が5人いることしかわからないので、3年2組の3分の生徒が最も短いとは限らない。
(オ)3年1組と3年2組の、通学時間が18分以上24分未満の生徒と24分以上30分未満の生徒をすべて合わせるとちょうど16人になり、3年2組の、通学時間が18分以上24分未満の生徒のうち最も小さい値は18分なので正しい。
【中期】大問3：空間図形
問1：
問1：立体Xの表面積、辺EFの長さを求める問題です。
【・答え「表面積…9πcm² EF…17/3」】
※cmを省略するものとする。
＊表面積
球の表面積は4πr²で求めることができる。
AB=3なので、半径rは3/2となる。
よって、4×π×(3/2)²=9π(cm²)
＊EF
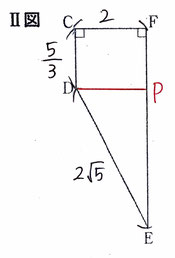
頂点DからEFに向けて垂線を引き、交点をPとすると
EF=EP+PFとなり、三平方の定理から
EP=√(2√5)²-2²=√16=4、
PF=CD=5/3なので、EF=4+5/3=17/3(cm)
問2：
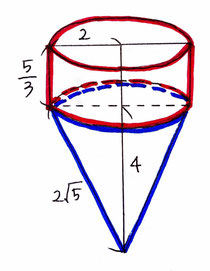
問2：立体Xと立体Yの体積の比を最も簡単な整数の比で表す問題です。
【・答え「3：8」】
※cmを省略するものとする。
(立体X)
球の体積は4/3πr³で求めることができる。
4/3π(3/2)³=9/2π
(立体Y)
立体Yは円柱(赤色で示した部分)と円錐(青色で示した部分)が合体した立体なので、分けて計算する。
円柱の部分=2²×π×5/3=20/3π
円錐の部分=1/3×2²×π×4=16/3π
二つの立体を合わせると、20/3π+16/3π=36/3π=12π
よって、立体X：立体Y=9/2π：12π=3：8となる。
【中期】大問4：二次関数
ブレーキがきき始めてから、自転車が止まるまでに走った距離である制動距離は、速さの2乗に比例することが知られている。太郎さんの乗った自転車が秒速2mで走るときの制動距離は0.5mであるときの各問いに答える問題です。
問1：
問1：自転車が秒速xmで走るときの制動距離をymとしてyをxの式で表す。また、xが5から7まで変化するとき、yの増加量はxの増加量の何倍かを求める問題です。 【・答え「y=1/8x²，1.5倍(または3/2倍)」】
＊xの式
「制動距離は、速さの2乗に比例する」とあるので、
y=ax²に
「秒速2mで走るときの制動距離は0.5m」の数値を代入する。
0.5=a×2² 0.5=4a a=1/2×1/4=1/8
よって、y=1/8x²
＊増加量
x=5のとき、y=1/8×5²=25/8
x=7のとき、y=1/8×7²=49/8となり、
xの増加量は、7-5=2
yの増加量は、49/8-25/8=3
よって、3÷2=3/2 で3/2倍となる。
問2：
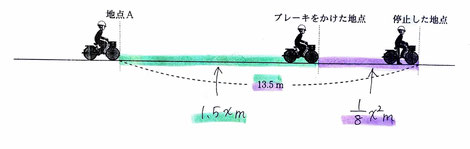
問2：自転車が一定の速さで走っていて、A地点を超えてから1.5秒後にブレーキをかけると自転車がA地点から13.5mのところで停止した。このときの、ブレーキをかける直前の速さを求める問題です。
【・答え「6m/秒」】
ここで求めたい「ブレーキをかける直前の速さ」→x(m)とすると、
緑色で示した、ブレーキをかける前→1.5x(m)
紫色で示した、ブレーキをかけた後→1/8x²(m)
と表すことができる。
それぞれを合わせると13.5(m)となるから、1.5x+1/8x²=13.5
これを計算すると、
与式=12x+x²=108 x²+12x-108=0 (x-6)(x+18)=0
x=6，-18 xは速さなので、x>0
よって、x=6が答え。
【中期】大問5：平面図形
問1：
問1：∠BCGと大きさが等しい角を選択肢(ア)～(カ)の中からすべて選ぶ問題です。
【・答え「ア，オ，カ」】
∠BCGと大きさが等しい角は、図の緑色の二重線で示した部分
∠GCH、∠GBC、∠CAD、∠HDFの4つ。
この4つの中で選択肢にあるのは、ア，オ，カである。
問2：
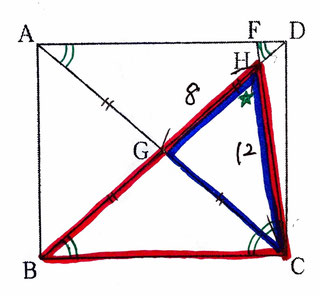
問2：線分BGの長さを求める問題です。
【・答え「10(cm)」】
☆で示した∠Hは共通 …①
問1より、∠GCH=∠CBH …②
①，②より2組の角がそれぞれ等しいので、
△HCG∽△HBC であると言える。
相似な図形の辺の比はそれぞれ等しいので、
12：HB=8：12 8HB：144 HB=18
GH=8なので、18-8=10 よってBG=10(cm)
問3：
問3：△DFHの面積を求める問題です。
【・答え「5√7/12」】
問2より、相似な△HCGと△HBCの相似比は2：3であるから、
2：3=CG：BC 2×BC=3×CG BC=30/2=15
三平方の定理を使って、
DC²=20²-+15²=400-225=175 DC=5√7
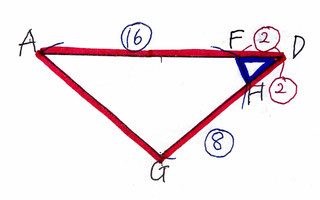
Ⅱ図から△ADGの部分を抜き出すと、画像のようになる。
△ADGの面積：△FDHの面積=18×10：2×2=45：1
△ADGの面積=15×5√7/2×1/2=75√7/4
75√7/4×1/45=15√7/36=5√7/12
【中期】大問6：規則性
問1：
問1：m=4のときの、白い点の個数と黒い点の個数を求める問題です。
【・答え「白…35個 黒…30個」】
問2：
問2：白い点が458個であるmの値と、そのときの黒い点の個数を求める問題です。
【・答え「m=51 黒い点…7550」】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、京都府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
