【奈良県】令和3年度/2021年度入学者高校入試選抜試験：数学の解説
奈良県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
奈良県の数学は4つの大問で構成され、そのうち1つが小問集合となっています。その他の大問は、関数・図形が出てくることが多く空間図形はあまりテーマになることはありません。
難易度は標準といったところです。数学が得意なお子さんであれば満点を狙えると思います。
【奈良県】令和3年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら＞＞
大問1
問題文
次の各問い答えよ。
（1）次の①～④の計算せよ。
① ー2－5
② ー3²×9
③ 8a²b÷(ー2ab)²×6ab
④ (x＋7)(xー4)ー(xー4)²
（2）連立方程式を解け。
{3x+4y=1
{2x-y=-3
（3）2次方程式x²ー3x＋1＝0
（4）√15の小数部分をaとするとき、a²＋6aの値を求めよ。
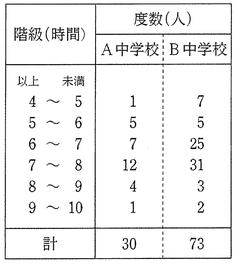
（5）表は、A中学校とB中学校の3年生全生徒を対象に、1日当たりの睡眠時間を調査し、その結果を度数分布表にまとめたものである。この表から読み取ることができることがらとして適切なものを、次のア～エからすべて選び、その記号を書け。
ア 5時間以上6時間未満の階級の相対度数は、A中学校の方が大きい。
イ 睡眠時間が8時間以上の生徒の人数は、A中学校の方が多い。
ウ 睡眠時間の最頻値（モード）は、B中学校の方が大きい。
エ B中学校の半数以上の生徒が、7時間未満の睡眠時間である。
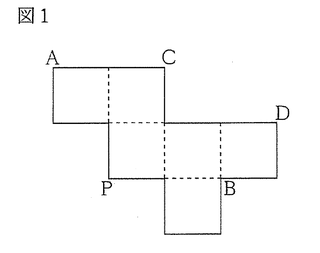
（6）図1は、立方体の展開図である。この展開図を組み立ててできる立体において、頂点Pと頂点A,B,C,Dをそれぞれ結ぶ線分のうち、最も長いものはどれか。次のア～エから1つ選び、その記号を書け。
ア 線分PA
イ 線分PB
ウ 線分PC
エ 線分PD
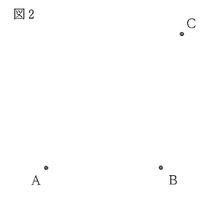
（7）図2のように、3点A,B,Cがある。次の条件①,②を満たす点Pを、定規とコンパスを使って解答欄の枠内に作図せよ。なお、作図に使った線は消さずに残しておくこと。
【条件】
① 点Pは、線分BC上にある。
② ∠BAP＝30°である。
（8）連続する4つの整数のうち、1つの数を除いた3つの整数の和は2021である。①、②の問いに答えよ。
① 連続する4つの整数のうち、最も小さい数をaとするとき、最も大きい数をaを用いて表せ。
② 除いた数を求めよ。
解答・解説
（1）① 【正答 -7】
両方とも負の数なので絶対値の足し算になる
（1）② 【正答 -81】
-3²×9＝-9×9＝-81
（1）③ 【正答 12a】
=(48a³b²)÷4a²b²
（1）④ 【正答 11x-44】
=x²＋3xー28ー(x²ー8x＋16)＝11xー44
（2） 【正答 x=-1, y=1】
3x+4y=1
8x-4y=-12
よりx=-1
-3+4y=1となるので
y=1
（3） 【正答 x=(3±√5)/2】
（4） 【正答 6】
3<√15<4よりa=√15-3
a²+6a=a(a+6)=(√15-3)(√15+3)=15-9=6
（5） 【正答 ア、エ】
ア：Aの相対度数・・・5/30 Bの相対度数・・・5/73（相対度数は小数で表すが、比較のためにここでは分数としている） より正しい
イ：A・・・5人 B・・・5人 より正しくない
ウ：A・・・7.5時間 B・・・7.5時間 より正しくない
エ：Bの7時間未満は37人。37/73より半分を超えるので正しい
（6） 【正答 ウ】
頭の中で展開図を組み立てて実際に長さの比較をするのが適当か。
PA<PB=PC<PD
（7） 【正答】
（8）① 【正答 a+3】
連続する4つの整数とは具体的には1,2,3,4や103,104,105,106とか。
一番小さい数字をaとすれば一番大きい数はa+3であらわされる。
（8）② 【正答 673】
(iv)a+3を除くときを考えると、
(ii)a+1を除くとき
3a=2016
a=672となる。
除いた数はa+1なので673が本問の答え
大問2
問題文
花子さんと太郎さんは、ある博物館で入館料の割引キャンペーンが行われていることを知り、それぞれ何人かのグループで訪れる計画を立てている。次の【 】内は、博物館の入館料と、花子さんと太郎さんのそれぞれの計画をまとめたものである。各問いに答えよ。
（1）次の□内は、グループの入館料の合計金額に関する花子さんと太郎さんの会話である。この会話を読んで、①～③の問いに答えよ。
花子：私のグループの場合、入館料の合計金額は【（あ）】円だね。
太郎：私のグループの場合、月末割引の日に訪れる予定だから、特別割引の日に訪れるよりも入館料の合計金額は【（い）】円高くなるよ。
花子：私のグループが月末割引の日に訪れるとしても、入館料の合計金額は、特別割引の日に訪れるより高くなるよ。
太郎：特別割引の日より、月末割引の日に訪れる方が、グループの入館料の合計金額が安くなることはあるのかな。
花子：大人ｘ人、子どもｙ人のグループで訪れるとして、入館料の合計金額を式に表して考えてみようよ。
① 【（あ）】、【（い）】に当てはまる数を書け。
② 2人は、特別割引について考えている中で、ｘとｙの大小関係により、グループの入館料の合計金額を表す式が異なることに気づいた。ｘ＜ｙであるとき、特別割引の日に訪れる場合のグループの入館料の合計金額をｘ、ｙを用いて表せ。
③ 2人は、グループの入館料の合計金額について、次の【 】内のようにまとめた。【（う）】に当てはまる数を書け。また（X）、（Ｙ）に当てはまる語句の組み合わせを、後のア～エから1つ選び、その記号を書け。
大人の人数より子どもの人数の方が多い場合、2種類の割引でグループの入館料の合計金額が等しくなるのは、子どもの人数が大人の人数の【（う）】倍のときである。このときより、大人の人数が1人（Ｘ）か、子どもの人数が1人（Ｙ）と、特別割引の日より、月末割引の日に訪れる方が、グループの入館料の合計金額が安くなる。
ア Ｘ 増える Ｙ 増える
イ Ｘ 増える Ｙ 減る
ウ Ｘ 減る Ｙ 増える
エ Ｘ 減る Ｙ 減る
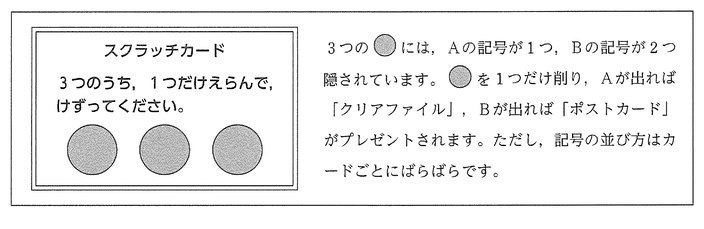
（2）特別割引の日に入館する子どもには、スクラッチカードが配られ、記念品として「クリアファイル」か「ポストカード」のいずれかが必ずプレゼントされる。次の【 】内は、スクラッチカードとその説明である。花子さんのグループの子ども3人のうち、少なくとも1人は「クリアファイル」がプレゼントされる確率を求めよ。
解答・解説
（1）① 【正答 あ:1200 い:200】
あ：大人が二人なので子供二人が無料になる。
500×2+200×1=1200
い：特別割引では500×3+200×2=1900
月末割引では450×3+150×5=2100
差額は200円である
（1）② 【正答 300x+200y】
x<yのとき子供料金はy-x人分であるから
500x+200(y-x)=300x+200y
（1）③ 【正答 3、ウ】
特別割引では300x+200y
月末割引では450x+150y
これらが等しくなるので300x+200y=450x+150y
これを解いて3x=y
x:y=1:3のときに等式が成立。すなわち子供の人数が大人の3倍の時。
また、大人が１人増えると、特別割引では大人が＋500円、子供が－200円、トータルで＋300円。
月末割引では＋450円。
すなわち大人の人数が増えるほど特別割引の方が安くなる。
子供が１人増えると、特別割引では＋200円、月末料金では＋150円。
子供の人数が増えるほど、月末料金の方が安くなる。
（2） 【正答 19/27】
少なくとも一人はAを選ぶという事象は全体から三人ともBを選ぶ事象を除けばよいので
1-2/3×2/3×2/3=19/27
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3
問題文
図のように、関数y＝ax²(a>0)のグラフ上に、2点A,Bがあり、そのｘ座標はそれぞれー1、2である。原点をＯとして、各問いに答えよ。
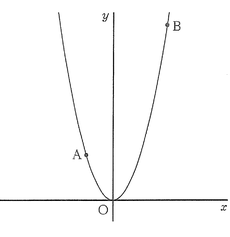
（1）aの値が大きくなると、次の①、②はどのように変化するか。正しいものをそれぞれア～ウから1つずつ選び、その記号を書け。
①グラフの開き方
ア 大きくなる イ 小さくなる ウ 変わらない
②線分ABの長さ
ア 長くなる イ 短くなる ウ 変わらない
（2）xの変域が-1≦x≦2のとき、yの変域が0≦y≦2となる。このときのaの値を求めよ。
（3）a＝2のとき、①,②の問いに答えよ。
①直線ABの式を求めよ。
②線分OA上に点Cをとり、直線BCとy軸との交点をDとする。また、直線ABとy軸との交点をEとする。△BEDの面積と△ODCの面積が等しくなるとき、点Cのx座標を求めよ。
解答・解説
（1）① 【正答 イ】
aの値が大きくなるほどグラフの開きは小さくなる
（1）② 【正答 ア】
グラフの開きが小さくなるほどｘ軸方向は短くなるが、ｙ軸方向は長くなる。
傾きが大きくなるほど長くなる。
（2） 【正答 1/2】
x=2で最大値y=2 (2,2)を通る。
y=ax²に代入してa=1/2
（3）① 【正答 y=2x+4】
y=2x²に代入。A（-1,2）→（2,8）
右に３、上に６だから傾きは２。
Ａから右に１、上に２移動して切片は４。
y=2x+4
（3）② 【正答 -2/3】
Ｃはｙ＝４ｘ＋４とｙ＝－２ｘの交点だから、
４ｘ＋４＝－２ｘ
ｘ＝－２/３
大問4
問題文
図のように、線分ABを直径とする円Oの周上に点Cがあり、AB＝5㎝、AC＝3㎝である。線分AB上に点Dをとり、直線CDと円Oとの交点のうち点C以外の点をEとする。ただし、点は、点A,Bと一致しないものとする。各問いに答えよ。
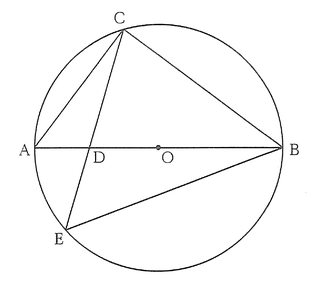
（1）△ACD∽△EBDを証明せよ。
（2）∠BAC＝a°とする。BC＝CEのとき、∠OCDの大きさをaを用いて表せ。
（3）∠AOE＝60°のとき、線分DEの長さは線分ADの長さの何倍か。
（4）AC＝CDのとき、△OEBの面積を求めよ。
解答・解説
（1） 【正答 円周角は等しいので∠ACD=∠EBD
対頂角は等しいので∠ADC=∠EDB
二組の角がそれぞれひとしいので△ACD∽△EBD】
（2） 【正答 90-a】
∠ＣＢＥを∠OＢＥ（=×）と∠OＢC（=●）の二つに分けて考える。
半径よりＯＢ＝ＯＣ、△ＯＢＣは二等辺で∠ＯＣＢ＝●
弧ＡＥに対する円周角より、∠ＡＣＥ＝×
直径に対する円周角より、∠ＡＣＢ＝90°
したがって、∠ＯＣＤ＝90－（●＋×）＝90－ａ°
（3） 【正答 5√3/6】
ＯＢ＝５÷２＝５/２ｃｍ
直角三角形ＯＢＨの辺の比は１：２：√３でＨはＥＢの中点だから、
ＥＢ＝５/２×√３/２×２＝５√３/２ｃｍ
△ＡＣＤ∽△ＥＢＤで、ＡＣ：ＥＢ＝ＡＤ：ＥＤ
＝３：５√３/２＝６：５√３＝１：５√３/６
よって、ＤＥの長さはＡＤの長さの５√３/６倍。
（4） 【正答 42/25】
ＣからＡＢに垂線ＣＨを引くと、△ＣＨＡも３：４：５の直角三角形。
ＣＡ＝⑤とすると、ＡＨ＝③
△ＡＣＤは二等辺三角形で、ＣＨを対称の軸とするとＤＨ＝ＡＨ＝③
ＡＤ＝３×⑥/⑤＝18/５ｃｍ
ＤＢ＝５－18/５＝７/５ｃｍ
ＣＤ：ＡＤ：ＤＢ
＝３：18/５：７/５
＝⑮：⑱：⑦
△ＡＣＤ∽△ＥＢＤより、ＤＥ＝⑱×⑦/⑮＝〇42/５
ＣＤ：ＤＥ＝⑮：〇42/５＝75：42＝25：14
したがって、△ＯＥＢの面積は、６×14/25×１/２＝42/25㎠
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、奈良県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
