【鳥取県】令和4年度/2022年度入学者高校入試選抜試験：数学の解説
鳥取県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の各問いに答えなさい。
問1 次の計算をしなさい。
（1） 8－6÷（－2）
（2） √27－6/√3
（3） （3ｘ+ｙ）/2－（2ｘ-5ｙ）/3
（4） 3ab²×（－4a²）÷6b
問2 ax²－9aを因数分解しなさい。
問3 連立方程式x+y=13、3x-2y=9を解きなさい。
問4 二次方程式2x²-5x+1=0を解きなさい。
問5 一次方程式7x=x+3を、次の【解き方】のように解いた。このとき【解き方】の①の式から②の式へ変形してよい理由として、最も適切なものを、あとのア～エから一つ選び、記号で答えなさい。ただし【ⓐ】には方程式の解が入るが、解を求める必要はない。
【解き方】
7x=x+3
7x-x=3
6x=3 ・・・①
x=【ⓐ】 ・・・②
ア ①の式の両辺から3をひいても等式は成り立つから、②の式へ変形してよい。
イ ①の式の両辺から6をひいても等式は成り立つから、②の式へ変形してよい。
ウ ①の式の両辺を3でわっても等式は成り立つから、②の式へ変形してよい。
エ ①の式の両辺を6でわっても等式は成り立つから、②の式へ変形してよい。
問6 ある動物園の入園料は、おとな1人がa円、子供1人がb円である。このとき、入園料についての不等式「4a+5b≦7000」はどんなことを表しているか、入園料という語句を用いて説明しなさい。
問7 右の図Ⅰにおいて、∠xの大きさを求めなさい。ただし、点Oは円の中心であり、3点Ａ，Ｂ，Ｃは円Ｏの周上の点である。
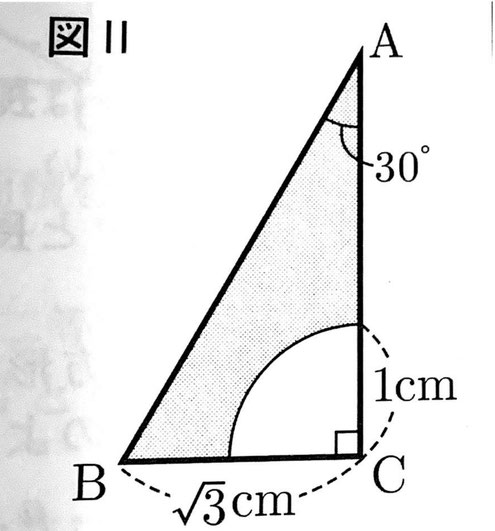
問8 右の図Ⅱのように、BC＝√3ｃｍ、∠Ａ＝30°、∠Ｃ＝90°である直角三角形から、点Ｃを中心とする半径1ｃｍ、中心角90°のおうぎ形を取り除いた図形を、直線ＡＣを回転の軸として1回転させてできる回転体の体積を求めなさい。
問9 一次関数=-3x+5について述べた文として正しいものを、次のア～エから一つ選び、記号で答えなさい。
ア グラフは点（-3，5）を通る直線である。
イ ｘの値が2倍になるとき、ｙの値も2倍になる。
ウ ｘの変域が1≦ｘ≦2のとき、ｙの変域は－1≦ｙ≦2である。
エ ｘの値が1から3まで変わるとき、ｙの増加量は－3である。
問10 大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数をa、小さいさいころの出た目の数をbとする。このとき、√a+bの値が整数となる確率を求めなさい。ただし、さいころは1から6までのどの目が出ることも同様に確からしいとする。
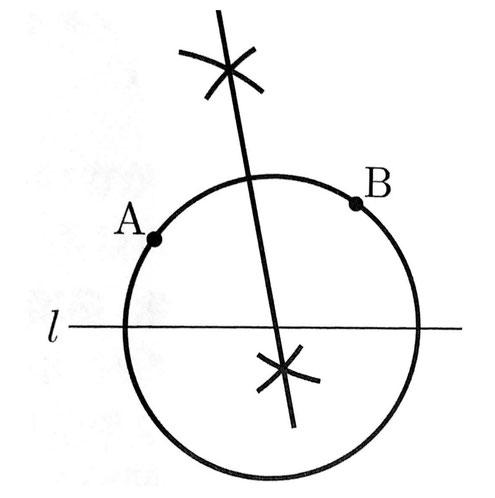
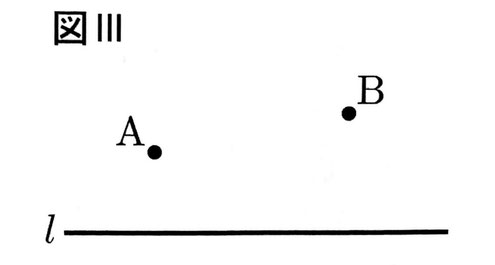
問11 右の図Ⅲにおいて、次の【条件】①、②を満たす円を作図しなさい。ただし、作図に用いた線は明確にして、消さずに残しておくこと。
【条件】
①2点A,Bを通る。
②直線ｌ上に円の中心がある。
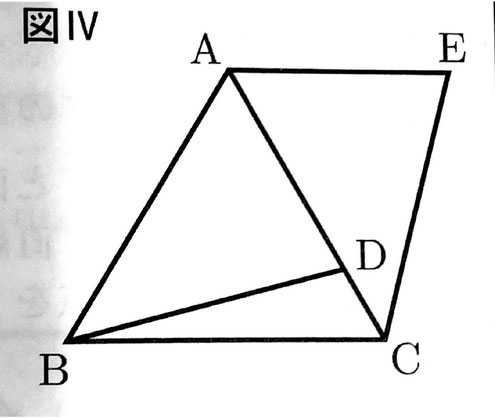
問12 右の図Ⅳのように、正三角形ABCにおいて、辺AC上に点Dをとる。また、点Aを通り辺BCに平行な直線上にAD＝AEとなる点Eをとる。
ただし、∠CAEは鋭角とする。
このとき、△ABD≡△ACEであることを、次のように証明した。あとの（1）～（3）に答えなさい。
【証明】
△ABDと△ACEで、
仮定より、
AD＝AE…①
△ABCは正三角形だから、
AB＝AC…②
∠BAD＝∠ACB＝60°…③
また、【 a 】は等しいから、
∠CAE＝∠ACB＝60°…④
③、④から、
∠BAD＝∠CAE…⑤
①、②、⑤から、【 b 】が、それぞれ等しいので、
△ABD≡△ACE
（1）証明の【 a 】にあてはまるものとして最も適切なものを、次のア～オからひとつ選び、記号で答えなさい。
ア 対頂角 イ 垂線の同位角 ウ 垂線の錯角 エ 平行線の同位角 オ 平行線の錯角
（2）証明の【 b 】にあてはまる最も適切な語句を入れて、証明を完成させなさい。
（3）△ABD≡△ACEを証明したことにより、新たにわかることとして最も適切なものを、次のア～エからひとつ選び、記号で答えなさい。
ア AB＝AC イ BD＝CE ウ ∠BAD＝∠ACB エ ∠BDC＝∠CAE
解答
【解答】
問1（1） 【正答 11】
問1（2） 【正答 √3】
問1（3） 【正答 （5ｘ+13ｙ）/6】
問1（4） 【正答 -2a³b】
問2 【正答 a(x+3)(x-3)】
問3 【正答 x＝7，y＝6】
問4 【正答 x=(5±√17/4)】
問5 【正答 エ】
問6 【正答 （例）おとな4人と子供5人の入園料の合計金額は7000円以下である。】
問7 【正答 28度】
問8 【正答 7/3πｃｍ³】
問9 【正答 ウ】
問10 【正答 7/36】
問11 【正答 右図】
問12（1） 【正答 オ】
問12（2） 【正答 2組の辺とその間の角】
問12（3） 【正答 イ】
【解説】
問1（1） 8-6÷（-2）＝8+3＝11
問1（2） √27-6/√3＝3√3-6/√3×√3/√3＝3√3-2√3＝√3
問1（3） （3ｘ+ｙ）/2-（2ｘ-5ｙ）/3＝3（3ｘ+ｙ）-2（2ｘ+5ｙ）/6＝9ｘ+3ｙ-4ｘ+10ｙ/6＝（5ｘ+13ｙ）/6
問1（4） 3ab²×(-4a²)÷6b=3ab²×（-4a²）/6b＝-2a³b
問2 ax²-9a=a(x²-9)=a(x+3)(x-3)
問3 y=13-xを代入して、3x-2(13-x)=9 3x-26+2x=9 5x=35 x=7 y=13-7=6
問4 2x²-5x+1=0に解の公式を利用する。
問5 ①の式の両辺を6でわっても等式は成り立つから、正しいものはエである。
問7 ∠ｘ+34°＝124°÷2 ∠ｘ＝62°-34°＝28°
問8 求める体積は、円錐の体積から半球の体積を引いて求められるから、
π/3×（√3）²×3-4/3π×1³÷2＝（3-2/3）π＝7/3π（ｃｍ³）
問9
ア：ｘ＝-3のとき、ｙ＝14≠5だから正しくない
イ：ｙはｘに比例しないから正しくない
ウ：ｘ＝1のときｙ＝2、ｘ＝2のときｙ＝-1だから、-1≦ｙ≦2となり正しい
エ：ｘの値が1から3まで2変わるとき、ｙの増加量は-6だから正しくない。
問10 さいころの目の出方は全部で36通りある。このうち、√a+bが整数となるのは、a+bが4または9のときのみで、7通りある。よって、求める確率は7/36である。
問11 線分ABの垂直二等分線と直線ｌとの交点を中心とし、点Aを通る円を描けばよい。
問12（1） ④が成り立つ理由を考えると、平行線の錯角は等しいとなるからオが最も適切である。
問12（2） △ABDと△ACEの合同条件を考えると「2組の辺とその間の角」である。
問12（3）
ア：仮定より、AB＝ACであり、適切でない。
イ：正しく、適切である。
ウ：仮定より、∠BAD＝∠ACBであり、適切でない。
エ：∠BDC＝∠CAEは成り立たないので、適切でない。
大問2
問題文
A～Eの5か所の農園で、それぞれ1日に400個のいちごを収穫した。その中で、A農園とB農園から標本としてそれぞれ35個のいちごを無作為に抽出した。
このとき、次の各問いに答えなさい。
問1 右の表Ⅰは、A農園で抽出した35個のいちごの重さを調べて、度数分布表にまとめたものである。
ただし、【 a 】には整数が入るものとする。
このとき、次の（1）、（2）に答えなさい。
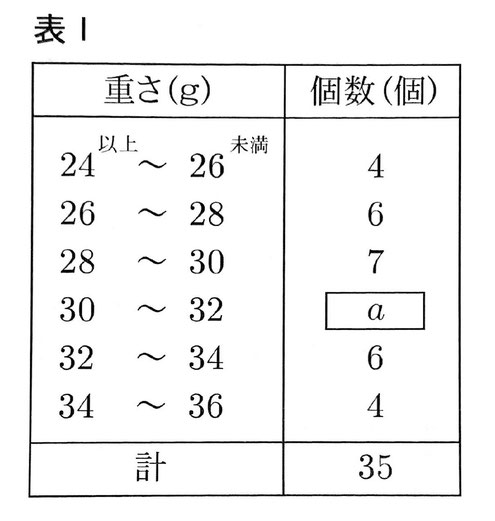
（1）この表Ⅰをもとに、作成したヒストグラムとして、正しいものを次のア～エからひとつ選び、記号で答えなさい。
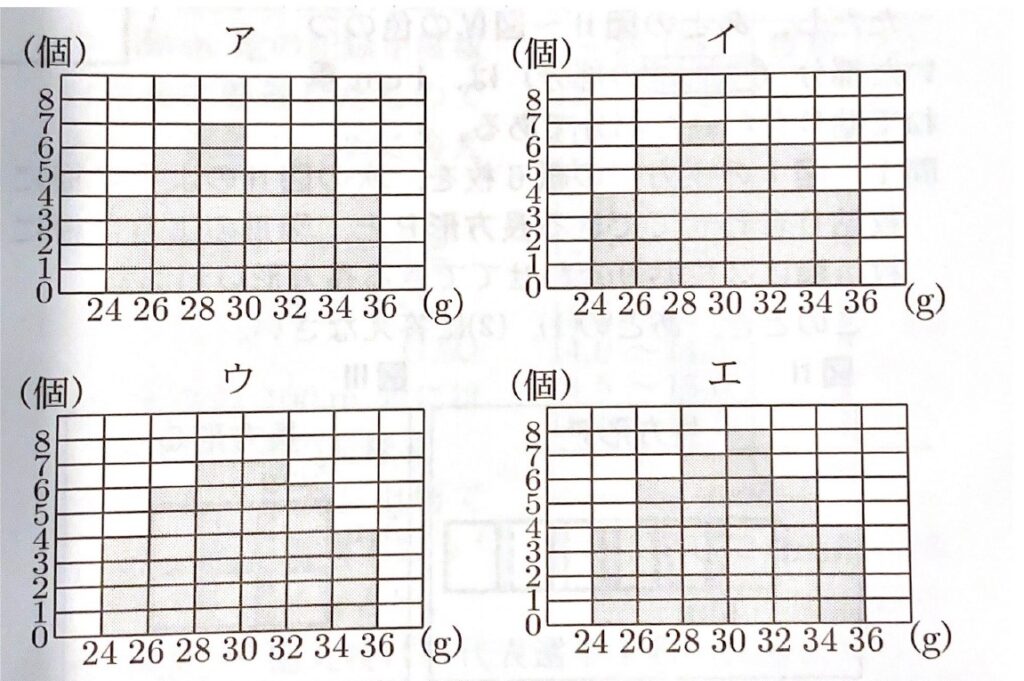
（2）A農園で収穫したいちご400個のうち、重さが28ｇ以上30ｇ未満のいちごが、およそ80個あると推定した。このとき相対度数という語句とその値を用いて、どのように推定したか、説明しなさい。
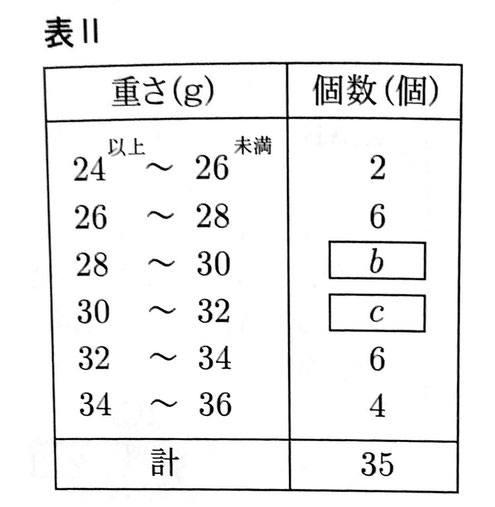
問2 右の表ⅡはB農園で抽出した35個のいちごの重さを調べて。度数分布表にまとめたものである。この度数分布表から最頻値を求めると29ｇであり、中央値は30ｇ以上32ｇ未満の階級に含まれていた。
このとき、表Ⅱの【 b 】【 c 】にあてはまる数をそれぞれ求めなさい。
問3 次の図はC,D,Eの3か所の農園で、それぞれ収穫した400個のいちごの重さを調べて、箱ひげ図にまとめたものである。この箱ひげ図から読み取れることとして正しいものを、あとのア～オから2つ選び、記号で答えなさい。
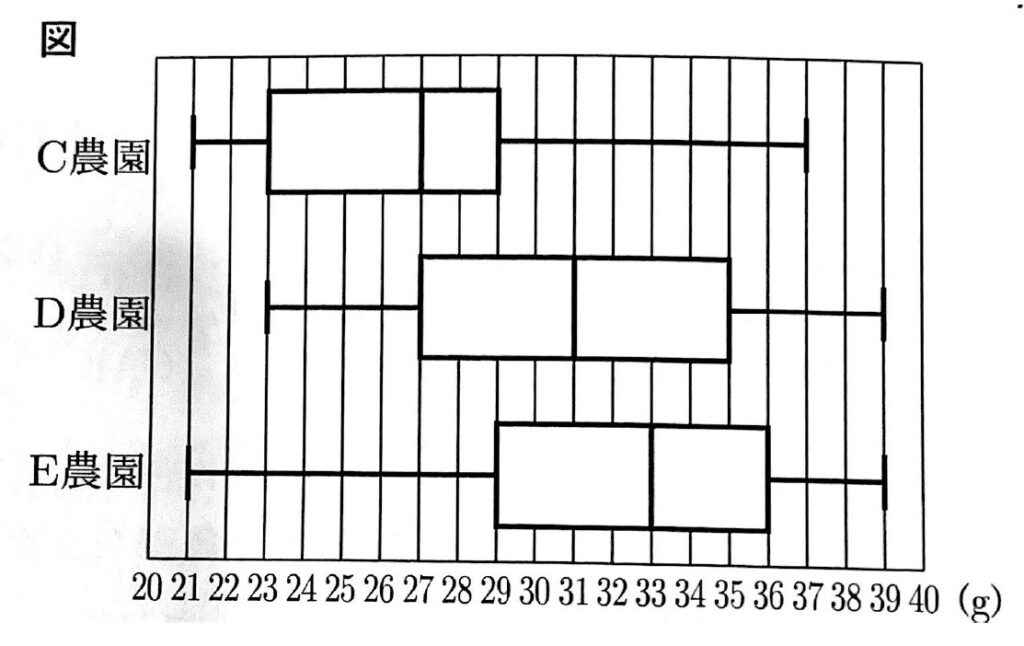
ア C農園のいちごの重さの平均値は27ｇである。
イ C,D,Eの農園の中では、第1四分位数と第3四分位数ともに、E農園が一番大きい。
ウ C,D,Eの農園の中で、重さが34ｇ以上のいちごの個数が一番多いのはE農園である。
エ C,D,Eの農園の中では、四分位範囲は、E農園が一番大きい。
オ 重さが30ｇ以上のいちごの個数は、D農園とE農園ともに、C農園の2倍以上である。
解答
【解答】
問1（1） 【正答 エ】
問1（2） 【正答 （例）母集団の400に相対度数0.2をかけることにより、およそ80個であると推定した。】
問2 【正答 b=9,c=8】
問3 【正答 イ,オ】
【解説】
問1（1） 4+6+7+a+6+4＝35 a＝35-27＝8 よって、エ
問2 2+6+b+c+6+4＝35 b+c＝17
最頻値は29ｇであるからb>cである。
また、中央値は18番目であり、これが30ｇ以上32ｇ未満の階級に含まれているから、c=8 よって、b=9
問3
ア：この箱ひげ図から平均値は読み取れないから正しくない。
イ：正しい。
ウ：重さが34ｇ以上のいちごの個数の比較は、D農園とE農園ではできないから正しくない。
エ：四部位範囲が一番大きいのはD農園だから正しくない。
オ：正しい。
大問3
問題文
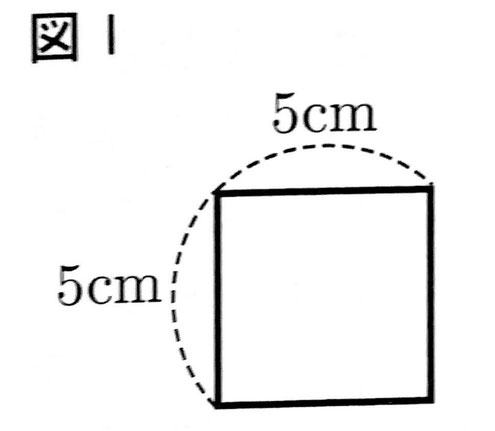
右の図Ⅰのような1辺の長さが5ｃｍである正方形の紙を、1ｃｍ重ねて貼り合わせていく。
このとき、あとの各問いに答えなさい。
ただし、あとの図Ⅱ～Ⅳの色のついた部分は、1ｃｍ重ねて貼り合わせた部分である。
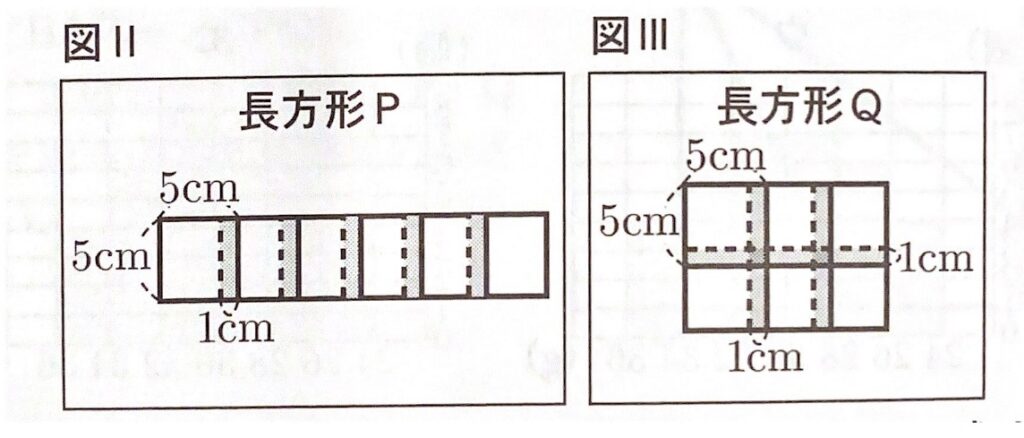
問1 図Ⅰの正方形の紙6枚を、次の図Ⅱのように横に6枚貼り合わせてできる長方形Pと、図Ⅲのように縦に2枚、横に3枚貼り合わせてできる長方形Qである。
このときあとの（1）、（2）に答えなさい。
（1）図Ⅲにおいて、長方形Qの面積を求めなさい。
（2）長方形Pと長方形Qについて述べた文として正しいものを、次のア～オからひとつ選び、記号で答えなさい。
ア 周の長さは長方形Pの方が長く、面積も長方形Pの方が大きい。
イ 周の長さは長方形Pの方が長く、面積は長方形Qの方が大きい。
ウ 周の長さは長方形Qの方が長く、面積は長方形Pの方が大きい。
エ 周の長さは長方形Qの方が長く、面積も長方形Qの方が大きい。
オ 長方形Pと長方形Qでは、周の長さも面積も等しい。
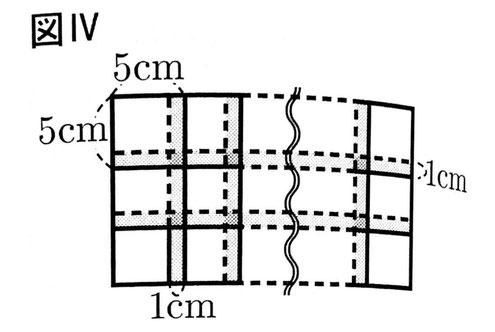
問2 図Ⅰの正方形の紙を、右の図Ⅳのように縦に3枚、横にa枚貼り合わせてできる長方形の面積が377ｃｍ²になった。
このとき、aの値を求めなさい。
ただし、aは自然数とする。
問3 図Ⅰの正方形の紙を、縦にb枚、横にもb枚貼り合わせて出来る正方形の面積が、3600ｃｍ²以下になるように、なるべく大きな正方形を作る。
このときbの値を求めなさい。ただし、bは自然数とする。
解答
【解答】
問1（1） 【正答 117ｃｍ²
問1（2） 【正答 ア】
問2 【正答 a=7】
問3 【正答 b=14】
【解説】
問1（1） 長方形Qの面積は、
（5+4）×（5+4+2）＝9×13＝117（ｃｍ²）
問1（2） 長方形Qの周の長さは、
2×（9+13）＝2×22＝44（ｃｍ）
長方形Pの面積は、5×（5+4×5）＝5×25＝125（ｃｍ²）
長方形Pの周の長さは、2×（5+25）＝60（ｃｍ）
周の長さはPの方が長く、面積もPの方が大きい。
よって、正しいものはアである。
問2 （5+4×2）×｛5+4（a-1）｝＝377 13（4a+1）＝3777 4a+1＝29 a＝7（枚）
問3 ｛5+4（b-1）｝²≦3600 （4ｂ+1）²≦60²
bは自然数だから、4b+1＞0なので、4b+1≦60
b≦59/4＝14.75
よって、最大のbは、b＝14（枚）
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
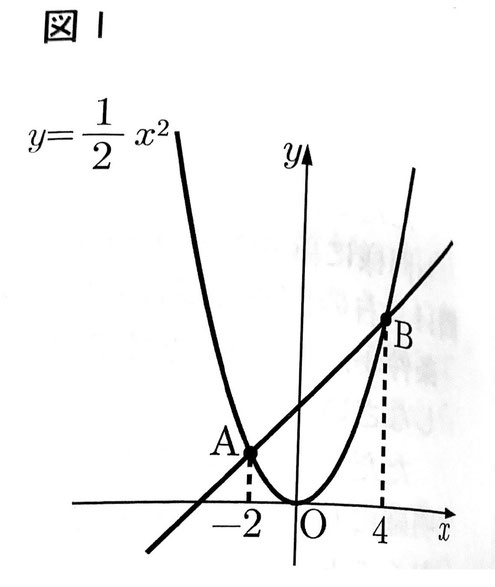
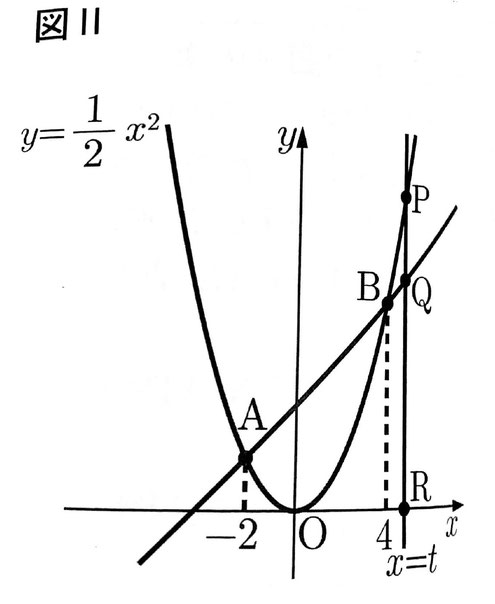
右の図Ⅰのように、関数ｙ＝1/2ｘ²のグラフ上に2点A,Bがある。点A,Bのｘ座標は、それぞれ-2，4である。
このとき、次の各問いに答えなさい。
問1 点Aのｙ座標を求めなさい。
問2 2点A,Bを通る直線の式を求めなさい。
問3 △OABの面積を求めなさい。
問4 右の図Ⅱのように、直線ｘ＝ｔと関数ｙ＝1/2ｘ²のグラフの交点をP、直線ｘ＝ｔと直線ABの交点をQ、直線ｘ＝ｔとｘ軸の交点をRとする。
このとき、次の（1）、（2）に答えなさい。
ただし、ｔ＞4とする。
（1）PQの長さをｔを用いて表しなさい。
（2）PQ：QR＝7：2となるとき、ｔの値を求めなさい。
解答
【解答】
問1 【正答 ｙ＝2】
問2 【正答 ｙ＝ｘ+4】
問3 【正答 12】
問4（1） 【正答 （例）1/2ｔ²-ｔ-4】
問4（2） 【正答 ｔ＝12】
【解説】
問1 ｘ＝-2のとき、ｙ＝2
問2 問1より、A（-2，2） ｘ＝4のとき、ｙ＝8だから、B（4，8）
直線ABの傾きは8-2/4-（-2）＝1だから、直線ABの方程式はｙ＝x+aとおける。
これが点Bを通るから、8=4+a a=4
よって、直線の方程式はｙ＝ｘ+4
問3 △OABの面積は、4×｛4-（-2）｝÷2＝12
問4 （1）ｘ＝ｔのときの、ｙ＝1/2ｘ²、ｙ＝ｘ+4を考えると、
P（ｔ、1/2ｔ²）、Q（ｔ、ｔ+4）だから、
PQ＝1/2ｔ²-（ｔ+4）＝1/2ｔ²-ｔ-4である。
問4 （2）QR＝ｔ+4だから、PQ：QR＝7：2のとき、
2（1/2ｔ²-ｔ-4）＝7（ｔ+4）
ｔ²-2ｔ-8-7ｔ-28＝0
ｔ²-9ｔ-36＝0
（ｔ+3）（ｔ-12）＝0
ｔ＞4より、ｔ＝12
大問5
問題文
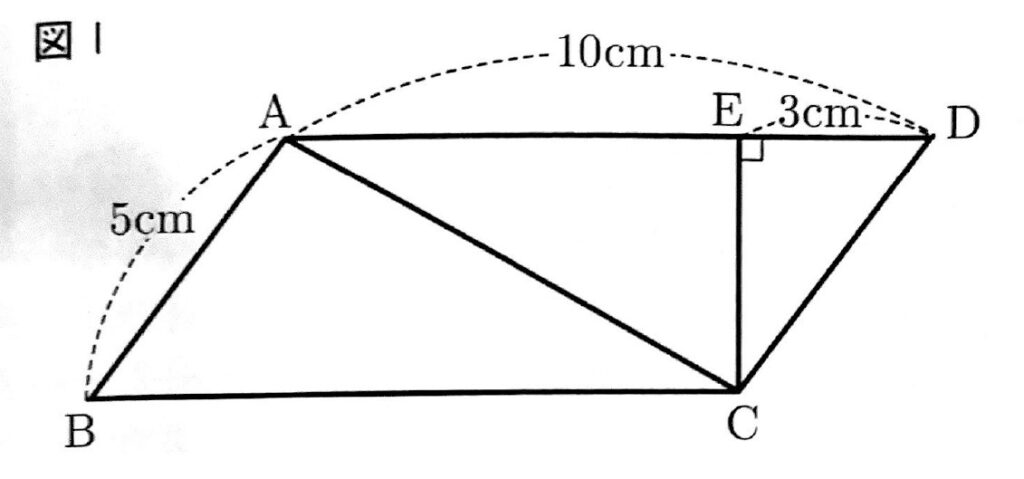
次の図Ⅰのように、AB＝5ｃｍ、AD＝10ｃｍ、∠BADが鈍角の平行四辺形ABCDがある。点Cから辺ADにひいた垂線が辺ADと交わる点をEとし、DE＝3ｃｍである。
このとき、あとの各問いに答えなさい。
問1 △ACEの面積を求めなさい。
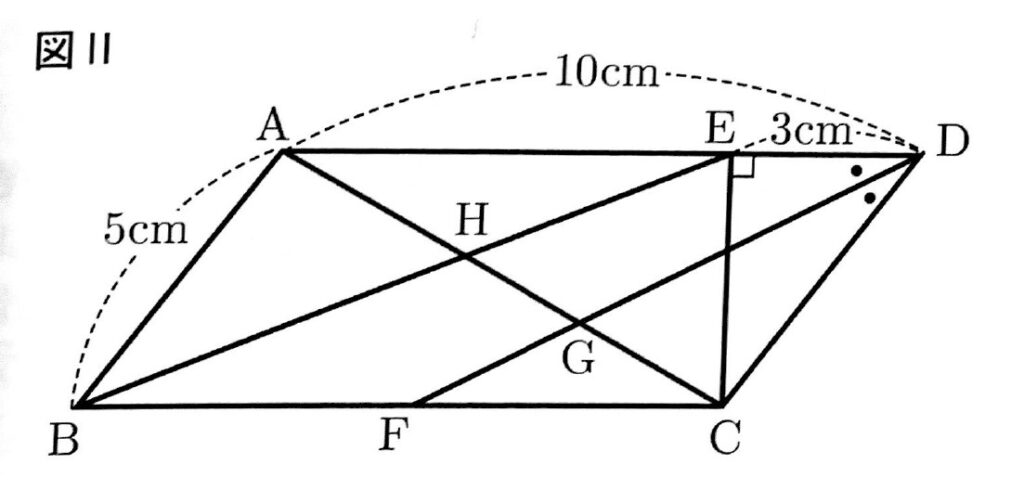
問2 次の図Ⅱのように、∠ADCの二等分線が辺BC、線分ACと交わる点をそれぞれF,Gとする。また、線分ACと線分BEの交点をHとする。
このとき、あとの（1）～（3）に答えなさい。
（1）AH:HCを最も簡単な整数の比で答えなさい。
（2）△CGFの面積を求めなさい。
（3）AH:HG:GCを最も簡単な整数の比で答えなさい。
解答
【解答】
問1 【正答 14ｃｍ²】
問2（1） 【正答 7：10】
問2（2） 【正答 10/3ｃｍ²】
問2（3） 【正答 21：13：17】
【解説】
問1 △CDEで三平方の定理より、CE＝√5²-3²＝4（ｃｍ）
よって、△ACE＝7×4÷2＝14（ｃｍ²）
問2（1） △AHE∽△CHBだから、
AH:CH＝AE:CB＝7：10
問2（2） DGは∠ADCの二等分線だから、AG：GC＝AD：CD＝10：5＝2：1…①
△CGF＝△AGD×（1/2）²＝△ACD×2/3×1/4＝10×4×1/2×2/3×1/4＝10/3（ｃｍ²）
問2（3） （1）、①より、
AH:CH＝7：10＝21：30
AG:GC＝2：1＝34：17
であるから、
AH：HG：GC＝21：（34-21）：17＝21：13：17
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
