






広島県の2022年3月実施の令和4年度(2022年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年度の数学は6つの大問に分かれています。難易度は全体的に標準です。
大問1の小問集合の難易度は易です。全問正解を十分に狙えます。
大問2の難易度は標準~やや難です。(2)の図形問題に気付く力が必要になります。
大問3の関数問題の難易度は標準です。関数と図形が絡む頻出問題です。
大問4の証明問題の難易度は標準です。半円に注目すれば難なくできるかと思います。
大問5の難易度はやや難です。計算自体は大したことがないですが、膨大な文章量の中から必要な情報を取捨選択する技術が必要です。
大問6の難易度は標準です。大問5と同じく文章量が多いですが、<ルール>に従っておけば問題なく答えにたどり着けるはずです。
次の(1)~(8)に答えなさい。
(1)3-24÷(-4)を計算しなさい。
(2)3(4x+y)-5(x-2y)を計算しなさい。
(3)√45-√5+√20を計算しなさい。
(4)x²y-4yを因数分解しなさい。
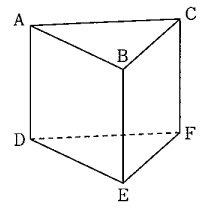
(5)図のように、2つの底面が△ABCと△DEFである三角柱があります。この三角柱において、辺ABとねじれの位置にある辺を全て答えなさい。
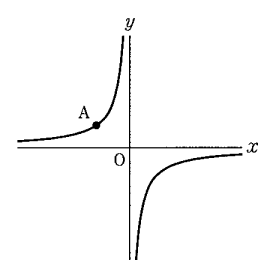
(6)図のように、関数y=a/xのグラフがあります。このグラフが、点A(-3,2)を通るときaの値を求めなさい。
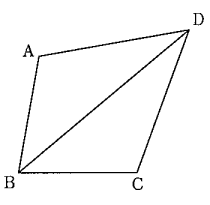
(7)図のように、四角形ABCDがあり、AB=BC、CD=DAです。∠BAD=110°、∠CBD=40°の時、∠ADCの大きさは何度ですか。
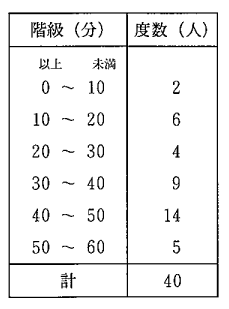
(8)ある学級で、通学時間についてのアンケート調査をしました。右の表は、その結果を度数分布表に整理したものです。
40分以上50分未満の階級の相対度数を求めなさい。
(1) 【正答 9】
加減乗除は乗除から計算する
【与式】=3-(-6)=9
(2) 【正答 7x+13y】
展開して計算すればよい
【与式】=12x+3y-5x+10y=7x+13y
(3) 【正答 4√5】
√は二乗で外に出せる
【与式】=3√5-√5+2√5=4√5
(4) 【正答 y(x+2)(x-2)】
(x²-y²)=(x+y)(x-y)の公式を使えばよい
【与式】=y(x²-4)=y(x+2)(x-y)
(5) 【正答 辺CF,辺DF,辺EF】
ねじれの位置とは交わらず、平行にもならない位置のことをいう。
交わる辺:辺AC,辺BC,辺AD,辺BE
平行な辺:辺DE
を除いたものが答えとなる。
(6) 【正答 -6】
基本式に通る点を代入すればよい
2=a/-3→-6=a
よってa=-6
(7) 【正答 60°】
三辺の長さが等しいので△ABDと△BCDは合同
よって、∠ABD=∠CBD=40°、∠BCD=∠BAD=110°
以上より360°-(40°+110°)×2=60°
(8) 【正答 0.35】
相対度数とは全体に占める割合のことなので
14÷40=0.35
次の(1)~ (3)に答えなさい。
(1)中川さんは、ミルクティーとコーヒー牛乳を作ろうと考えています。ミルクティーは、紅茶と牛乳を2:1の割合で混ぜ、コーヒー牛乳は、コーヒーと牛乳を1:1の割合で混ぜます。
牛乳をちょうど350ml使い、ミルクティーとコーヒー牛乳を同じ量だけ作るとき、紅茶とコーヒーはそれぞれ何ml必要ですか。
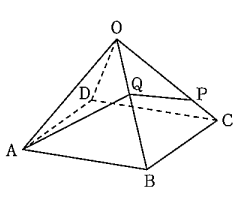
(2)図のように、底面が、1辺の長さが4cmの正方形ABCDで、OA=OB=OC=OD=4cmの正四角すいがあります。辺OC上に、OP=3cmとなるように点Pをとります。辺OB上に点Qをとり、AQ+QPが最小となるようにするとき、AQ+QPは何cmですか。
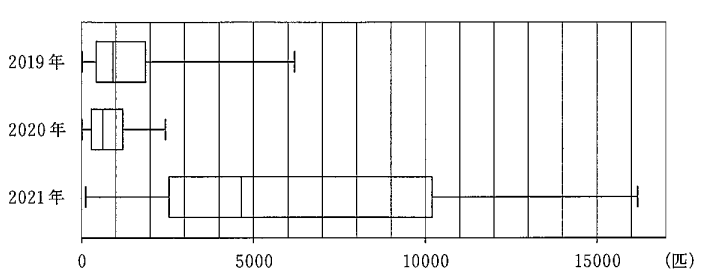
(3)田村さんの住む町では、毎年多くのホタルを見ることができ、6月に最も多く観測されます。そこで田村さんは、6月のホタルの観測数を2019年から2021年までの3年間について調べました。下の図は、それぞれの年の6月の30日間について、日ごとのホタルの観測数を箱ひげ図にあらわしたものです。この箱ひげ図から読み取れることとして正しいものを、下の①~④の中からすべて選び、その番号を書きなさい。
①2019年の6月では、観測されたホタルの数が1000匹未満であった日数が15日以上ある。
②6月に7000匹以上のホタルが観測された日が1日もないのは2020年だけである。
③2021年の6月では、3000匹以上10000匹以下のホタルが観測された日数が15日以上ある。
④4000匹以上のホタルが観測された日数は2021年の6月は2019年の6月の2倍以上ある。
(1) 【正答 紅茶:280、コーヒー:210】
紅茶をxml、コーヒーをymlとすると
ミルクティーとコーヒー牛乳を同じ数だけ作ることから
x+x/2=y+y・・・①
牛乳は合計350ml使うということから
x/2+y=350・・・②
これらを解くと答えを得る。
(2) 【正答 √37
展開し、点AからOCを延長した線と交わる点をRとし、△ARPないし、△AROに注目する。
△AROにおいて、1:2:√3の三角形となるのでAR=2√3、RO=2とわかる。
△ARPにおいて、三平方の定理よりAP²=AR²+RP²=37となる。
AQ+QP=APなので、答えは√37
(3) 【正答 ①、④】
②:7000匹以上のホタルは2021年のみ観測されているので2020年だけではなく、不適。
③:箱(全体の50%)のうち、3000以上10000以下は箱より小さい範囲にあるので15日以上ないため、不適。
下の図のように、関数y=1/4x²のグラフがあります。また、方程式y=-3のグラフ上をx>0の範囲で動く点A、x<0の範囲で動く点Bがあります。点Aを通りy軸に平行な直線と、関数y=1/4x²のグラフとの交点をC、点Bを通りy軸に平行な直線と、関数y=1/4x²のグラフとの交点をDとします。
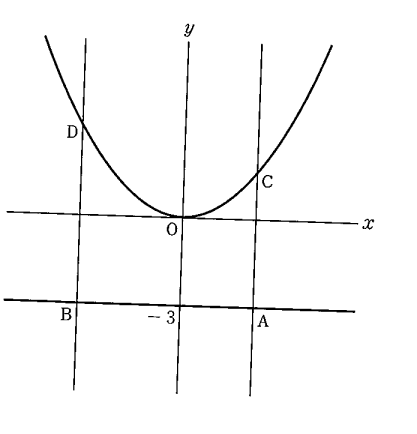
次の(1)・(2)に答えなさい。
(1)点Aのx座標が4、△OBAの面積が9となるとき、点Bのx座標を求めなさい。
(2)四角形DBACが正方形となるような点Aのx座標を全て求めなさい。
(1)【正答 -2】
点Aの座標は(4,-3)となる。点Bのx座標をxbとすると、△OBAの面積が9となることから
(4+(-xb))×3÷2=9
よって、xb=-2
(2)【正答 2,6】
A,Bのy座標は常にy=-3であるから、正方形となるためには、C,Dのy座標も等しくなる。
C,Dのy座標をy’、A,Bのx座標をx’、-x’とすると、y’=1/4x’²となる。
正方形はすべての辺の長さが等しくなるので
x’-(-x’)=1/4x’²-(-3)
よって、x’=2,6
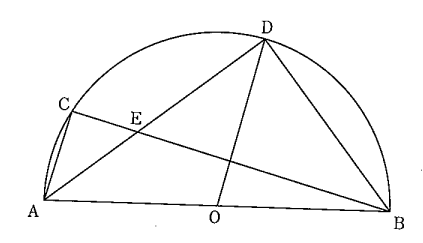
下の図のように、線分ABを直径とする半円があり、点Oは線分ABの中点です。弧AB上に、AとBとは異なる点Cをとります。弧BC上にAC//ODとなるような点Dをとり、線分BCと線分ADの交点をEとします。このとき、△AEC∽△ABDであることを証明しなさい。
【正答
△AECと△ABDにおいて
半円の弧に対する円周角なので
∠ACE=∠ADB・・・①
平行線の錯角となるので
∠CAE=∠ADO・・・②
OA=ODなので、△AODは二等辺三角形であり
∠ADO=∠DAB・・・③
②、③より、∠CAE=∠DAB・・・④
①、④より、二組の角がそれぞれ等しいので
△AEC∽△ABD】
A社の中村さんと山下さんはP市の港から12km離れたQ島の港へのドローン(無人航空機)を使った宅配サービスを始めたいと考えています。そこで、A社の所有するドローンが、宅配サービスに使用できるかについて話をしています。
中村「この宅配サービスでは、最大5kgの荷物を運ぶことにしたいんだ。私たち、A社のドローンは、バッテリーを100%に充電した状態で5kgの荷物を載せてP市を出発し、Q島へ届けた後、再充電することなくP市に戻ってこられるかな。」
山下「バッテリー残量が30%以下になると、安全に飛行することが難しくなるよ。だから、宅配サービスに使用するためには、往復してもバッテリー残量が30%以下にならないことを確かめないといけないね。」
中村「そうだね。それでは、荷物を載せない場合と、5kgの荷物を載せる場合のそれぞれで、ドローンの飛行時間に伴うバッテリー残量の変化について調べてみようよ。」
2人は、荷物を載せない場合と、5kgの荷物を載せる場合のそれぞれについて、A社のドローンのバッテリーを100%に充電して、常に分速1.2kmで飛行させ、1分ごとにバッテリー残量を調べました。そして、ドローンが飛び始めてから、x分後のバッテリー残量をy%として、その結果をそれぞれ次のように表1,表2にまとめ、下の図1,図2にあらわしました。
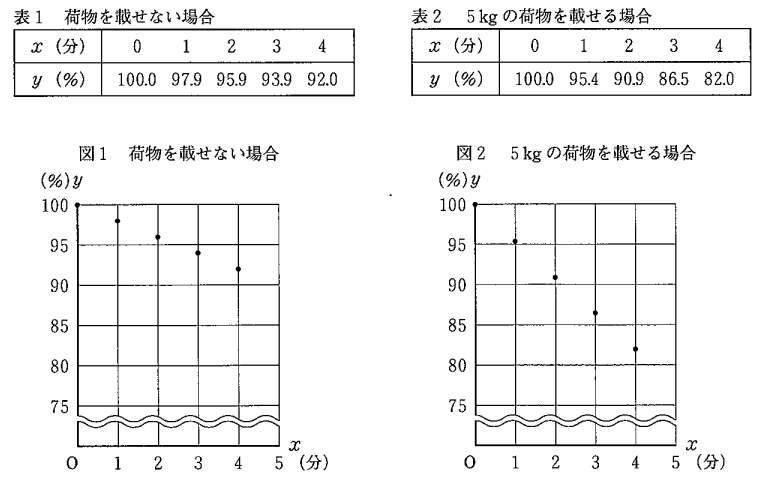
中村さんたちは表1,表2と図1,図2をもとに、A社のドローンが宅配サービスに使用できるかを考えました。
中村「図1,図2を見ると、いずれの場合も5つの点がほぼ一直線上に並んでいるから、どちらもyはxの一次関数とみなして考えてみようよ。」
山下「それでは、荷物を載せない場合は、グラフが①2点(0,100)、(4,92)を通る直線となる一次関数と考え、5kgの荷物を載せる場合は、グラフが2点(0,100)、(4,82)を通る直線となる一次関数としよう。
中村「この2つの一次関数をもとに、②5kgの荷物をQ島に届けてP市に戻ってくるまでのドローンの飛行時間とバッテリー残量の関係を表すグラフをかくと、A社のドローンが宅配サービスに使用できるか分かると思うよ。」
山下「では、グラフをかいて考えてみよう。」
次の(1)・(2)に答えなさい。
(1)下線部①について、荷物を載せない場合において、yをxの式で表しなさい。
(2)下線部②について、バッテリーを100%に充電したA社のドローンが、5kgの荷物を載せ、P市の港を出発してQ島の港で荷物を降ろし、荷物を載せない状態でP市の港に戻ってくるまでの飛行時間とバッテリー残量の関係を表すグラフを書きなさい。また、グラフをもとにA社のドローンがこの宅配サービスに使用できるか、使用できないかを、その理由とともに説明しなさい。ただし、ドローンの上昇・下降にかかる時間とそれに伴うバッテリー消費、およびQ島の港で荷物を降ろす際にかかる時間は考えないものとします。
(1) 【正答 y=-2x+100】
一次関数になるので基本式y=ax+bに代入し
100=b・・・①
92=4a+b・・・②
の2式を得る、ここから、y=-2x+100となる。
(2) 【正答 グラフは略解。
往復で20分かかるが、20分後のバッテリー残量は35%である。バッテリー残量が30%以下にならないため、A社のドローンは宅配サービスに利用できる。】
PからQまで12kmを分速1.2kmで行くので10分かかる。表2から(4,82)(0,100)を通るので直線はy=-9/2x+100となり、(10,55)を通る。
荷物を降ろした後は表1の直線なので(1)と同じ傾きになるので(20,35)を通る。
太郎さんと次郎さんは、次の【ゲーム】において、先にカードを取り出す人と、後からカードを取り出す人とでは、どちらが勝ちやすいかを調べることにしました。
【ゲーム】
図のように、1,2,3,4の数字が一つずつ書かれた4枚のカードが入った袋があります。下の図のように、正方形ABCDの頂点Aにコマを置きます。このコマを太郎さんと次郎さんの2人が下の<ルール>に従って、正方形ABCDの頂点から頂点へ移動させ、勝敗を決めます。
<ルール>
①先に、太郎さんが袋の中のカードをよく混ぜ、そこから1枚取り出し、カードに書かれた数字の数だけ、正方形の頂点から頂点へ反時計回りにコマを移動させる。
②太郎さんは、取り出したカードを袋に戻し、次郎さんに交代する。
③次に、次郎さんが袋の中のカードをよく混ぜ、そこから1枚取り出し、①で移動させたコマが置いてある頂点から、カードに書かれた数字の数だけ、正方形の頂点から頂点へ反時計回りにコマを移動させる。
④それぞれが移動させた後のコマの位置によって、下の表のⅠ~Ⅳのように勝敗を決めることとする。

例えば、太郎さんが2の数字が書かれたカードを取り出したとき、太郎さんはコマをA→B→Cと移動させます。次に次郎さんが1の数字が書かれたカードを取り出したとき、次郎さんはコマをC→Dと移動させます。この場合は、太郎さんが移動させた後のコマは頂点Cにあり、次郎さんが移動させた後のコマは頂点Dにあるので、Ⅳとなり引き分けとなります。
次の(1)・(2)に答えなさい。
(1)この【ゲーム】において、太郎さんが移動させた後のコマの位置が、頂点Bである確率を求めなさい。
2人は、太郎さんが勝つ確率と、次郎さんが勝つ確率をそれぞれ求めました。その結果から、この【ゲーム】では、先にカードを取り出す人と、後からカードを取り出す人とでは、勝ちやすさに違いがないことが分かりました。
(2)さらに【ゲーム】の中の<ルール>の②だけを、②’にかえた新しいゲームでも、カードを取り出す順番によって勝ちやすさに違いがないかを調べることにしました。
②’太郎さんは、取り出したカードを袋に戻さず、次郎さんに交代する。
この新しいゲームにおいて、先にカードを取り出す人と、後からカードを取り出す人とでは、勝ちやすさに違いはありますか。下のア~ウの中から正しいものを1つ選び、その記号を書きなさい。また、それが正しいことの理由を、確率を用いて説明しなさい。
ア:先にカードを取り出す人と後からカードを取り出す人とでは、勝ちやすさに違いはない。
イ:先にカードを取り出す人が勝ちやすい。
ウ:後からカードを取り出す人が勝ちやすい。
(1) 【正答 1/4】
Bに来るのは1のカードを引くときのみなので、1/4
(2) 【正答 ウ
先にカードを取り出す太郎さんが勝つ確率は1/6であり、後からカードを取り出す次郎さんが勝つ確率は1/4である。後からカードを取り出す人が勝つ確率が大きいので、後者が有利となる。】
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています!
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…?」とご質問いただくことも多いですが、ご安心ください!家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです!
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

