【香川県】令和4年度/2022年度入学者高校入試選抜試験：数学
香川県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の⑴～⑺の問いに答えなさい。
（1）3×(-5)+9 を計算せよ。
（2）5(x-2y)-(4x+y) を計算せよ。
（3）(6a²-4ab)÷2a を計算せよ。
（4）(√8+1)(√2-1) を計算せよ。
（5）3x²-12 を因数分解せよ。
（6）2次方程式 (x-2)²=5 を解け。
（7）次のア～エのうち、nがどのような整数であっても、連続する2つの奇数を表すものはどれか。正しいものを1つ選んで、その記号を書け。
ア n,n+1
イ n+1,n+3
ウ 2n,2n+2
エ 2n+1,2n+3
解答
【解答】
（1） 【正答 -6】
（2） 【正答 x-11y】
（3） 【正答 3a-2b】
（4） 【正答 3-√2】
（5） 【正答 3(x+2)(x-2)】
（6） 【正答 x=2±√5】
（7） 【正答 エ】
【解説】
（1） （与式）＝-15+9＝-6
（2） （与式）＝5ｘ-10ｙ-4ｘ-ｙ＝ｘ-11ｙ
（4） （与式）＝√16-√8+√2-1＝4-2√2+√2-1＝3-√2
（5） （与式）＝3（ｘ²-4）＝3（ｘ+4）（ｘ-4）
（6） ｘ-2＝±√5 ｘ＝2±√5
大問2
問題文
次の⑴～⑶の問いに答えなさい。
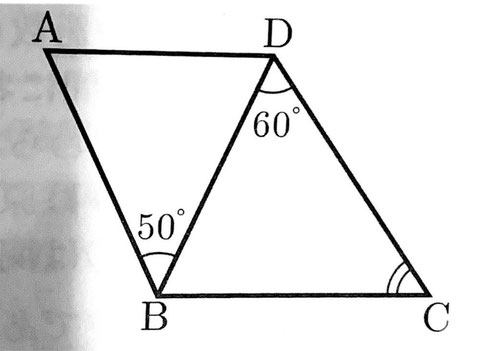
（1）図のようなAD//BCの台形ABCDがあり、AB＝BDである。∠ABD＝50°、∠BDC＝60°であるとき、∠BCDの大きさは何度か。
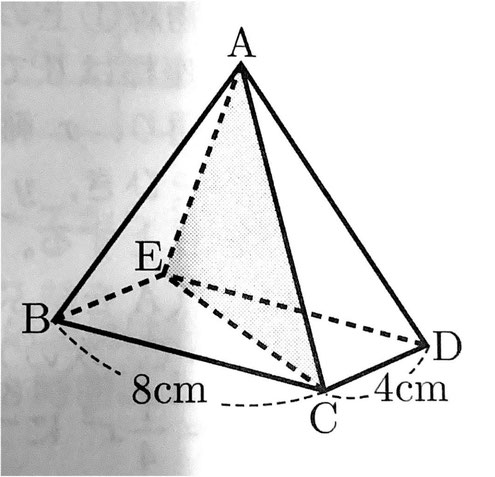
（2）図のような四角錐があり、底面は長方形で、4辺AB,AC,AD,AEの長さはすべて等しい。点Cと点Eを結ぶ。
BC＝8ｃｍ、CD＝4ｃｍ、△ACEの面積が30ｃｍ²であるとき、次のア、イの問いに答えよ。
ア 次のア～エの辺のうち、面ABCと平行な辺はどれか。正しいものを1つ選んで、その記号を書け。
ア 辺BE
イ 辺DE
ウ 辺AD
エ 辺AE
イ この四角錐の体積は何ｃｍ³か。
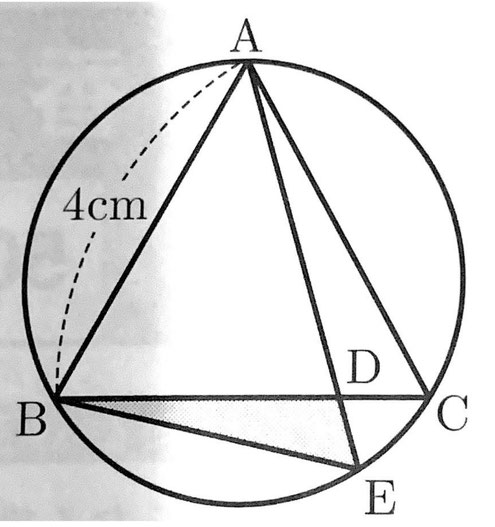
（3）図のような円があり、異なる3点A,B,Cは円周上の点で、△ABCは正三角形である。辺BC上に、2点B,Cと異なる点Dをとり、2点A,Dを通る直線と円との交点のうち、点Aと異なる点をEとする。また、点Bと点Eを結ぶ。
AB＝4ｃｍ、BD：DC＝3：1であるとき、△BDEの面積は何ｃｍ²か。
解答
【解答】
（1） 【正答 55度】
（2） 【正答 ア. イ イ. 32√5㎝³】
（3） 【正答 9√3/13㎝²】
【解説】
（1）
AB＝BDより、∠ADB＝（180°-50°）÷2＝65°
AD//BCより、∠DBC＝∠ADB＝65°
∠BCD＝180°-65°-60°＝55°
（2）イ
EC＝√8²+4²＝√80＝4√5
Aから底面BCDEに垂線AHを下ろすとき、HはECの中点と一致する。
△ACE＝4√5×AH×1/2＝30
AH＝30×2/4√5＝3√5
四角錐の体積は、8×4×3√5×1/3＝32√5（cm³）
（3）
AからBCに垂線AHを下ろす。△ABHは30°、60°、90°の直角三角形であるから、
BH＝2、AH＝2√3、HD＝DC＝1、AD＝√（2√3）²+1²＝√13
△BDE∽△ADCを利用する。
△BDE：△ADC＝BD²：AD²＝3²：（√13）²＝9：13
△BDE＝9/13△ADC＝9/13×（1×2√3×1/2）＝9√3/13（㎝²）
大問3
問題文
次の⑴～⑷の問いに答えなさい。
（1）1から6までのどの目が出ることも、同様に確からしいさいころが1個ある。このさいころを2回投げて、1回目に出た目の数をa、2回目に出た目の数をbとするとき、10a+bの値が8の倍数になる確率を求めよ。
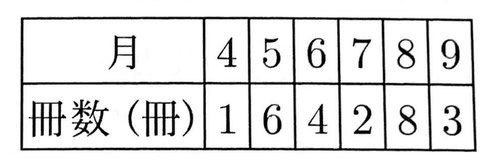
（2）右の表は、4月から9月までの6か月間に、太郎さんが図書館で借りた本の冊数を月ごとに記録したものである。太郎さんは、10月に4冊の本を図書館で借りたので、10月の記録をこの表に付け加える前後の代表値について述べようとしたものである。文中の2つの[ ]内にあてはまる言葉を、ア～ウから一つ、エ～カから1つ、それぞれ選んでその記号を書け。
太郎さんが図書館で借りた本の冊数について、4月から9月までの6か月間における月ごとの冊数の平均値に比べて、4月から10月までの7か月間における月ごとの冊数の平均値は、[ア：大きい イ：変わらない ウ：小さい]。また、4月から9月までの6か月間における月ごとの冊数の中央値に比べて、4月から10月までの7カ月間における月ごとの冊数の中央値は、[エ：大きい オ：変わらない カ：小さい]。
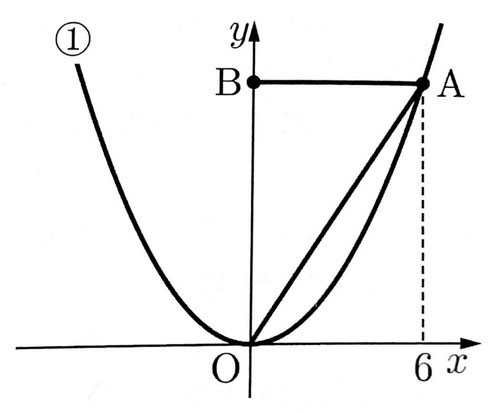
（3）右の図で、点Oは原点であり、放物線①は関数y=1/4x²のグラフである。点Aは放物線①上の点で、そのx座標は6である。点Aを通り、x軸に平行な直線をひき、y軸との交点をBとする。また、点Oと点Aを結ぶ。これについて、次のア、イの問いに答えよ。
ア 関数y=1/4x²について、xの値が-3から-1まで増加するときの変化の割合を求めよ。
イ x軸上に、x座標が負の数である点Pをとり、点Pと点Bを結ぶ。∠OAB＝∠BPOであるとき、直線APの式を求めよ。
（4）ある店で売られているクッキーの詰め合わせには、箱A、箱B、箱Cの3種類があり、それぞれ決まった枚数のクッキーが入っている。箱Cに入っているクッキーの枚数は、箱Aに入っているクッキーの枚数の2倍で、箱A、箱B、箱Cに入っているクッキーの枚数は27枚である。花子さんが、箱A、箱B、箱Cをそれぞれ8箱、4箱、3箱買ったところ、クッキーの枚数の合計は118枚であった。このとき、箱A、箱Bに入っているクッキーの枚数をそれぞれa枚、b枚として、a,bの値を求めよ。a,bの値を求める過程も、式と計算を含めて書け。
解答
【解答】
（1） 【正答 5/36】
（2） 【正答 イとエ】
（3） 【正答 ア. -1 イ. y=3/4x+9/2】
（4） 【正答 下記参照】
（求める過程）
［例］箱Cに入っているクッキーの枚数＝2a（枚）
a+b+2a=27 3a+b=27…①
8a+4b+3×2a=118 14a+4b=118…②
①、②を連立して解くと、a=5,b=12
（答）aの値5,bの値12
【解説】
（1） 10a+bの値が8の倍数になるのは、16，24，32，56，64の5通り。
（2）
4月から9月までの6ヶ月間における月ごとの冊数の平均値は、1+6+4+2+8+3/6=4（冊）
4月から10月までの平均値も、1+6+4+2+8+3+4/7=4（冊）となり、変わらない。
4月から9月までの6か月間における月ごとの冊数の中央値は、3+4/2=3.5（冊）
4月から10月までの中央値は4であるから、大きくなる。
（3）ア
1/4×(-1)²-1/4×(-3)²/-1-(-3)=-2/2=-1
（3）イ
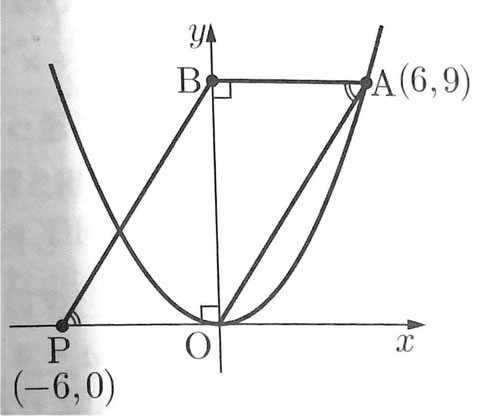
次の図のように、∠OAB＝∠BPOより、△OAB≡△BPOがいえるので、OP＝AB＝6、P（-6，0）A（6，9）を通るので、直線APの式は、y=3/4x+9/2となる。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
次の⑴，⑵の問いに答えなさい。
（1）次の図1のような立方体や正四面体があり、次のルールに従って、これらの立体に・印をつける。
【ルール】
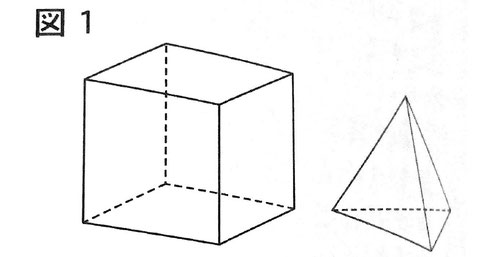
① 最初に、2以上の自然数を1つ決め、それをnとする。
② ①で決めたnの値に対して、図1のような立方体と正四面体に、次のように・印をつける。
立方体については、
各辺をn等分するすべての点とすべての頂点に・印をつける。
正四面体については、
各辺をn等分するすべての点とすべての頂点に・印をつける。また、この正四面体の各辺の中点に・印がつけられていない場合には、この正四面体の各辺の中点にも・印をつける。
③ ②のようにして、立方体につけた・印の個数をa個、正四面体につけた・印の個数をb個とする。
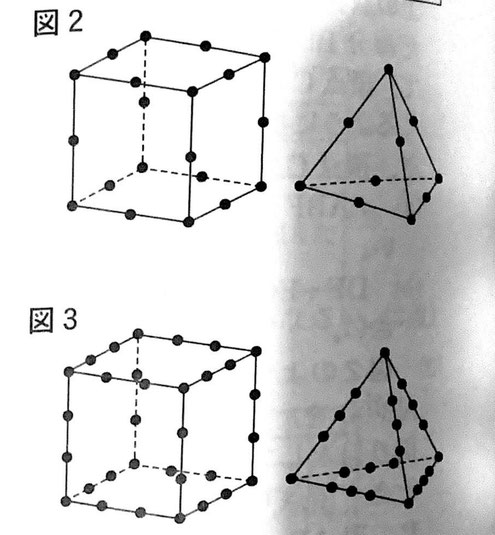
たとえば、最初に、nを2に決めて・印をつけたとき、・印をつけた立方体と正四面体は次の図2のようになり、a=20,b=10である。
また、最初に、nを3に決めて・印をつけたとき、・印をつけた立方体と正四面体は次の図3のようになり、a=32,b=22である。
これについて、次のア、イの問いに答えよ。
ア 最初に、nを5に決めて・印をつけたときの、aの値を求めよ。
イ 2以上の自然数nの値に対して、ルールにしたがって・印をつけたとき、a-b=70となった。このようになるnの値をすべて求めよ。
（2）次の図1のように、BC＝6cm、CD＝8cmの長方形ABCDと、FG=6cm、GH=4cmの長方形EFGHがある。点Aと点Eは重なっており、点Fは辺ABをAの方に延長した直線状にある。
図1の状態から、長方形ABCDを固定して、点Eが対角線AC上にあるようにして、矢印の向きに長方形EFGHを平行移動させる。次の図2は、移動の途中の状態を示したものである。
点Eが、点Aを出発して、毎秒1cmの速さで、対角線AC上を点Cに重なるまでに動くとき、点Eが点Aを出発してからx秒後に、長方形ABCDと長方形EFGHが重なってできる図形をSとして、あとのア～ウの問いに答えよ。
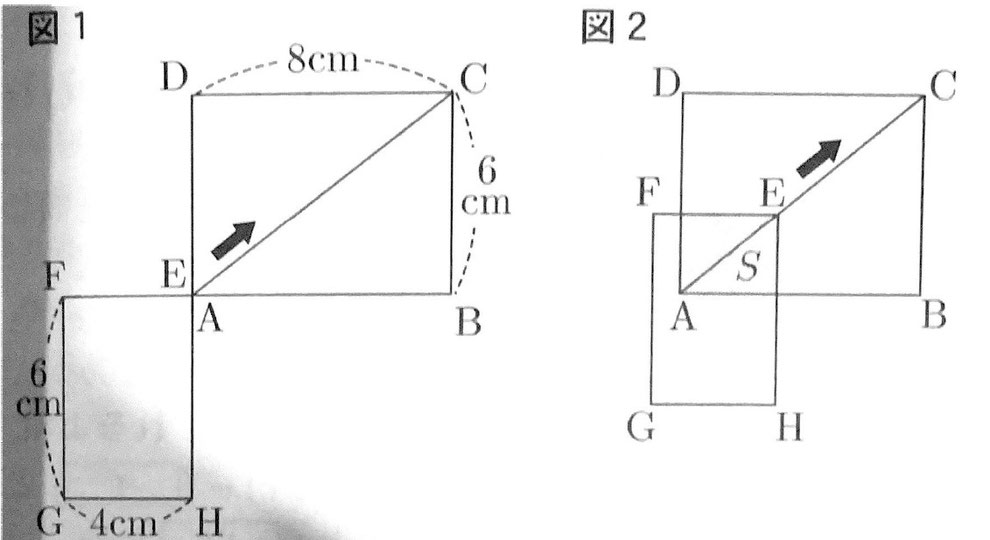
ア 点Fが辺DA上にあるとき、図形Sの面積は何cm²か。
イ 0≦x≦5、5≦x≦10のそれぞれの場合について、図形Sの面積は何cm²か。xを使った式で表せ。
ウ 点Eが点Aを出発してからt秒後にできる図形Sの面積に比べて、その6秒後にできる図形Sの面積が5倍になるのは、tの値がいくらのときか。tの値を求める過程も、式と計算を含めて書け。
解答
【解答】
（1） 【正答 ア. a=56 イ. 12,13】
（2） 【正答 ア. 12cm² イ. [0≦x≦5]12/25x²cm² [5≦x≦10]12/5xcm² ウ. 下記参照】
ウ（求める過程）
[例]t≧0およびt+6≦10より、0≦t≦4
前問イの結果より、t秒後、(t+6)秒後の図形Sの面積はそれぞれ12/25t²、12/5(t+6)と表せる。
5×12/25t²=12/5(t+6)
整理すると、t²-t-6=0 (t+2)(t-3)=0 t=-2,3
0≦t≦4より、t=3
（答）tの値 3
【解説】
（1）ア
立方体につけた・印の個数は、nが1増えるごとに、立方体の辺の本数12ずつ増える。
n=3のとき、a=32であるから、n=5のとき、a=32+12×2=56
（1）イ
アを踏まえて、aの値はnの一次式で表せる。
(n,a)=(2,20),(3,32)を用いると、a=12n-4
正四面体につけた・印の個数は、各辺につける・印が1個増えるごとに、正四面体の辺の本数6ずつ増える。
nが奇数のときには、各辺の中点にも・印をつけるので、表にして整理すつと下表のようになる。
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | 20 | 32 | 44 | 56 | 68 | 80 | 92 | 104 | 116 | 128 | 140 | 152 | 164 |
| b | 10 | 22 | 22 | 34 | 34 | 46 | 46 | 58 | 58 | 70 | 70 | 82 | 82 |
| a-b | 10 | 10 | 22 | 22 | 34 | 34 | 46 | 46 | 58 | 58 | 70 | 70 | 82 |
a-b=70となるのは、n=12,13のときである。
方程式を用いて解く場合、bをnで表す際にnが奇数のときと偶数のときを考える必要がある。
[ｎが偶数の時]
b=10+6(n-2)=6n-2
a-b=12n-4-(6n-2)=6n-2
6n-2=70を解くと、n=12
[ｎが奇数の時]
b=10+6(n-2)+6=6n+4
a-b=12n-4-(6n+4)=6n-8
6n-8=70を解くと、n=13
（2）ア
S＝3×4＝12（cm²）
（2）イ
[0≦x≦5]
S＝3/5x×4/5x=12/25x²
[5≦x≦10]
S=3/5x×4＝12/5ｘ
大問5
問題文
次の図のような、線分ABを直径とする半円Oがあり、弧AB上に2点A,Bと異なる点Cをとる。∠BACの二等分線をひき、半円Oとの交点のうち、点Aと異なる点をDとする。線分ADと線分BCとの交点をEとする。また、点Cと点Dを結ぶ。
このとき、次の（1）（2）の問いに答えなさい。
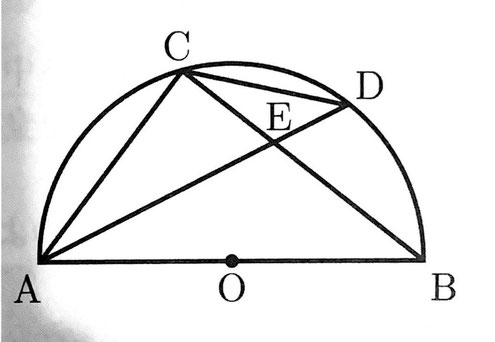
（1）△ACD∽△AEBであることを証明せよ。
（2）点Dから線分ABに垂線をひき、その交点をFとする。線分DFと線分BCとの交点をGとする。点Oと点Dを結び、線分ODと線分BCとの交点をHとする。点Oと点Gを結ぶとき、△OFG≡△OHGであることを証明せよ。
解答
【解答】
（1）証明
[例] △ACDと△AEBにおいて、
仮定より、∠CAD＝∠EAB…①
弧ACに対する円周角は等しいので、∠ADC＝∠ABC
∠ABC＝∠ABEであるから、∠ADC＝∠ABE…②
①、②より、2組の角がそれぞれ等しいので、
△ACD∽△AEB
（2）証明
[例]半径が等しいので、OA＝OD＝OB…①
①より、△OADは二等辺三角形であるから、
∠OAD＝∠ODA、∠CAD＝∠OAD[仮定]より、∠CAD＝∠ODA
錯覚が等しいので、AC//OD…②
△ODFと△OBHにおいて
∠DOF＝∠BOH[共通]…③
半円の弧に対する円周角より、∠ACB＝90°
②より同位角が等しいので、∠OHB＝∠ACB＝90°
∠OFD＝90°[仮定]より、∠OFD＝∠OHB＝90°…④
①、③、④より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、△ODF≡△OBH
対応する辺の長さは等しいので、OF＝OH…⑤
△OFGと△OHGにおいて、
OGは共通…⑥
④より、∠OFG＝∠OHG＝90°…⑦
⑤、⑥、⑦より、直角三角形の斜辺と他の1辺がそれぞれ等しいので、△OFG≡△OHG
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
