【香川県】令和3年度/2021年度入学者高校入試選抜試験：数学
香川県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の⑴～⑺の問いに答えなさい。
（1）2ー(-5)ー4 を計算せよ。
（2）3÷1/4×(-2²) を計算せよ。
（3）等式 3(4xーy)=6 をyについて解け。
（4）√12－9/√3 を計算せよ。
（5）xy－6x＋y－6 を因数分解せよ。
（6）2次方程式 x²＋5x＋2＝0 を解け。
（7）次のア～ウの数の絶対値が，小さい順に左から右に並ぶように，記号ア～ウを用いて書け。
ア －3
イ 0
ウ 2
解答
（1） 【正答 3】
（2） 【正答 －48】
（3） 【正答 ｙ＝4x－2】
（4） 【正答 －√3】
（5） 【正答 （ｘ＋1)(ｙ－6）
（6） 【正答 -5±√17/2】
（7） 【正答 イ→ウ→ア】
大問2
問題文
次の⑴～⑶の問いに答えなさい。
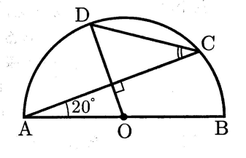
（1）次の図のような，線分ABを直径とする半円Oがある。
Ａ⌒Ｂ上に2点A，Bと異なる点Cをとる。また，点Ｏを通り，線分ACに垂直な直線をひき，半円Ｏとの交点をＤとする。
∠OCA＝20° であるとき，∠ACD の大きさは何度か。
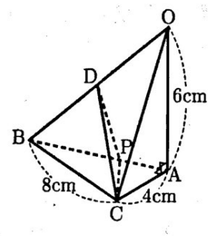
（2）次の図のような，∠OAB＝∠OAC＝∠BAC＝90° の三角すいOABCがある。辺OBの中点をDとし，辺AB上に2点A，Bと異なる点Pをとる。点Cと点D，点Dと点P，点Pと点Cをそれぞれ結ぶ。
OA＝6㎝，AC＝4㎝，BC＝8㎝であるとき，次にア，イの問いに答えよ。
【ア】次のア～エのうち，この三角すいに関して正しく述べたものはどれか。1つ選んで，その記号を書け。
㋐ ∠OCA＝60°である
㋑ 面OABと面OACは垂直である
㋒ 辺OCと面ABCは垂直である
㋓ 辺OAと線分CDはは平行である
【イ】三角すいDBCPの体積が，三角すいOABCの体積の1/3倍であるとき、線分BPの長さは何㎝か。
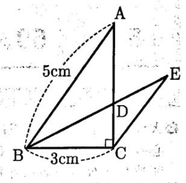
（3）次の図のような，∠ABC＝90°の直角三角形ABCがある。∠ABCの二等分線をひき，辺ACとの交点をDとする。また，点Cを通り，辺ABに平行な直線をひき，直線BDとの交点をEとする。
AB＝5㎝，BC＝3㎝であるとき、線分BEの長さは何㎝か。
解答
（1） 【正答 35度】
（2） 【正答 ア. ㋑ イ. 8√3/3㎝】
（3） 【正答 12√5/5㎝】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3
問題文
次の⑴～⑷の問いに答えなさい。
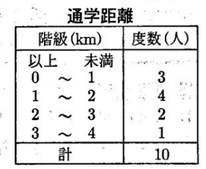
（1）次の表は，ある学級の生徒10人について，通学距離を調べて，度数分布表に整理したものである。この表から，この10人の通学距離の平均値を求めると何kmになるか。
（2）数字を書いた5枚のカード1⃣，1⃣，2⃣，3⃣，4⃣がある。この5枚のカードをよくきって，その中から，もとにもどさず続けて2枚を取り出し，はじめに取り出したカードに書いてある数を a，次に取り出したカードに書いてある数を b とする。このとき，a ≧ b になる確率を求めよ。
（3）次の図で，点Oは原点であり，放物線①は関数 y＝－1/3x² のグラフである。放物線②は関数 y＝ax² のグラフで，a > 0 である。
2点A，Bは，放物線②上の点で，点Aのｘ座標は-3であり，線分ABはｘ軸に平行である。また，点Aを通り，ｙ軸に平行な直線をひき，放物線①との交点をCとし，直線BCをひく。
これについて，次のア，イと問いに答えよ。
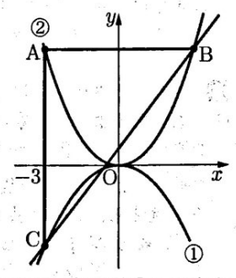
ア 関数 y＝－1/3x²で，ｘの変域が －1≦ｘ≦2 のとき，ｙの変域を求めよ。
イ 直線BCの傾きが5/4であるとき，a の値を求めよ。
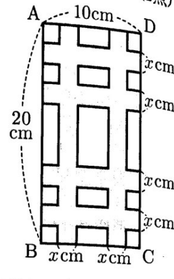
（4）次の図のように，AB＝20㎝，AD＝10㎝ の長方形ABCDの紙に，幅がｘ㎝のテープを，辺ABに平行に2本，辺ADに平行に4本はりつけた。図中の色のある部分■は，テープがはられている部分を示している。テープがはられていない部分すべての面積の和が，長方形ABCDの面積の36％であるとき，ｘの値はいくらか。ｘの値を求める過程も，式と計算を含めて書け。
解答
（1） 【正答 1.6km】
（2） 【正答 11/20】
（3） 【正答 ア. -4/3 ≦ｙ≦ 0 イ. a ＝1/2】
（4） 【正答 ｘの値 2】
（ｘの値を求める過程）
［例］テープがはられていない部分の面積の和は
(10－2x)(20－4x)㎠と表せる。
(10－2x)(20－4x)＝10×20×36/100
8x²－80x＋200＝72
ｘ²－10x＋16＝0
(ｘ－2)(ｘ－8)＝0
ｘ＝2，8
0 < x < 5 より，ｘ＝2
（答）ｘの値 2
大問4
問題文
次の⑴，⑵の問いに答えなさい。
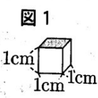
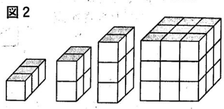
（1）次の図1のような，1面だけ黒く塗られた，1辺の長さが1㎝の立方体がたくさんある。この立方体を，黒く塗られた面をすべて上にして、すきまなく組み合わせ，いろいろな形の四角柱をつくる。たとえば，図2の四角柱は，図1の立方体をそれぞれ3個，4個，6個，27個組み合わせたものである。
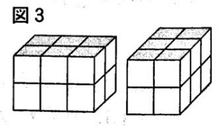
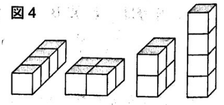
このとき，高さが等しく，上の面の黒い長方形が合同な四角柱は，同じ形の四角柱だとみなす。たとえば，右の図3の2つの四角柱は，高さが2㎝で等しく，上の面の黒い長方形が合同であるから，同じ形の四角柱だとみなす。したがって，図1の立方体を4個組み合わせた四角柱をつくるとき，右の図4のように，異なる形の四角柱は全部で4通りできる。
下の表は，図1の立方体をｎ個組み合わせた四角柱をつくるとき，異なる形の四角柱が全部でｍ通りできるとして，ｎとｍの値をまとめようとしたものである。
これについて，次のア，イの問いに答えよ。
ア 表中のｐの値を求めよ。
イ ｍ＝4 となるｎのうち，2けたの数を1つ求めよ。
（2）太郎さんと次郎さんは，次のルールにしたがって，ゲームをおこなった。これについて，あとのア～ウの問いに答えよ。
【ルール】
太郎さんと次郎さんのどちらか1人が，表と裏の出方が同時に確からしい硬貨を3枚同時に投げる。この1回のゲームで，表と裏の出方に応じて，次のように得る点数を決める
3枚とも表が出れば，
太郎さんの得る点数は4点，次郎さんの得る点数は0点
2枚は表で1枚は裏が出れば，
太郎さんの得る点数は2点，次郎さんの得る点数は1点
1枚は表で2枚は裏が出れば，
次郎さんの得る点数は2点，太郎さんの得る点数は1点
3枚とも裏が出れば，
次郎さんの得る点数は4点，太郎さんの得る点数は0点
ア 太郎さんが3回，次郎さんが3回硬貨を投げて6回のゲームをおこなったとき，1枚は表で2枚は裏が出た回数は3回であり，3枚とも表が出た回数，2枚は表で1枚は裏が出た回数，3枚とも裏が出た回数はともに1回ずつであった.。このとき，太郎さんが得た点数の合計は何点か。
イ 太郎さんが5回，次郎さんが5回硬貨を投げて10回のゲームをおこなったとき，2枚は表で1枚は裏が出た回数は1回であった。このとき，次郎さんが得た点数の合計は何点か。10回のゲームのうち，3枚とも表がでた回数を a 回，3枚とも裏が出た回数を b 回として，次郎さんが得た点数の合計を a と b を使った式で表せ。
ウ 太郎さんが5回，次郎さんが5回硬貨を投げて10回のゲームをおこなったとき，2枚は表で1枚は裏が出た回数は1回であった。また，この10回のゲームで，表が出た枚数の合計は12枚であって，次郎さんが得た点数の合計は太郎さんが得た点数の合計より，7点大きかった。このとき，10回のゲームのうち，3枚とも表が出た回数と3枚とも裏が出た回数はそれぞれ何回か。3枚とも表がでた回数を a 回，3枚とも裏が出た回数を b 回として，a, b の値を求めよ。a, b の値を求める過程も，式と計算を含めて書け。
解答
（1） 【正答 ア. ｐ＝5 イ. 25, 49（から1つ）】
（2） 【正答 ア. 9点 イ. （-2a＋2b＋19）点 ウ. aの値 2， bの値 3】
ウ（a, bの値を求める過程）
[例]1枚は表で2枚は裏が出る回数は（9－a－b）回と表せるので，10回のゲームで表が出た枚数の合計について方程式を立てると，
3a＋2×1＋1×（9－a－b）＝12
整理すると，2a－b＝1…①
太郎さんが得た点数の合計は，
4a＋2×1＋1×（9－a－b）＝3a－b＋11点
と表せるので，前問イの結果を用いると，
-2a＋2b＋19－（3a－b＋11）＝7
整理すると，5a－3b＝1…②
①，②を連立して解くと，a ＝ 2，b ＝ 3
（答）aの値 2， bの値 3
大問5
問題文
次の図のような，正方形ABCDがあり，辺AD上に，2点A，Dと異なる点Eをとる。∠BCEの二等分線をひき，辺ABとの交点をFとする。辺ABをBの方に延長した直線上にDE＝BGとなる点Gをとり，線分GEと線分CFとの交点をHとする。点Eを通り，辺ABに平行な直線をひき，線分CFとの交点をIとする。
このとき，次の⑴，⑵の問いに答えなさい。
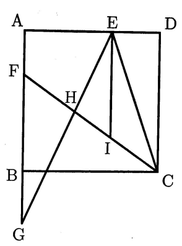
（1）△FGH ∽ △IEH であることを証明せよ。
（2）CE＝FG であることを証明せよ。
解答
（1）証明
[例] △FGHと△IEHにおいて，
∠FHG＝∠IHG（対頂角）
FG∥EIより，∠GFH＝∠EIH（平行線の錯角）
2組の角がそれぞれ等しいので，△FGH ∽ △IEH
（2）証明
[例] 2点のC，Gを結ぶ。
△CDEと△CBGにおいて，
DE=BG（仮定）
四角形ABCDは正方形であるから，
CD＝CB，∠CDE＝90°，
∠CBG＝180°－∠ABC＝180°－90°＝90°
∠CDE＝∠CBG
2組の辺とその間の角がそれぞれ等しいので，
△CDE＝△CBG…（＊）
（＊）より，CE＝CG…①，∠DCE＝∠BCG…②
線分CFは∠BCEを2等分するので，
∠ECF＝∠BCF…③
∠DCF＝∠DCE＋∠ECF，∠GCF＝∠BCG＋∠BCF
②，③より，∠DCF＝∠GCF…④
DC∥FGより，錯角は等しいので，∠DCF＝∠GFC…⑤
④，⑤より，∠GCF＝∠GFC…⑥
⑥より，CG＝FG…⑦
①，⑦より，CE＝FG
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
