【愛媛県】令和4年度/2022年度入学者高校入試選抜試験：数学
愛媛県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の計算をして、答えを書きなさい。
１ -3-6
２ (2x-5y)/3+(x+3y)/2
３ (3x²y-2xy²)÷xy
４ √10/√2-(√5-2)²
５ (a-3)(a+3)+(a+4)(a+6)
解答
【解答】
１ 【正答 -9】
２ 【正答 (7x-y)/6】
３ 【正答 3x-2y】
４ 【正答 5√5-9】
５ 【正答 2a²+10a+15】
【解説】
２ （与式）={2(2x-5y)+3(x+3y)}/6=(4x-10y+3x+9y)/6=(7x-y)/6
３ （与式）=3x²y/xy-2xy²/xy=3x-2y
４ （与式）=√5-(5-4√5+4)=5√5-9
５ （与式）=a²-9+a²+10a+24=2a²+10a+15
大問2
問題文
次の問いに答えなさい。
１ 二次方程式5x²+4x-1=0を解け。
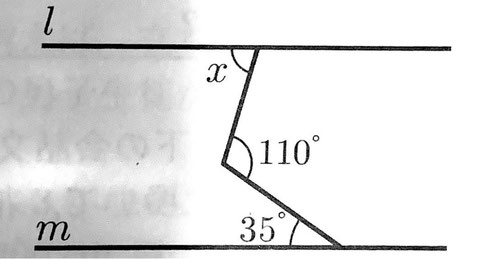
２ 次の図で、l//mのときの、∠xの大きさを求めよ。
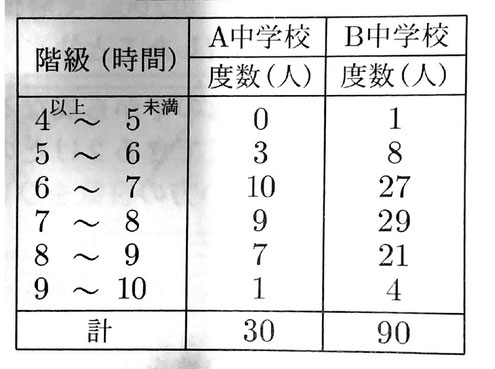
３ 次の表は、A中学校の1年生30人とB中学校の1年生90人について、ある日の睡眠時間を調べ、その結果を度数分布表に整理したものである。この表から分かることを述べた文として正しいものを、次のア～エから1つ選び、その記号を書け。
ア A中学校とB中学校で、最頻値は等しい。
イ A中学校とB中学校で、8時間以上9時間未満の階級の相対度数は等しい。
ウ A中学校で、7時間未満の生徒の割合は、40％以下である。
エ B中学校で、中央値が含まれる階級は、6時間以上7時間未満である。
４ 袋の中に赤玉4個と白玉2個の合計6個の玉が入っている。この袋の中から同時に2個の玉を取り出すとき、赤玉と白玉が1個ずつである確率を求めよ。ただし、どの玉が取り出されることも同様に確からしいものとする。
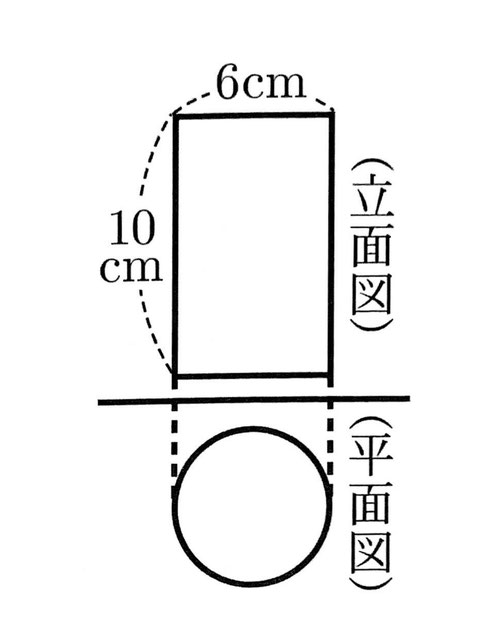
５ 次の図は、円柱の投影図である。この円柱の体積を求めよ。（円周率はπを用いること。）
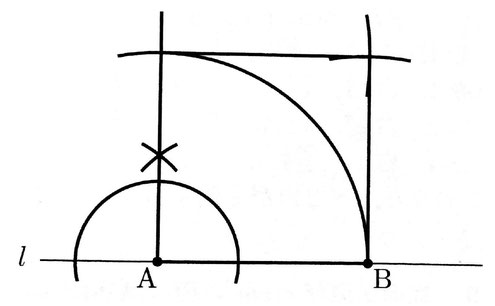
６ 次の図のように、直線l上に2点A,Bがある。線分ABを1辺とする正方形のうち、A,B以外の頂点が、直線lより上側にあるものを作図せよ。ただし、作図に用いた線は消さずに残しておくこと。
７ 次の資料は、ある中学校が発行した図書館便りの一部である。この図書館便りを読んで、9月に図書館を利用した男子と女子の人数を、それぞれ求めよ。ただし、用いる文字が何を表すかを最初に書いてから連立方程式をつくり、答えを求める過程も書くこと。
解答
【解答】
１ 【正答 x=1/5,-1】
２ 【正答 75度】
３ 【正答 イ】
４ 【正答 8/15】
５ 【正答 90πcm³】
６ 【正答 図を参照】
７ 【正答 下記参照】
【解説】
１ 解の公式を用いればよい。
２ ∠x+35°＝110°より、∠ｘ＝75°
３
ア A,Bの最頻値はそれぞれ、6.5（時間）、7.5（時間）なので正しくない。
イ A,Bの8時間以上9時間未満の相対度数はそれぞれA：7/30、B：21/90＝7/30より、正しい。
ウ Aの7時間未満の生徒の割合は(10+3)/30≒0.43より、正しくない。
エ Bの中央値が含まれる階級は下から45番目と46番目を含む階級だから、7時間以上8時間未満の階級であるため、正しくない。
４ すべての起こりうる場合は15通り。そのうち、赤と白が1個ずつの場合は8通りあるので、8/15
５ 底面が直径6ｃｍの円、高さが10ｃｍの円柱であるから、3²π×10＝90π（cm³）
７
9月に図書館を利用した男子をｘ人、女子をｙ人とすると、
x+y=253-33…①
21/100x+10/1000y=33…②
②から、21x+10y=3300…③
③-①×10よりｘ＝100
ｘ＝100を①に代入して、ｙ＝120
（答）9月に図書館を利用した男子、女子の人数はそれぞれ100人、120人
大問3
問題文
次の会話文は、太郎さんが、数学の授業で学習したことについて、花子さんと話をしたときのものである。
【数学の授業で学習したこと】
太郎さん：選んだ2つの数が3，5のとき、大きい方の整数は53，小さい方の整数は35だから、P＝53-35＝18となり、確かにPは9の倍数だね。
花子さん：それなら、3けたの時はどうなるのかな。1～9の自然数の中から異なる3つの数を選び、この3つの数を並べて出来る3けたの整数のうち、最も大きい整数から最も小さい整数をひいた値をQとして考えてみようよ。
太郎さん：例えば、選んだ3つの数が1，3，4のとき、並べてできる3けたの整数は、134，143，314，341，413，431だね。最も大きい整数は431，最も小さい整数は134だから、Q＝431-134＝297となるね。
花子さん：選んだ3つの数が2，6，7のとき、Qは【ア】となるね。
太郎さん：Qも何かの倍数になるのかな。授業と同じように、文字式を使って考えてみようよ。
花子さん：選んだ3つの数をa,b,c(a>b>c)とすると、最も大きい整数は100a+10b+c、最も小さい整数は【イ】と表されるよね。するとQ＝（100a+10b+c）-（【イ】）となって、これを計算すると、【ウ】×(a-c)となるね。a-cは整数だから、Qは【ウ】の倍数となることが分かるよ。
このとき、次の問いに答えなさい。
１ 会話文中のアに当てはまる数を書け。
２ 会話文中のイに当てはまる式、ウに当てはまる数をそれぞれ書け。
３ 1～9の自然数の中から異なる3つの数の選び、Qについて考えるとき、
（1）Q＝396となるときの、3つの数の選び方は全部で何通りあるか。
（2）選んだ3つの数の中に、3と8の、2つの数が含まれるときのQの値を全て求めよ。
解答
【解答】
１ 【正答 ア 495】
２ 【正答 イ 100c+10b+a ウ 99】
３ 【正答 （1）15通り （2）495，594，693】
【解答】
１ このとき並べてできる3けたの数のうち最も大きいものは762、最も小さいものは267であるから762-267＝495
２ウ Q＝（100a+10b+c）-(100c+10b+a)＝99a-99c＝99（a-c）
３（1） Q＝396となるとき、99（a-c）＝396よって、a-c＝4、したがって（a>b>c）に注意してa-c＝4となる場合を考えればよい。
３（2） 条件を満たす３つの数の選び方は（a,b,c）=（9,8,3）（8,7,3）（8,6,3）（8,5,3）（8,4,3）（8,3,2）（8,3,1）の7通り。このうちQ＝99（a-c）であることを考えると、(a,c)=(9,3)(8,3)(8,1)だけ考えればよいので、Q＝495，594，693
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
次の図1のように、AB=10cm,BC=acmの長方形ABCDと、∠P＝90°,PQ=PR=bcmの直角二等辺三角形PQRがある。長方形ABCDの辺ABと直角二等辺三角形PQRの辺PQは直線l上にあり、点Aと点Qは同じ位置にある。
この状態から、次の図2のように、直角二等辺三角形PQRを直線lにそって、矢印の向きに、点Qが点Bに重なるまで移動させる。AQ＝xcmのときの、2つの図形が重なっている部分の面積をycm²とする。
このとき、次の問いに答えなさい。
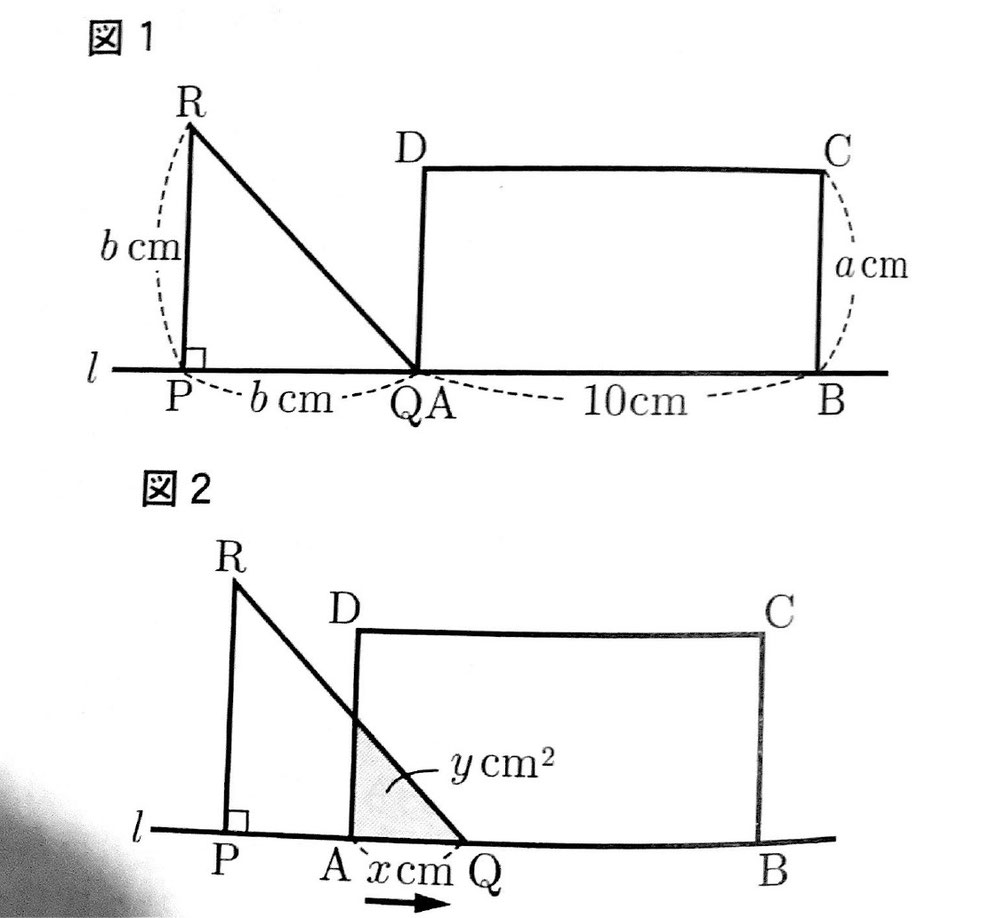
１ a=5,b=6とする。x=3のとき、yの値を求めよ。
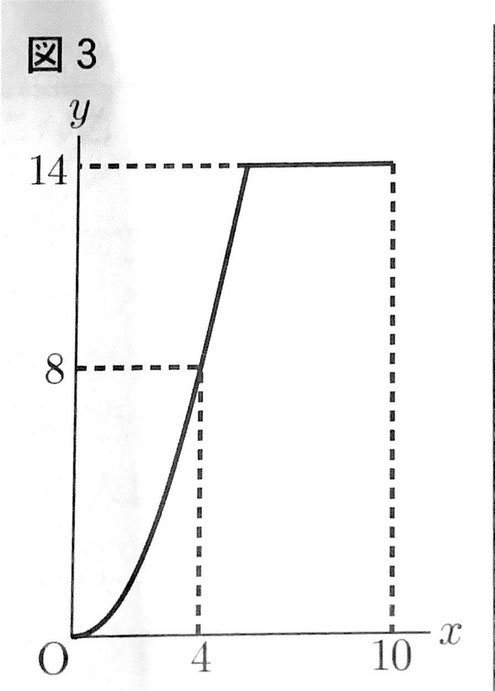
２ xとyの関係が次の図3のようなグラフで表され、0≦ｘ≦4では原点を頂点とする放物線、4≦ｘ≦10では右上がりの直線の一部分と、x軸に平行な直線の一部分であるとき、
（1）0≦ｘ≦4のとき、ｙをｘの式で表せ。
（2）a,bの値をそれぞれ求めよ。
解答
【解答】
１ 【正答 y=9/2】
２（1） 【正答 y=1/2x²】
２（2） 【正答 a=4,b=11/2】
【解説】
１ 求める図形は等しい辺の長さが3ｃｍの直角二等辺三角形になるから、y=1/2×3²=9/2
２（1） （4，8）をグラフが通っているからy=ax²にこれらを代入して、8=16aより、a=1/2。したがって、y=1/2x²
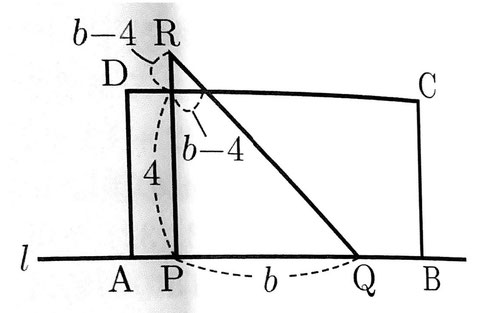
２（2） グラフよりx=4のとき辺RQ上に点Dが重なることがわかる。したがって、a=4。グラフより、点Pが点Aより右側にあるときｙ＝14であることがわかる。また、求める図形は次の図のような台形であるから、1/2×｛(b-4)+b｝×4＝14
これを解いてb=11/2
大問5
問題文
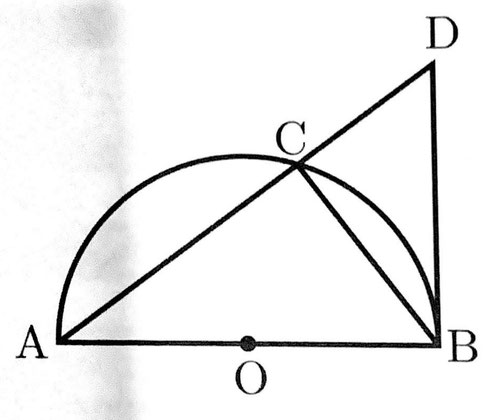
次の図のような、線分ABを直径とする半円Oがある。弧AB上に点Cをとり、直線AC上に点Dを、∠ABD＝90°となるようにとる。このとき、次の問いに答えなさい。（円周率はπを用いること）
１ △ABC∽△BDCであることを証明せよ。
２ AC＝3ｃｍ、CD＝1ｃｍであるとき、
（1）線分BCの長さを求めよ。
（2）線分BDと線分CDと弧BCとで囲まれた部分の面積を求めよ。
解答
【解答】
１ 【正答 下記参照】
２（1） 【正答 √3㎝】
２（2） 【正答 (5√3/4-π/2)㎝²】
【解説】
１
△ABCと△BDCにおいて、
ABは直径より、∠ACB＝∠BCD＝90°…①
△ABCで∠ACB＝90°より、∠BAC＝90°-∠ABC…②
また、∠ABD＝90°より、∠DBC＝90°-∠ABC…③
②、③より、∠BAC＝∠DBC…④
①、④より、2組の角がそれぞれ等しいから。
△ABC∽△BDC
２（1） △ABC∽△BDCより、BC：1＝3：BC BC²＝3 BC＞0より、BC＝√3
２（2） 求める面積は（四角形COBD）-（おうぎ形OBC）＝△DCB+△COB-（√3）²π×1/6＝√3/2+3√3/4-π/2＝5√3/4-π/2
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
