【愛媛県】令和3年度/2021年度入学者高校入試選抜試験：数学
愛媛県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
１ 次の計算をして、答えを書きなさい。
１ (ー３)×５
２ ｘ/２ー２＋(ｘ/５ー１)
３ ２４ｘｙ²÷(ー８ｘｙ)×２ｘ
４ (√３＋√２)(２√３＋√２)＋６/√６
５ (ｘー３)²ー(ｘ＋４)(ｘー４)
解答
１ 【正答 -15】
２ 【正答 7x/10-3】
３ 【正答 -6xy】
４ 【正答 8₊4√6】
５ 【正答 -6x₊25】
大問2
問題文
２ 次の問いに答えなさい。
１ ｘ²ー８ｘ＋１２を因数分解せよ。
２ 気温は、高度が100m増すごとに0.6℃ずつ低くなる。地上の気温が7.6℃のとき、地上から2000ｍ上空の気温は何℃か求めよ。
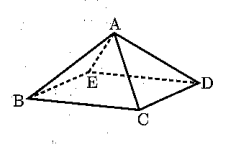
３ 次の図のように、底面が正方形ＢＣＤＥである正四角すいＡＢＣＤＥがある。次のア～キのうち、直線ＢＣとねじれの位置にある直線はどれか。適当なものを全て選び、その記号を書け。
ア 直線AB
イ 直線AC
ウ 直線AD
エ 直線AE
オ 直線BE
カ 直線CD
キ 直線DE
４ あとの表は、あるクラスの13人のハンドボール投げの記録を、大きさの順に並べたものである。この13人と太郎さんを合わせた14人の記録の中央値は、太郎さんを合わせる前の13人の記録の中央値と比べて、１ｍ大きい。
このとき、太郎さんの記録が何ｍか求めよ。
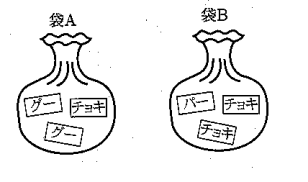
５ 次の図のように、2つの袋A、Bがあり、袋Aの中には、グーのカードが2枚とチョキのカードが1枚、袋Bの中には、チョキのカードが2枚とパーのカードが1枚入っている。太郎さんが袋Aの中から、花子さんが袋Bの中から、それぞれカードを1枚取り出し、取り出したカードでじゃんけんを1回行う。
このとき、あいこになる確率を求めよ。ただし、それぞれの袋について、どのカードが取り出されることも同様に確からしいものとする。
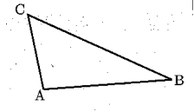
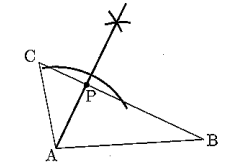
６ 次の図のような△ABCで、辺BCを底辺とみたときの高さをAPとするとき、点Pを作図せよ。ただし、作図に用いた線は消さずに残しておくこと。
７ A地点からＣ地点までの道のりは、Ｂ地点をはさんで13㎞ある。まことさんは、A地点からB地点までを時速３㎞で歩き、B地点で20分休憩した後、B地点からC地点までを時速５㎞で歩いたところ、ちょうど4時間かかった。A地点からB地点までの道のりとB地点からC地点までの道のりを、それぞれ求めよ。ただし、用いる文字が何を表すかを最初に書いてから連立方程式をつくり、答えを求める過程も書くこと。
解答
１ 【正答 (x-2)(x-6)】
２ 【正答 -4.4℃】
３ 【正答 ウ、エ】
４ 【正答 28ｍ】
５ 【正答 9/2】
６ 【正答 下記図】
７ 【正答
A地点からB地点までの道のりをｘ㎞、B地点からC地点までの道のりをｙ㎞とする。
ｘ＋ｙ= 13 ー①
x/3 ＋20/60＋ y/5 = 4 ー②
②より、5x＋3y = 55 －③
③ー①×３より、x = 8
よって、y = 5
答 A地点からB地点までの道のりを８㎞、B地点からC地点までの道のりを５㎞】
大問3
問題文
３ 次の会話文は、太郎さんが、夏休みの自由研究で作ったロボットについて、花子さんと話をしたときのものである。
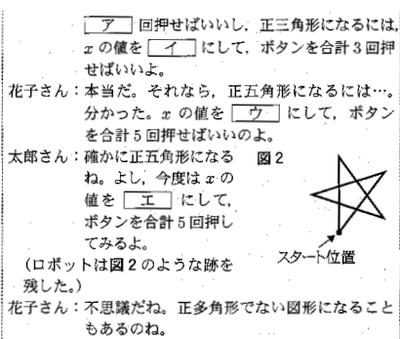
このとき、次の問いに答えなさい。
１ 会話文のア～エに当てはまる数を書け。
２ ロボットの進んだ跡が正多角形となるようなｘの辺りは、全部で何個か求めよ。ただし、ｘは0より大きく180より小さい整数とする。なお、360は正の約数は24個ある。
解答
１ 【正答 ア 4 イ 120 ウ 72 エ 144】
２ 【正答 22個】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
次の図において、放物線①は関数 y = ax² のグラフであり、双曲線は②は y = 16/x のグラフである。放物線①と双曲線②は、点Ａで交わっており、点Ａのｘ座標は4である。また、放物線①上のｘ座標がー２である点をＢとする。
このとき、次の問いに答えなさい。
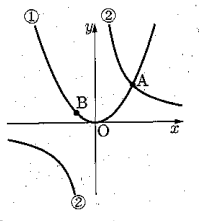
１ 次のア～エのうち、関数 y = 16/x について述べた文として正しいものはどれか。適当なものを１つ選び、その記号を書け。
ア 対応するｘとｙの値の和は一定である。
イ ｘ＜ ０の範囲で、ｘの値が増加すると、ｙの値は減少する。
ウ ｙはｘに比例する。
エ グラフはｙ軸を対象の軸として線対称である。
２ ａの値を求めよ。
３ 直線ABの式を求めよ。
４ 原点Ｏを通り、直線ABに平行な直線と双曲線②との交点のうち、ｘ座標が正である点をＣとする。このとき、△ABCの面積を求めよ。
５ 点Ｐは、ｙ軸上のｙ＞０の範囲を動く点とする。
△ABPの面積と△AOPの面積が等しくなるとき、点Pのｙ座標を全て求めよ。
解答
１ 【正答 イ】
２ 【正答 a = 1/4】
３ 【正答 ｙ= 1/2x＋２】
４ 【正答 ６】
５ 【正答 6/5、6】
大問5
問題文
５ AB = 10㎝、AB ＜ AD の長方形ABCDを、右の図１のように、折り目が点Cを通り、点Bが辺AD上にくるように折り返す。点Ｂが移った点をEとし、折り目を線分CFとすると、AF = 4㎝であった。
このとき、次の問いに答えなさい。
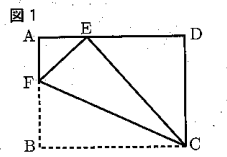
１ △AEF∽△DCEであることを証明せよ。
２ 線分AEの長さを求めよ。
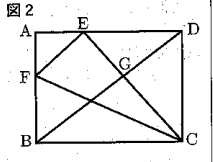
３ 次の図２のように、折り返した部分をもとにもどし、線分CEと線分BDとの交点をGとする。
このとき、四角形BGEFの面積を求めよ。
解答
１ 【正答 △AEFと△DCEにおいて、
四角形ABCDは長方形だから、∠A = 90° ー①
∠FEC = 90°だから、
∠AEF = 180°ー∠FECー∠DEC = 90°ー∠DEC ー②
また、△DCEから∠EDC = 90°より、
∠DCE = 180°ー∠EDC ー∠DEC = 90°ー∠DEC ー③
②、③から∠AEF =∠DCE ー④
①、④から、△AEFと△DCEは二つの角がそれぞれ等しいので、
△AEF∽△DCE 】
２ 【正答 ２√５㎝】
３ 【正答 18√５㎠】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
