【広島県】令和3年度/2021年度入学者高校入試選抜試験：数学
広島県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
国語：解答
問題文
次の（1）～（8）に答えなさい。
（1）6-5-(-2)を計算しなさい。
（2）a=4のとき，6a²÷3aの値を求めなさい。
（3）√2×√6+9/√3を計算しなさい。
（4）方程式x²+5x-6=0を解きなさい。
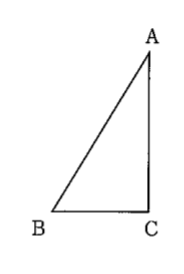
（5）図のように，BC＝3㎝，AC=5㎝，∠BCA＝90°の直角三角形ABCがあります。直角三角形ABCを，辺ACを軸として1回転させてできる立体の体積は何㎤ですか。ただし，円周率はπとします。
（6）2点A（1，7），B（3，2）の間の距離を求めなさい。
（7）右の図の①～③の放射物は、下のア～ウの関数のグラフです。①～③は、それぞれどの関数のグラフですか。ア～ウの中から選び、その記号をそれぞれ書きなさい。
ア y=2x²
イ y=1/3x²
ウ y=-X²
（8）数字を書いた4枚のカード，【1】，【2】，【3】，【4】が袋の中に，数字を書いた3枚のカード，【1】，【2】，【3】が袋の中に入っています。それぞれの袋からカードを1枚ずつ取り出すとき，その2枚のカードに書いてある数の和が6以上になる確率を求めなさい。
解答
（1） 【正答 3】
（2） 【正答 8】
（3） 【正答 5√3】
（4） 【正答 x=-6，1】
（5） 【正答 15π】
（6） 【正答 √29】
（7）① 【正答 イ】
（7）② 【正答 ア】
（7）③ 【正答 ウ】
（8） 【正答 1/4】
大問2
問題文
次の(1)～ (3）に答えなさい。
（1）4＜√a＜13/3に当てはまる整数aの値を全て求めなさい。
（2）下の図のように，線分AB上に点Cがあり，AC=CB=3cmです。線分AC上に点Pをとります。このとき，APを1辺とする正方形の面積とPBを1辺とする正方形の面梢の和は，PCを1辺とする正方形の面積とCBを1辺とする正方形の面梢の和の2倍に等しくなります。このことを，線分APの長さをXcmとして，Xを使った式を用いて説明しなさい。ただし，点Pは点A,Cと重ならないものとします。
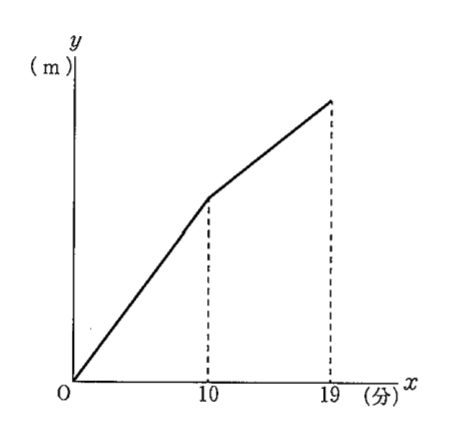
（3）Aさんは駅を出発し，初めの10分間は平らな道を，そのあとの9分間は坂道を歩いて図書館に行きました。下の固は，Aさんが駅を出発してからX分後の駅からの距離をym とし，Xとyの関係をグラフに表したもので，10≦X≦19のときのyをXの式で表すとy= 40x + 280です。Bさんは，Aさんが駅を出発した8分後に自転車で駅を 出発し，Aさんと同じ道を通って，平らな道，坂道ともに分速160mで同書館に行きました。 Bさんはその途中でAさんに追いつきました。BさんがAさんに追いついたのは，駅から何mのところですか。
解答
（1） 【正答 17，18】
（2） 【正答 (例)
APを1辺とする正方形の面積はx²㎠…①
PBを1辺とする正方形の面積は(6-x)²=x²-12x+36(㎠)…②
①,②より、APを1辺とする正方形の面積とPBを1辺とする正方形の面積の和は
x²+x²-12x+36=2x²-12x+36…③
PCを1辺とする正方形の面積は
(3-x)²=x²-6x+9(㎠)…④
CBを1辺とする正方形の面積は9㎠…⑤
④,⑤より、PCを1辺とする正方形の面積とCBを1辺とする正方形の面積の和の2倍は
(x²-6x+9+9)×2＝2ｘ²ー12ｘ+36…⑥
③,⑥より、ＡＰを1辺とする正方形の面積とＰＢを1辺とする正方形の面積の和は、ＰＣを1辺とする正方形の面積とＣＢを1辺とする正方形の面積の和の2倍に等しくなる。】
（3） 【正答 800】
大問3
問題文
下の図のように， AD II BCの台形ABCDがあります。辺BC上に点E, 辺CD 上に点F を， BD II E Fとなるようにとります。また，線分BF と線分EDとの交点を Gとします。 BG:GF =5:2 となるとき，△ABEの面積Sと△ GEF の面積 Tの比を，最も簡単な整数の比で表しなさい。
解答
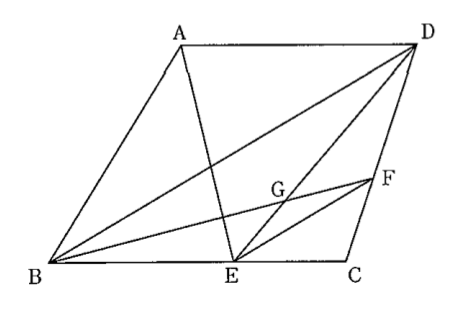
【正答 35：4】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
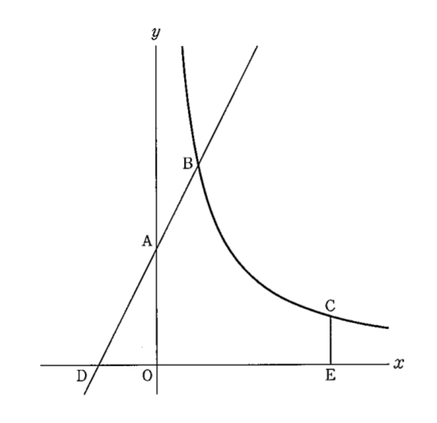
下の図のように，y軸上に点A(0, 5)があり，関数y=a/x含のグラフ上に，y座標が5 より大きい範囲で動く点Bとy座標が 2 である点Cがあります。直線ABとX軸との交点をDとします。また，点CからX軸に垂線を引き，X軸との交点をEとします。ただし， a > 0 とします。
次の(1).(2)に答えなさい。
（1）a=8のとき,点Cのx座標を求めなさい。
（2）DA = AB, DE = 9となるとき，aの値を求めなさい。
解答
（1） 【正答 4】
（2） 【正答 15】
大問5
問題文
A市役所で働いている山本さんと藤井さんは，動画を活用した広報活動を担当しています。山本さんたちは，A市の動画の再生回数を増やすことで，A市の魅力をより多くの人に知ってもらいたいと考えています。そこで，インタネット上に投稿した動画が人気となっているA市出身のXさんーとYさんとZさんのうちの1人に，A市の新しい動画の作成を依頼しようとしています。
山本「A 市が先月投稿した動画の再生回数は，今はどれくらいになっているかな？」
藤井「先ほど確認したところ，今は 1200 回くらいになっていました。 新しい動画では再生回数をもっと増やしたいですね。」
山本「そうだよね。 Xさん，Yさん，Zさんの誰に動画の作成を依頼したらいいかな。」
藤井「まずは， 3 人が投稿した動画の再生回数がどれくらいなのかを調べましょう。」
次の (1) · (2) に答えなさい。
（1）藤井さんは，Xさん，Yさん，zさんが投稿した動画のうち，それぞれの直近50本の動画について再生回数を調べ，下の【資料I】にまとめ，山本さんと話をしています。
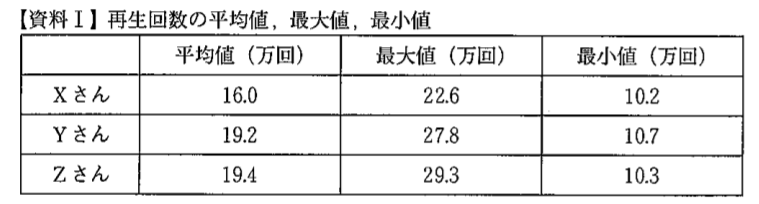
藤井「【資料 I】から， Xさんの再生回数の平均値は， Y さん， Z さんよりも 3 万回以上少ないことが分かりますね。」
山本「そうだね。 それと， ① Xさんについては再生回数の範囲も，Yさん，Zさんよりも小さいね。」
下線部①について，Xさんの再生回数の範囲として適切なものを下のア～工の中から 選び，その記号を書きなさい。
ア 5.8万回
イ 6.6万回
ウ 12.4 万回
エ 32.8万回
（2）山本さんたちは，（1）の【資料I】の分析から，A市の新しい動画の作成をYさんかZさんに依頼することにしました。さらに分析をするために，Yさん，Zさんが投稿した動画 のうち，直近50本の動画の再生回数のヒストグラムを作成し，下の【資料Ⅱ】にまとめました。【資料Ⅱ】のヒストグラムでは，例えば，直近50本の動画の再生回数が10万回以上 12万回未満であった本数が，Yさん，Zさんとも5本ずつあったことを表しています。
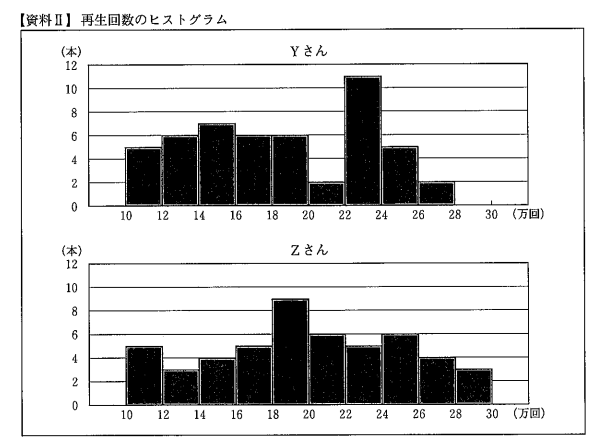
A市の動画の再生回数を増やすために，A市の新しい動画の作成を，あなたなら，Yさんと Zさんのどちらに依頼しますか。また，その人に依頼する理由を，【資料l1】のYさんと zさんのヒストグラムを比較して，そこから分かる特徴を基に，数値を用いて説明しなさい。
解答
（1） 【正答 ウ】
（2） 【正答 (例)
（Yさんに依頼する場合）
再生回数の最頻値に着目すると、Yさんは23万回、ｚさんは19万回なので、Ｙさんが作成する動画の方が、Ｚさんが作成する動画より再生回数が多くなりそうである。だから、Ｙさんに依頼する。
（Ｚさんに依頼する場合）
再生回数が18万回以上の階級の度数の合計に着目すると、Ｙさんは26本、Ｚさんは33本なので、Ｚさんが作成する動画の方が、Ｙさんが作成する動画より再生回数が多くなりそうである。だから、Ｚさんに依頼する。】
大問6
問題文
中学生の航平さんは，「三角形の3つの辺に接する円の作図」について，高校生のお兄さんの啓太さんと話をしています。
航平「数学の授業で，先生から，これまで学習したことを用いると，三角形の 3 つの辺に接する円を作図できると聞いたんだけど，どうやったら作図できるんだろう。」
啓太「①角の二等分線の作図と②垂線の作図の方法を知っていれば，その円を作図できるよ。」
航平「その 2 つの方法は習ったし，角の二等分線の作図の方法が正しいことも証明したよ。」
啓太「そうなんだね。実は，三角形の 2 つの角の二等分線の交点が，その円の中心になるんだよ。 三角形の 3 つの辺に接する円の作図には，いろいろな図形の性質が用いられているから，作図をする際には振り返るといいよ。」
次の(1)～ （3)に答えなさい。
(1)下線部①について，航平さんは，下の【角の二等分線の作図の方法】を振り返りました。
【角の二等分線の作図の方法】において，作固した半直線ORが ∠XOYの二等分線であることを，三角形の合同条件を利用して証明しなさい。
(2)下線部②について，航平さんは，右の図の△ABCにおいて，∠ABC, ∠ACB の二等分線をそれぞれ引き， その交点をIとしました。そして，下の 【手順】によって点Iから辺BCに垂線を引きました。
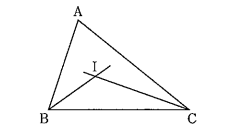
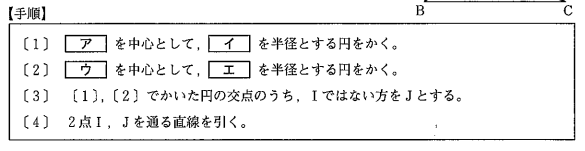
【手順】の【ア】・【ウ】に当てはまる点をそれぞれ答えなさい。また，【イ】・【エ】 に当てはまる線分をそれぞれ答えなさい。
航平さんは，点Iから辺BCに引いた垂線と辺BCとの交点をDとしました。同じようにして， 点Iから辺CA,ABにも垂線を引き，辺CA,ABとの交点をそれぞれE,Fとしました。
そして，角の二等分線の性質から ID=IE=IF であり，点 I を中心とし，IDを半径とする円が，円の接線の性質から△ABCの3つの辺に接する円であることが分かりました。
(3) さらに，航平さんは，コンピュ ー タを使って△ABCの 3 つの辺に接する円をかき，下の図のように，辺BCをそのままにして点Aを動かし，△ABCをいろいろな形の三角形に変え， いつでも成り立ちそうなことがらについて調べました。
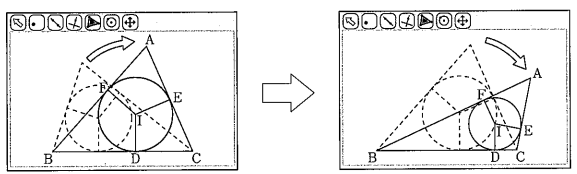
航平さんは，下の図のように，∠BACの大きさを，鋭角，直角，鈍角と変化させたときの△DEFに着目しました。
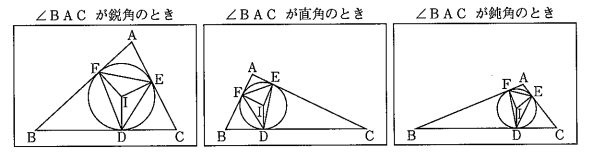
航平さんは，△ABCがどのような三角形でも，△DEFが鋭角三角形になるのではない だろうかと考え，それがいつでも成り立つことを，下のように説明しました。
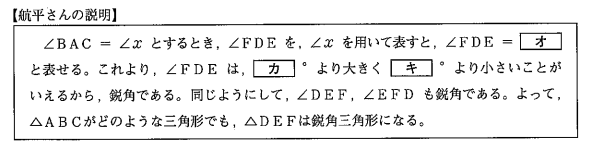
【航平さんの説明】の【オ】に当てはまる式を，∠Xを用いて表しなさい。また，【カ】· 【キ】に当てはまる数をそれぞれ求めなさい。
解答
（1） 【正答 (例)
点Pと点R、点Qと点Rをそれぞれ結ぶ。
△PORと△QORにおいて
OP=OQ…①
PR=QR…②
共通な辺であるから
OR=OR…③
①、②、③より、3組の辺がそれぞれ等しいから
△POR=△QOR
合同な図形の対応する角は等しいから
∠POR=∠QOR】
したがって、ORは∠XOYの二等分線である。
（2）ア 【正答 B】
（2）イ 【正答 BI】
（2）ウ 【正答 C】
（2）エ 【正答 CI】
（3）オ 【正答 90°-1/2∠x】
（3）カ 【正答 0】
（3）キ 【正答 90】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
