







兵庫県の2021年3月実施の令和3年度(2021年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の兵庫県の数学は6つの大問で構成され、小問集合・連立方程式・図形・関数・確率・法則性を問う問題の構成になっています。後に行けば行くほど難しくなるお手本のような形式です。
難易度自体は例年よりも簡単でやや難でした。大問2までは完全解答を目指しましょう。逆に大問6はかなりの難問になっているので数学に自信がある方は一度挑戦してみてください。
【兵庫県】令和3年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら>>
問1:-7-(-2) を計算しなさい。
問2:-6x²y÷2xy を計算しなさい。
問3:4√5 – √20 を計算しなさい。
問4:x²-4y² を因数分解しなさい。
問5:2次方程式 x²-3x-5=0 を解きなさい。
問6:半径2㎝の球の表面積は何㎠か、求めなさい。ただし、円周率はπとする。
問7:図で、l // m のとき、∠xの大きさは何度か、求めなさい。
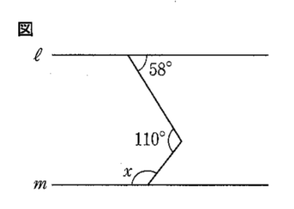
問8:表はある中学校の生徒25人がそれぞれの家庭から出るごみの量について調べ、その結果を度数分布表にまとめたものである。中央値(メジアン)が含まれる階級の相対度数を求めなさい。
ただし、小数第2位までの小数で表すこと。
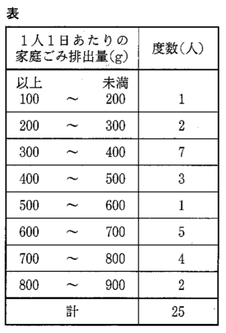
AさんとBさんが同時に駅を出発し、同じ道を通って、2700m離れた博物館に向かった。
Aさんは自転車に乗り、はじめは分速160mで走っていたが、途中のP地点で自転車が故障し、P地点から自転車を押して、分速60mで歩き、駅を出発してから35分後に博物館に到着した。
Bさんは駅から走り、Aさんより5分早く博物館に到着した。
図は、Aさんが駅を出発してからの時間と距離の関係を表したものである。ただし、Aさんが自転車で走る速さ、Aさんが歩く速さ、Bさんが走る速さは、それぞれ一定とする。
次の問いに答えなさい。
問1:Bさんが走る速さは分速何mか、求めなさい。
問2:Aさんが自転車で走った時間と歩いた時間を、連立方程式を使って、次のように求めた。
【 ア 】に当てはまる数式を書き、【イ】【ウ】に当てはまる数をそれぞれ求めなさい。
Aさんが自転車で走った時間をa分、歩いた時間をb分とすると、
・a + b=35
・【 ア 】=2700
これを連立して解くと、a=【イ】、b=【ウ】
この解は問題に合っている。
Aさんが自転車で走った時間は【イ】分、歩いた時間は【ウ】分である。
問3:BさんがAさんに追いつくのは、駅から何mの地点か、求めなさい。
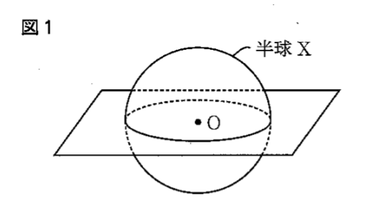
図1のように、ある球をその中心Oを通る平面で切ると半球が2つでき、その一方を半球Xとする。
このとき、切り口は中心がOの円となる。この円Oの周上に、図2のように、3点A,B, Cを∠BAC=120°となるようにとり、∠BACの二等分線と線分BC、円周との交点をそれぞれD, Eとすると、AE=8cm、BE=7cmとなった。
次の問いに答えなさい。
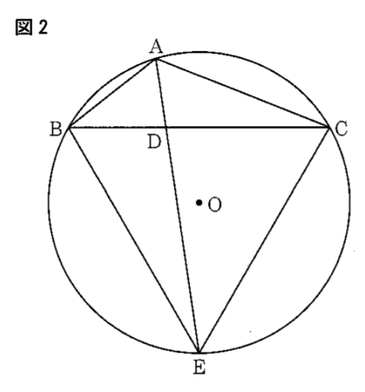
問1:△ABE∽△BDEを次のように証明した。
【ⅰ】と【ⅱ】にあてはまるものを、あとのア~カからそれぞれ1つ選んでその符号を書き、この証明を完成させなさい。
〈照明〉
△ABEと△BDEにおいて、
共通な角だから、
∠AEB=∠BED …①
直線AEは∠BACの二等分線だから
∠BAE=∠【ⅰ】 …②
弧CEに対する円周角は等しいから、
∠DBE=∠【ⅰ】 …③
②、③より、∠BAE=∠DBE …④
①、④より、【ⅱ】から、
△ABE∽△BDE
ア ABC
イ CDE
ウ CAE
エ 3組の辺の比がすべて等しい
オ 2組の辺の比とその間の角がそれぞれ等しい
カ 2組の角がそれぞれ等しい
問2:線分DEの長さは何㎝か、求めなさい。
問3:△BCEの面積は何㎠か、求めなさい。
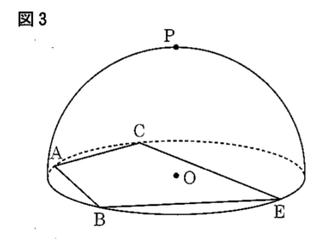
問4:図3のように、半球Xの球面上に、点Pを直線POが平面ABECに垂直となるようにとる。このとき、頂点がP、底面が四角形ABECである四角すいの体積は何㎠か、求めなさい。
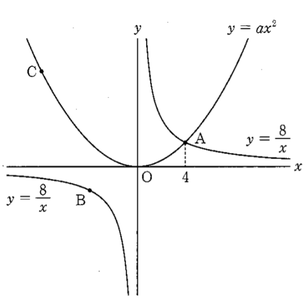
図のように関数 y=8/x のグラフ上に2点A,Bがあり、点Aのx座標は4、線分ABの中点は原点Oである。また、点Aを通る関数 y=ax²のグラフ上に点Cがあり、直線CAの傾きは負の数である。
問1:点Bの座標を求めなさい。
問2:aの値を求めなさい。
問3:点Bを通り、直線CAに平行な直線と、y軸との交点をDとすると、△OACと△OBDの面積比は3:1である。
① 次の【ア】~【ウ】にあてはまる数をそれぞれ求めなさい。
点Cのx座標は、【ア】である。また、関数y=ax²について、xの変域が【ア】≦x≦4 のときのyの変域は【イ】≦y≦【ウ】である。
② x軸上に点Eをとり、△ACEをつくる。△ACEの3辺の長さの和が最小となるとき、点Eのx座標を求めなさい。
6枚のメダルがあり、片方の面にだけ、1,2,4,6,8,9の数がそれぞれ1つずつ書かれている。
ただし、6と9を区別するため、6は6、9は9と書かれている。
数が書かれた面を表、書かれていない面を裏とし、メダルを投げたときは必ずどちらかの面が上になり、どちらの面が上になることも同様に確からしいものとする。
この6枚のメダルを同時に1回投げるとき、次の問いに答えなさい。
問1:2枚が表で4枚が裏になる出方は何通りあるか、求めなさい。
問2:6枚のメダルの表裏の出方は、全部で何通りあるか、求めなさい。
問3:表がでたメダルに書かれた数をすべてかけ合わせ、その値をaとする。ただし、表が1枚も出なかったときは、a=0とし、表が1枚出たときは、そのメダルに書かれてた数をaとする。
①表が出たメダルが1枚または2枚で、√aが整数になる表裏の出方は何通りあるか、求めなさい。
②√aが整数になる確率を求めなさい。
つばささんとあおいさんは、写真のような折り紙を折ったときにできた星形の模様を見て、図1の図形に興味をもった。
次の文章は、2人が図1の図形について調べ、話し合いをしている場面である。
つばさ:図1の図形は星形正八角形というみたいだね。調べていたら、星形正n角形のかき方を見つけたよ。
〈星形正n角形(n≦5)のかき方〉
円周をn等分する点をとり、1つの点から出発して、すべての点を通ってもとの点に戻るように、同じ長さの線分で点と点を順に結ぶ。このかき方でかいた図形が正n角形になる場合があるが、正n角形は星形正n角形ではない。
あおい:最初に星形正五角形をかいてみよう。図2のように、円周を5等分する点をとり、1つの点から出発して隣り合う点を順に結ぶと、正五角形になるから、星形正五角形ではないね。また、図3のように、1つの点から点を2つ目ごとに結んでみよう。すべての点を通ってもとの点に戻るから、この図形は星形正五角形だね。
つばさ:1つの点から点を3つ目ごとに結んでも、星形正五角形がかけるね。4つ目ごとに結ぶと、正五角形になるから、星形正五角形ではないね。
あおい:次は、星形正六角形をかいてみよう。円周を6等分する点を、1つの点から2つ目ごとに結ぶと、もとの点に戻ったときに図4のようになって、すべての点を通っていないからかけないね。3つ目ごとに結ぶと図5のようになって、4つ目ごとに結ぶと図4のようになるから、星形正六角形はかけないね。
つばさ:星形正七角形は円周を7等分する点を、1つの点から2つ目ごとに結んでも、3つ目ごとに結んでもかけるね。この2つは、形が異なる図形だね。
あおい:点を4つ目ごとに結ぶと、3つ目ごとに結んだときと同じ形の図形がかけるね。5つ目ごとに結ぶと…
つばさ:点を2つ目ごとに結んだときと同じ形の図形がかけるはずだよ。
あおい:そうだね。同じ形の図形は1種類として数えると、円周を7等分する点をとった場合、星形正七角形は2種類かけるね。
2人はその他にも星形正n角形をかき、その一部を表にまとめた。
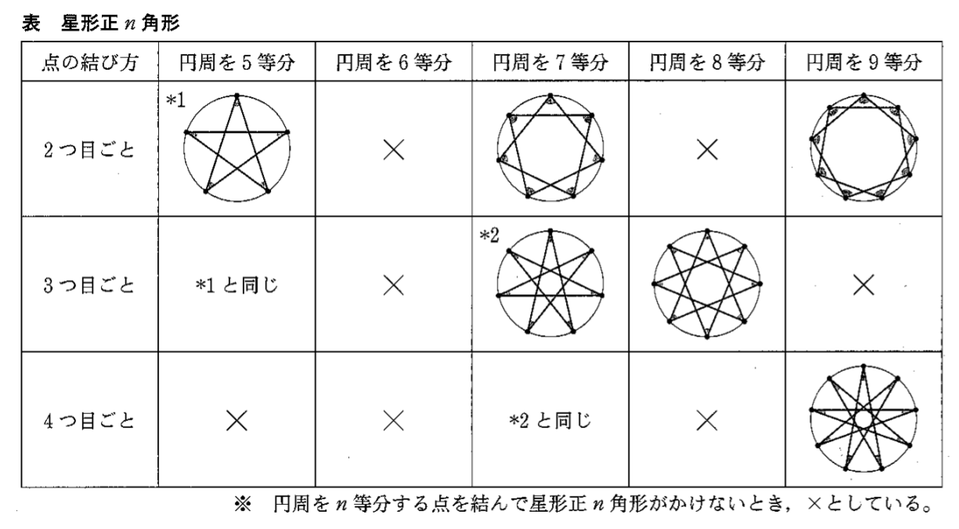
次の問いに答えなさい。
問1:次のア~ウのうち、円周をn等分する点をとり、その点を2つ目ごとに結んで星形正n角形を書くことができる場合はどれか、1つ選んでその符号を書きなさい。
ア 円周を10等分する点をとる
イ 円周を11等分する点をとる
ウ 円周を12等分する点をとる
問2:円周を7等分する点を、2つ目のごとに結んでできる星形正七角形の先端部分の7個の角の和の求め方を、つばささんは次のように説明した。【①】【②】にあてはまる数をそれぞれ求めなさい。
つばさ:図1の図形は星形正八角形というみたいだね。調べていたら、星形正n角形のかき方を見つけたよ。
図6のように、先端部分の1個の角の大きさをx度として、先端部分の7個の角の和7x度を求めます。円周角の大きさがx度の弧に対する中心角の大きさは2x度で、おうぎ型の弧の長さは中心角の大きさに比例するので、図7から、
【①】:7=2x:360
比例式の性質を用いて7xを求めると、
7×2x=【①】×360
7x=【②】
したがって、先端部分の7個の角の和は【②】度です。
問3:円周をn等分する点を、2つ目ごとに結んでできる星形正n角形の先端部分のn個の角の和は何度か、nを用いて表しなさい。ただし、nは5以上の整数で、星形正n角形がかけないnは除くものとする。
問4:円周を24等分する点をとった場合、星形正二十四角形は何種類書くことができるか、求めなさい。また、それらの先端部分の1個の角について、その大きさが最も小さいものは何度か、求めなさい。ただし、同じ形の図形は1種類として数えることとする。
問1:-5
問2:-3x
問3:2√5
問4:(x+2y)(x-2Y)
問5:(3±√29)/2
問6:16π㎠
問7:128度
問8:0.12
問1:分速90m
問2:ア: 160a + 60b、イ: 6、ウ: 29
問3:1800m
問1:ⅰウ ⅱカ
問2:49/8㎝
問3:(49√3)/4㎠
問4:112/3㎠
問1:(-4,-2)
問2:a=1/8
問3:①ア-8 イ0 ウ8 ②8/5
問1:15通り
問2:64通り
問3:①7通り ②1/4
問1:イ
問2:①3 ②540
問3:180(n-4)度
問4:3種類、15度
問1:-7-(-2) を計算しなさい。
【答え:-5】
負の符号は2つ続くと、正の符号になります。
問2:-6x²y÷2xy を計算しなさい。
【答え:-3x】
数字と文字で分けて考えましょう。
問3:4√5 – √20 を計算しなさい。
【答え:2√5 」】
√20=2√5 であるから、
4√5 – √20 = 4√5 – 2√5 = 2√5
問4:x²-4y² を因数分解しなさい。
【答え:(x+2y)(x-2Y) 】
符号がマイナスであることと、どちらの係数も二乗した数であるので、このような因数分解となります。
問5:2次方程式 x²-3x-5=0 を解きなさい。
【答え:(3±√29)/2 】
2次方程式の解の公式を使って解きます。
問6:半径2㎝の球の表面積は何㎠か、求めなさい。ただし、円周率はπとする。
【答え:16π㎠ 】
球の表面積は、4πr² でも求めることができます。
したがって、4π×2²
問7:図で、l // m のとき、∠xの大きさは何度か、求めなさい。
【答え:128度 】
問8:表はある中学校の生徒25人がそれぞれの家庭から出るごみの量について調べ、その結果を度数分布表にまとめたものである。中央値(メジアン)が含まれる階級の相対度数を求めなさい。
ただし、小数第2位までの小数で表すこと。
【答え:0.12 】
まず、中央値が含まれる階級を探す。
生徒は25人であるから、中央値は上から(下からでも良い)13番目の値で、表を見ると、400~500の階級であることが分かる。
次に、その階級の相対度数を求める。よって、
3÷25=0.12
問1:Bさんが走る速さは分速何mか、求めなさい。
【答え:分速90m 】
BさんはAさんより5分早く到着したため、30分で到着したことが分かる。
したがって、2700÷30=90 より、 分速90m
Aさんが自転車で走った時間をa分、歩いた時間をb分とすると、
・a + b=35
・【 ア 】=2700
これを連立して解くと、a=【イ】、b=【ウ】
この解は問題に合っている。
Aさんが自転車で走った時間は【イ】分、歩いた時間は【ウ】分である。
【答え:ア: 160a + 60b、イ: 6、ウ: 29 】
問題文より、博物館に到着した時間(=走った時間と歩いた時間の合計)は、35分だとわかるので、1つ目の式はこれを示している。
2つ目の式は、博物館への距離(=走った距離と歩いた距離の合計)が2700mだという事を示している。
分速160mでa分間、分速60mでb分間移動しています。
次に、この二つの式を連立して解くと、【イ】【ウ】を求めることができます。
a + b=35 …①
160a + 60b=2700 …②
②÷10より、16a + 6b=270 …②’
①×6より、6a + 6b =210 …①’
②’ー①’より、10a = 60
したがって、a=6、b=29
問3:BさんがAさんに追いつくのは、駅から何mの地点か、求めなさい。
【答え:1800m 】
P地点までには明らかにAさんが早いので、追いつきません。
そのため、追いつくのはAさんが自転車を押し歩いているときです。
そこで、出発してからx分後に追いついた(AさんとBさんの移動距離が等しくなる)とすると、
160×6+60(x-6)=90x
これを解いて、 x=20
証明全体を見ると、角度のみに言及しており、辺の比について言及していないことがわかる。
したがって、相似の条件の中でも、「2つの角がそれぞれ等しい」を使用することがわかる。
【答え:49/8㎝】
△ABE∽△BDEを活用します。
BE:DE=AE:BE
7:DE=8:7
8DE=49
DE=49/8
【答え:(49√3)/4㎠ 】
正三角形だということに気付き、面積を計算する問題である。
∠BAC=120°であり、直線AEが∠BACの二等分線であることがポイントである。
つまり、∠BAE=∠EAC=60°
弧BEに対する円周角より、
∠BAE=∠BCE=60°
弧CEに対する円周角より、
∠CAE=∠CBE=60°
したがって、△BCEは一辺が7㎝の正三角形である。
1辺が7㎝の正三角形の高さは、(7√3)/2 ㎝である。
△BCEの面積は、
7×(7√3)/2×1/2=(49√3)/4
【答え:112/3㎠】
四角すいの体積を求めるには、底面の面積と高さがわかればよい。
まず、底面の面積を考える。
△BCEの面積と、AEとDEの長さがわかっていることがポイントである。
BCを底辺とすると、△BCEと△ABCは同じ底辺を持っていることがわかる。
また、AD:DE=(8-49/8):49/8=15:49であるから、
四角形ABEC=△BCE× (15+49)/49=(49√3)/4 × 64/49=16
次に、高さを考える。
高さは、球の半径(OP)となるので、円Oの半径とも等しい。
△BCEの高さより、円Oの半径を求めると、(7√3)/2×2/3=(7/√3)/3
以上から、求める四角すいの面積は
16√3 × (7/√3)/3 × 1/3 = 112/3
【答え:(-4,-2)】
点A(4,2)である。 線分ABの中点が原点Oであるから、点Aのx座標に-を付ける。
【答え:a=1/8 】
点Aを通るので代入して、
2=a×4²
2=16a
a=1/8
【答え:①ア-8 イ0 ウ8 ②8/5 】
①直線ACとy軸の交点をD’とすると、
OD=OD’であり、△ODBと△OD’Aの面積は等しい。
△OAC:△ODB=3:1
(△OD’A+△OD’C):△ODB=3:1であることと考えると、
△OD’C:△OD’A=2:1
底辺をOD’だとすると、高さ(x座標の絶対値)の比が面積比と同じになるので、
点Cのx座標の絶対値:点Aのx座標の絶対値=2:1
点Cのx座標の絶対値:4=2:1
したがって、点Cのx座標の絶対値は8
直線CAの傾きは負の数であるから、点Cのx座標は-8
よって、点C(-8, 8)
y=1/8x²で-8≦x≦4のとき、
yの最小値はx=0のとき0
yの最大値はx=-8のとき8
②△AECの3辺の和が最小となるのは、AE+ECが最小となればよい。
Cのx軸に関する対称点をC’(-8,-8)とすると、EC=EC’
したがって、AE+EC’が最小となるEを探せばよい。
最小となるのは、3点A, E, C’が一直線上に並ぶときである。
直線AC’の方程式を求め、点E(直線上でy座標が0の点)を求めていく。
直線AC’は、y=5/6x-4/3 である。
よって、点E(8/5, 0)
【答え:15通り】
6C2=15
【答え:64通り】
26=64
【答え:①7通り ②1/4】
4=22, 6=2×3, 8=23, 9=32 と整理しておくと良い。
①表が1枚のときに√aが整数になるのは、1, 4, 9が出る時なので3通り。
表が2枚のときに√aが整数になるのは、(1,4)(1,9)(2,8)(4,9)の4通り。
以上から7通り。
②表が3枚のときに√aが整数になるのは、(1,2,8)(1、4,9)(2,4,8)(2,8,9)の4通り。
表が4枚のときに√aが整数になるのは、(1,2,4,8)(1,2,8,9)(2,4,8,9)の3通り。
表が5枚のときに√aが整数になるのは、(1,2,4,8,9)の1通り。
表が6枚のときに√aが整数になることはない。
また、表が0の時、a=0で当てはまるので1通り。
したがって、3+4+4+3+1+1=16通り。
よって、求める確率は16/64=1/4
【答え:イ】
等分した点を0,1,2,3,4…として考える。
ア 0-2-4-6-8-0と進むので戻ってしまい、正五角形となり、星形はできない。
イ 0-2-4-6-8-10-1-3…と進むので星形ができる。
ウ 0-2-4-6-8-10-0と進むので戻ってしまい、正六角形となり、星形はできない。
【答え::①3 ②540】
①図を見ると、2xの中心角をもつおうぎ形は3区切り分の弧を持っている。
【答え:180(n-4)度】
問2と同様に考えてみると、
n=5のとき
1:5=2x:360°
n=7のとき
3:7=2x:360°
n=9のとき
5:9=2x:360°
このようにみると傾向がある事が分かる。
円周をn等分し、そのうちの(n-4)個分を弧にもつおうぎ形の中心角が2x度である。したがって、円周全てはn個分で中心角が360度であることから、
(n-4):n = 2x:360°
2nx=360(n-4)
nx=180(n-4)
【答え:3種類、15度】
等分した点を0,1,2,3,4…23として考える。
そして、2つ目ごと、3つ目ごと、…11つ目ごとに点を結ぶ場合を考える。
24の約数である、2,3,4,6,8は正n角形ができてしまうので星形にならない。
では、他の場合において、線で結ぶ点の動きを見ていく。
5つ目ごと
0-5-10-15-20-1-6-11-…で星形になる。
7つ目ごと
0-7-14-21-4-11-18-…で星形になる。
9つ目ごと
0-9-18-3-12-21-6-15-0となり星形にならない。
10つ目ごと
0-10-20-6-16-2-12-22-8-18-4-14-0となり星形にならない。
11つ目ごと
0-11-22-9-20-7-18-5-16-3-…で星形になる。
以上から、5,7,11つ目ごとに点を結ぶときに星形になる。
先端部分の角が元も小さくなるのは11個目ごとに結んだ時である。問2と同様に考えていく。
先端部分の1個の角をx度とすると、円周を24等分した際の区切り2個分の弧をもつおうぎ形の中心角が2x°であること、
円周すべて(24個分)のときは中心角が360°であることから比例式をつくると、
2:24=2x:360
これを解いて、x=15
家庭教師のやる気アシストは、兵庫県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

