【神奈川県】令和5年度/2023年度入学者高校入試選抜試験：数学の解説
神奈川県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1 小問集合
問題文
次の計算をした結果として正しいものを、それぞれあとの1～4の中から1つずつ選び、その番号を答えなさい。
（ア）$-1-(-7)$
1：$-8$
2：$-6$
3：$6$
4：$8$
（イ）$-\frac{3}{7}+\frac{1}{2}$
1：$-\frac{13}{14}$
2：$-\frac{1}{14}$
3：$\frac{1}{14}$
4：$\frac{13}{14}$
（ウ）$12ab^2\times6a\div(-3b)$
1：$-24a^2b$
2：$-24ab^2$
3：$24a^2b$
4：$24ab^2$
（エ）$\frac{3x+2y}{7}-\frac{2x-y}{5}$
1：$\frac{x-17y}{35}$
2：$\frac{x-3y}{35}$
3：$\frac{x+3y}{35}$
4：$\frac{x+17y}{35}$
（オ）$(\sqrt{6}+5)^2-5(\sqrt{6}+5)$
1：$6-5\sqrt{6}$
2：$6+5\sqrt{6}$
3：$6+10\sqrt{6}$
4：$6+15\sqrt{6}$
解答・解説
（ア）3
（与式）=$-1+7=6$
（イ）3
（与式）=$-\frac{6}{7}\frac{7}{14}=\frac{1}{14}$
（ウ）1
分数の形にして通分すると計算がしやすい。
（与式）=$-\frac{12ab^2\times6a}{3b}=-24a^2b$
（エ）4
（与式）=$\frac{5(3x+2y)-7(2x-y)}{35}=\frac{x+17y}{35}$
（オ）2
一度因数分解をすると計算が楽になる。
（与式）=$\sqrt{6}(\sqrt{6}+5)=6+5\sqrt{6}$
大問2 小問集合
問題文
次の問いに対する答えとして正しいものを、それぞれあとの1～4の中から1つずつ選び、その番号を答えなさい。
（ア）$(x-5)(x+3)-2x+10$を因数分解しなさい。
1：$(x-3)(x+3)$
2：$(x-5)(x+1)$
3：$(x-5)(x+5)$
4：$(x+5)(x-1)$
（イ）二次方程式$7x^2+2x-1=0$を解きなさい。
1：$x=\frac{-1\pm2\sqrt{2}}{7}$
2：$x=\frac{-1\pm4\sqrt{2}}{7}$
3：$x=\frac{1\pm2\sqrt{2}}{7}$
4：$x=\frac{1\pm4\sqrt{2}}{7}$
（ウ）関数$y=-2x^2$について、xの値が-3から-1まで増加するときの変化の割合を求めなさい。
1：$-8$
2：$-4$
3：$4$
4：$8$
（エ）十の位の数が4である3桁の自然数がある。この自然数の、百の位の数と一の位の数の和は10であり、百の位の数と一の位の数を入れ替えた数はこの自然数より396大きい。
このとき、この自然数の一の位の数を求めなさい。
1：$6$
2：$7$
3：$8$
4：$9$
（オ）$\frac{3780}{n}$が自然数の平方となるような、最も小さい自然数nの値を求めなさい。
1：$n=35$
2：$n=70$
3：$n=105$
4：$n=210$
解答・解説
（ア）2
一度展開をしてから、因数分解を行う。
（与式）=$x^2-2x-15-2x+10=x^2-4x-5=(x-5)(x+1)$
（イ）1
解の公式を用いて解けばよい。
（与式）=$x=\frac{-2\pm\sqrt{2^2-4\times7\times(-1)}}{2\times7}=\frac{-1\pm\sqrt{1-\times7\times(-1)}}{7}=\frac{-1\pm2\sqrt{2}}{7}$
（ウ）4
変化の割合は$\frac{yの増加量}{xの増加量}$で求めることができるので、
$\frac{-18-(-2)}{-3-(-1)}=\frac{-16}{-2}=8$
（エ）2
3桁の数を$a4b$とすると、問題文から二つの式を得られる。
①$a+b=10$
②$(100b+40+a)-(100a+40+c)=396$
これら二つの式を連立方程式で解くと、$(a,b)=(3,7)$となる。
（オ）3
3780を因数分解すると$2^2\times3^3\times5\times7$となるので、平方を作るためには$3\times5\times7=105$をnに入れればよい。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3 中問集合
問題文
次の問いに答えなさい。
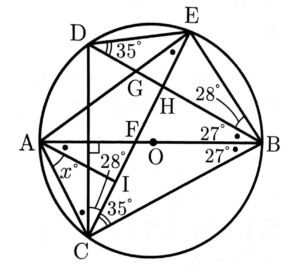
（ア）次の図1のように、線分ABを直径とする円Oの周上に、2点A,Bとは異なる点Cを、AC<BCとなるようにとり、点Cを含まない弧AB上に点Dを、∠ABC=∠ABDとなるようにとる。
また、点Aを含まない弧BD上に、2点B,Dとは異なる点Eをとり、線分ABと線分CEとの交点をF、線分AEと線分BDとの交点をG、線分BDと線分CEとの交点をHとする。
さらに、線分CE上に点Iを、DB//AIとなるようにとる。
このとき、次の（ⅰ）（ⅱ）に答えなさい。
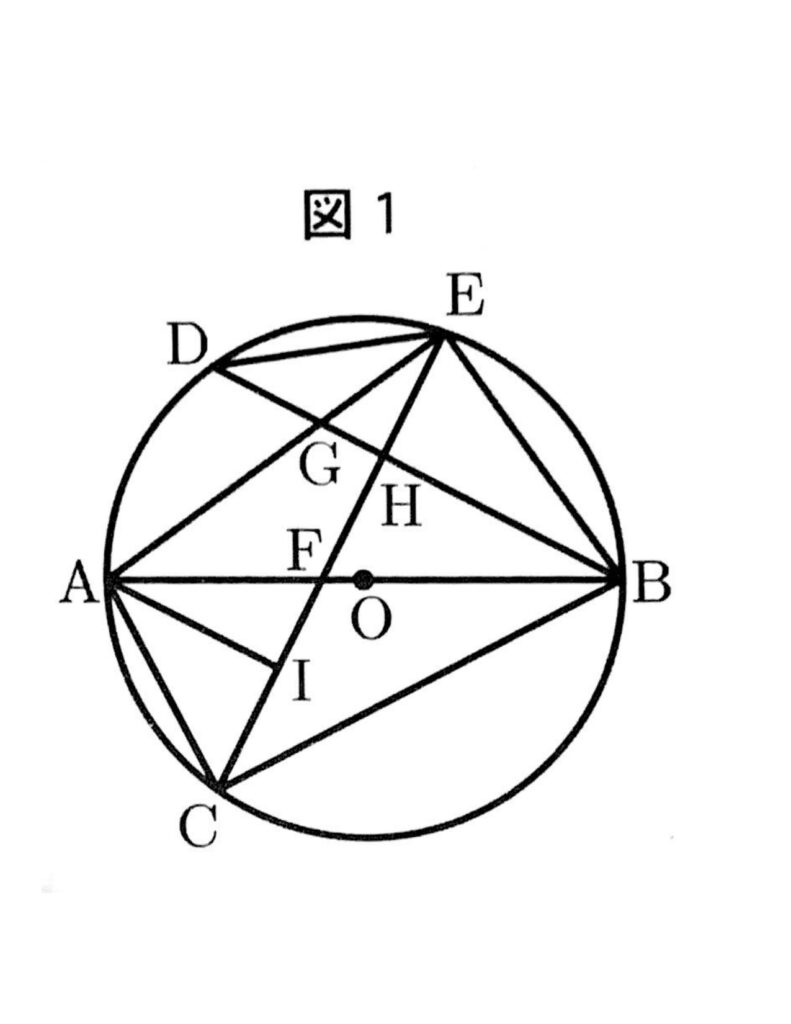
（ⅰ）三角形AIFと三角形EHGが相似であることを次のように証明した。(a)～(c)に最も適するものを、それぞれ選択肢の1～4の中から1つずつ選び、その番号を答えなさい。
[証明]
△AIFと△EHGにおいて、
まず、DB//AIより、平行線の同位角は等しいから、
(a)
よって、∠AIF＝∠EHG・・・①
次に、仮定より、
∠ABC＝∠ABD・・・②
また、弧ACに対する円周角は等しいから、
∠ABC＝∠AEC・・・③
さらに、DB//AIより、平行線の錯角は等しいから、
(b)・・・④
②、③、④より、∠AEC＝∠BAI
よって、∠FAI＝∠GEH・・・⑤
①、⑤より、(c)から、
△AIF∽△EHG
(a),(b)の選択肢
1：∠ABD＝∠BAI
2：∠AIE＝∠BHC
3：∠AIE＝∠DHE
4：∠EAI＝∠EGB
(c)の選択肢
1：1組の辺とその両端の角がそれぞれ等しい
2：2組の辺の比とその間の角がそれぞれ等しい
3：3組の辺の比がすべて等しい
4：2組の角がそれぞれ等しい
（ⅱ）次の【 】の中の「あ」「い」にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その数字を答えなさい。
∠BDE＝35°、∠DBE＝28°のとき、∠CAIの大きさは【あい】°である。
（イ）ある中学校で1学年から3学年まであわせて10クラスの生徒が集まり生徒総会を開催した。生徒総会では生徒会から3つの議案X,Y,Zが提出され、それぞれの議案について採決を行った。
次の資料1は議案Xに賛成した人数を、資料2は議案Yに賛成した人数を、それぞれクラスごとに記録したものである。資料3は議案Zに賛成した人数をクラスごとに記録し、その記録の平均値、中央値、四分位範囲をまとめたものである。
このとき、次の（ⅰ）（ⅱ）に答えなさい。
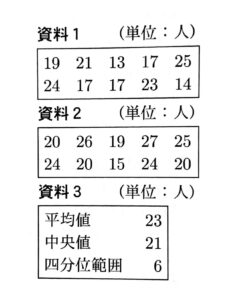
（ⅰ）資料1の記録を箱ひげ図に表したものとして最も適するものを次の1～4中から1つ選び、その番号を答えなさい。
（ⅱ）資料2と資料3から読み取れることがらを、次のA～Dの中からすべて選んだ時の組み合わせとして最も適するものを次の1～6中から1つ選び、その番号を答えなさい。
A：議案Yに賛成した人数の最頻値は20人である。
B：賛成した人数の合計は、議案Zより議案Yの方が多い。
C：賛成した人数の中央値は、議案Zより議案Yの方が大きい。
D：賛成した人数の四分位範囲は、議案Zより議案Yの方が小さい。
1：A,B 2：A,C 3：B,D
4：C,D 5：A,B,C 6：A,C,D
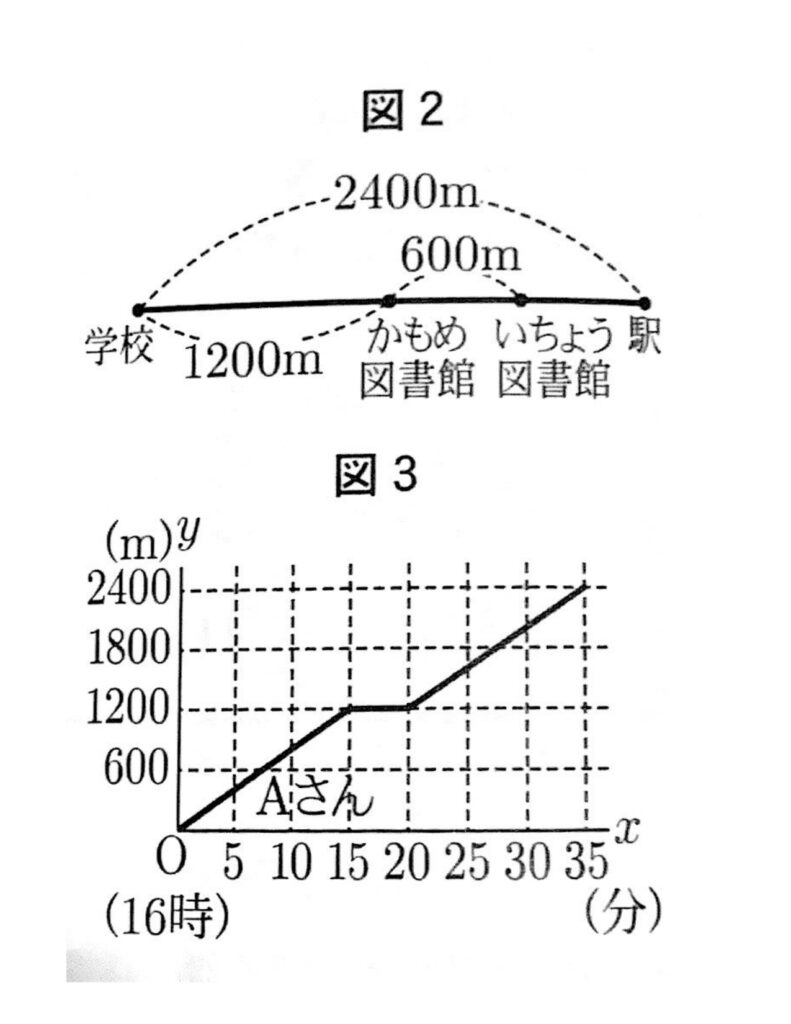
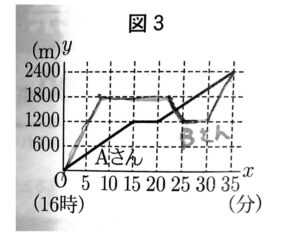
（ウ）学校から駅までの道のりは2400ｍであり、その途中にかもめ図書館といちょう図書館がある。AさんとBさんは16時に学校を出発し、それぞれが図書館に立ち寄ってから駅まで移動する中で一度すれ違ったが、駅には同時に到着した。
Aさんは、かもめ図書館に5分間立ち寄って本を借り、駅まで移動した。Bさんは、いちょう図書館に15分間立ち寄って借りたい本を探したが見つからなかったため道を引き返し、かもめ図書館に5分間立ち寄って本を借り、駅まで移動した。
次の図2は、学校、かもめ図書館、いちょう図書館、駅の間の道のりを示したものである。図3は、16時に学校を出発してからx分後の、学校からの道のりをymとして、Aさんが駅に到着するまでのxとyの関係をグラフに表したものであり、Oは原点である。
このとき、AさんとBさんがすれ違った時間帯として最も適するものをあとの1～6の中から1つ選び、その番号を答えなさい。ただし、AさんとBさんの、それぞれの移動中の速さは常に一定であり、図書館での移動は考えないものとする。
1：16時19分から16時21分までの間
2：16時21分から16時23分までの間
3：16時23分から16時25分までの間
4：16時25分から16時27分までの間
5：16時27分から16時29分までの間
6：16時29分から16時31分までの間
（エ）次の【 】の中の「う」「え」にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その番号を答えなさい。
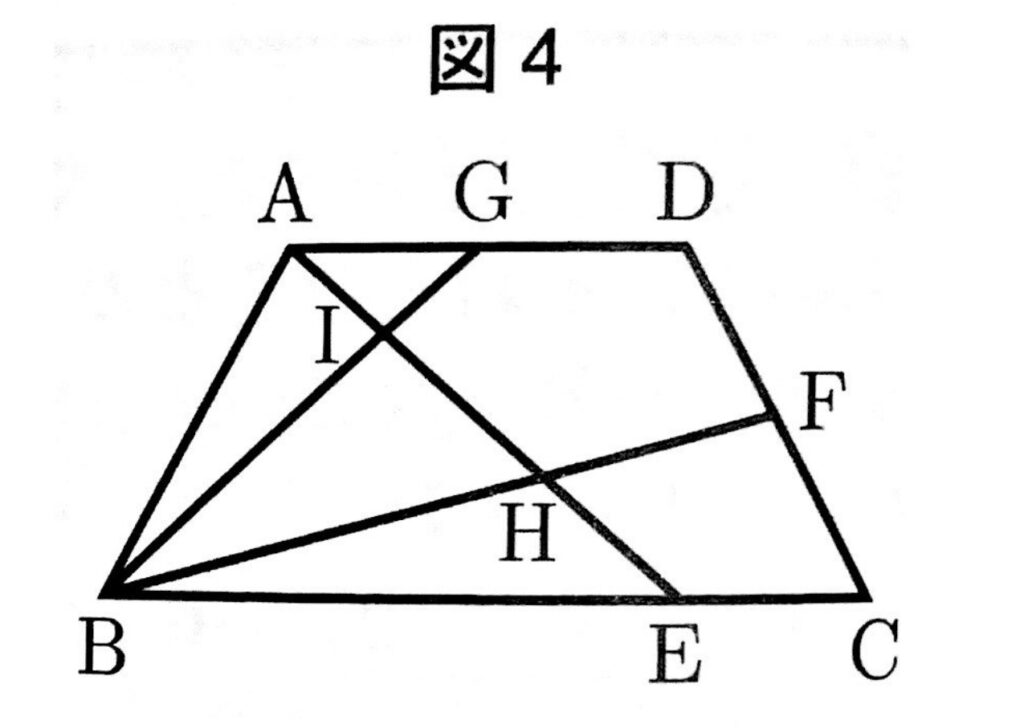
右の図4において、四角形ABCDはAB＝CD＝DA、AB:BC＝1：2の台形である。
また、点Eは辺BC上の点でBE:EC＝3：1であり、2点F,Gはそれぞれ辺CD,DAの中点である。
さらに、線分AEと線分BFとの交点をH,線分AEと線分BGとの交点をIとする。
三角形BHIの面積をS、四角形CFHEの面積をTとするとき、SとTの比を最も簡単な整数の比で表すとS:T＝【う】：【え】である。
解答・解説
（ア）（ⅰ）(a)3、(b)1、(c)4
(c)の選択肢の1は合同条件。
（ア）（ⅱ）36°
△ACBに注目すると、∠ACB＝90°（半円の円周角）、∠ABC＝∠AEC（円周角）＝∠BAI（相似）であることが分かるので、
∠ABCの大きさが分かれば、∠CAIの大きさは求まる。
∠ABCはDCを結ぶとできる三角形に注目すると
∠ABC＝180-（90+35+28）＝27°
よって、∠CAI＝180-（90+27+27）＝36°
※下図参照
（イ）（ⅰ）2
箱ひげ図を描くときは、最小値・最大値・中央値に注目すればよい。
最小値は13、最大値は25、中央値は18になるので、答えは2。
※中央値は偶数の場合真ん中の数二つの平均となり、$(17+19)\div2=18$
（イ）（ⅱ）6
A：最頻値は一番出てくる数字なので、$20$で正しい。
B：議案Yに賛成した総数は$(20+26+19+27+25+24+20+15+24+20)=220$、議案Zに賛成した総数は$23\times10=230$なので、誤り。
C：議案Yの中央値は$(20+24)\div2=22$となるので、正しい。
D：四分位範囲は第三四分位数から第一四分位数を引けば求まるので、議案Yの四分位範囲は$25-20=5$となるので、正しい。
（ウ）3
Bさんの駅に着くまでのグラフを図3に書き入れ、Aさんとの交点になる場所がすれ違った時間帯になる。
Bさんの速さを求めるために、Bさんが歩いていた時間を求める。Aさんと同時に駅に着いた（35分）と、立ち寄っていた時間（15分+5分）を考えると、歩いていた時間は$35-(15+5)=15分$である。
また、歩いた距離は一度かもめ図書館に戻っているので、$1800+600+1200=3600m$である。
これらよりBさんの移動速度は$3600m\div15分=240m/分$だと分かる。
すると、まずBさんがいちょう図書館までにかかった時間は$1800m\div240m/分=7.5分$
そこから、15分過ごしたので、いちょう図書館を出たのは$7.5分+15分=22.5分$
その後、かもめ図書館まで戻るのに要した時間は$600m/div240m/分=2.5分$
つまり25分経ったときにかもめ図書館についたことになる。
グラフを書いていくと、この途中でAさんとの交点があるので、答えは3となる。
（エ）5:4
AI:IH:HE＝3：5：4
辺BCの中点をMとし、△ABM＝Uとすると、
$S=U\times\frac{3}{2}\times\frac{5}{12}=\frac{5}{8}U$
$T=△BCF-△BEH=U-U\times\frac{3}{2}\times\frac{4}{12}=\frac{1}{2}U$
$S:T=\frac{5}{8}U:\frac{1}{2}U=5:4$
大問4 関数とグラフ
問題文
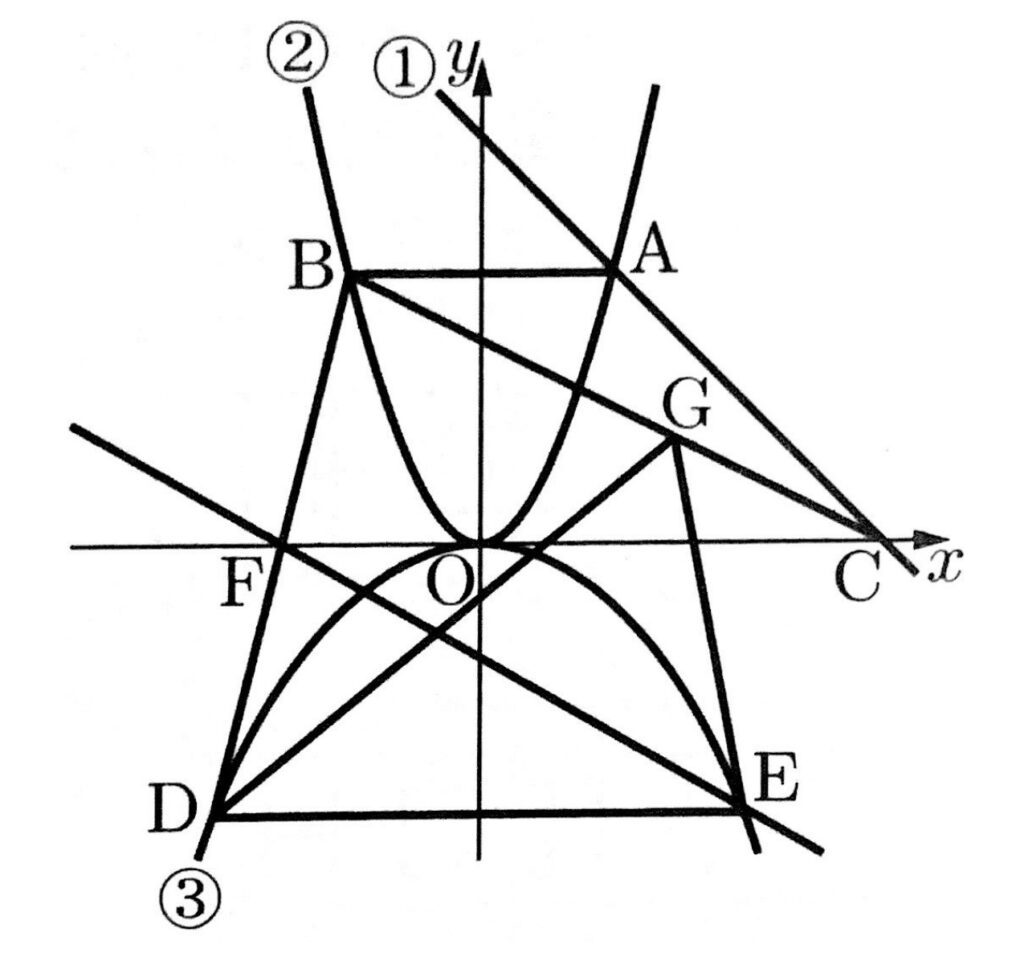
次の図において、直線①は関数$y=-x+9$のグラフであり、曲線②は関数$y=ax^2$のグラフ、曲線③は関数$y=-\frac{1}{6}x^2$のグラフである。
点Aは直線①と曲線②との交点で、そのx座標は3である。点Bは曲線②上の点で、線分ABはx軸に平行である。点Cは直線①とx軸との交点である。
また、2点D,Eは曲線③上の点で、点Dのx座標は-6であり、線分DEはx軸に平行である。
さらに、点Fは線分BDとx軸との交点である。
原点Oとするとき、次の問いに答えなさい。
（ア）曲線②の式$y=ax^2$のaの値として正しいものを次の1～6の中から1つ選び、その番号を答えなさい。
1：$a=\frac{1}{4}$ 2：$a=\frac{1}{3}$ 3：$a=\frac{2}{5}$
4：$a=\frac{1}{2}$ 5：$a=\frac{2}{3}$ 6：$a=\frac{3}{4}$
（イ）直線EFの式を$y=mx+n$とするときの(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1～6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1：$m=-\frac{5}{6}$ 2：$m=-\frac{5}{7}$ 3：$m=-\frac{2}{3}$
4：$m=-\frac{4}{7}$ 5：$m=-\frac{1}{3}$ 6：$m=-\frac{1}{6}$
(ⅱ)nの値
1：$n=-\frac{18}{7}$ 2：$n=-\frac{5}{2}$ 3：$n=-\frac{7}{3}$
4：$n=-\frac{13}{6}$ 5：$n=-\frac{15}{7}$ 6：$n=-2$
（ウ）次の【お】【か】【き】【く】にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その番号を答えなさい。
線分BC上に点Gを、三角形BDGと三角形DEGの面積が等しくなるようにとる。このときの、点Gのx座標は$\frac{【お】【か】}{【き】【く】}$である。
解答・解説
（ア）5
点Aの座標は①を通ることからA(3,6)である。
これを②に代入すればよいので、
$9a=6$
$a=\frac{2}{3}$
（イ）(ⅰ)4 (ⅱ)1
直線EFは2点E,Fの座標が分かれば求まる。
点Eは③上の点であり、E(6,-6)
直線BDの式が分かれば、点Fが求まる。
点B(-3,6)、点D(-6,-6)より、直線BDの式は$y=4x+18$となるので、点F($-\frac{2}{9}$,0)
よって、$m=-\frac{4}{7},n=-\frac{18}{7}$
（ウ）【お】5【か】7【き】1【く】3
線分BEの中点M($\frac{3}{2}$,0)であるから、直線DMの式は、$y=\frac{4}{5}x-\frac{6}{5}$
これと、直線BCの式$y=-\frac{1}{2}+\frac{9}{2}$を連立させて、$x=\frac{57}{13}$
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5 確率
問題文
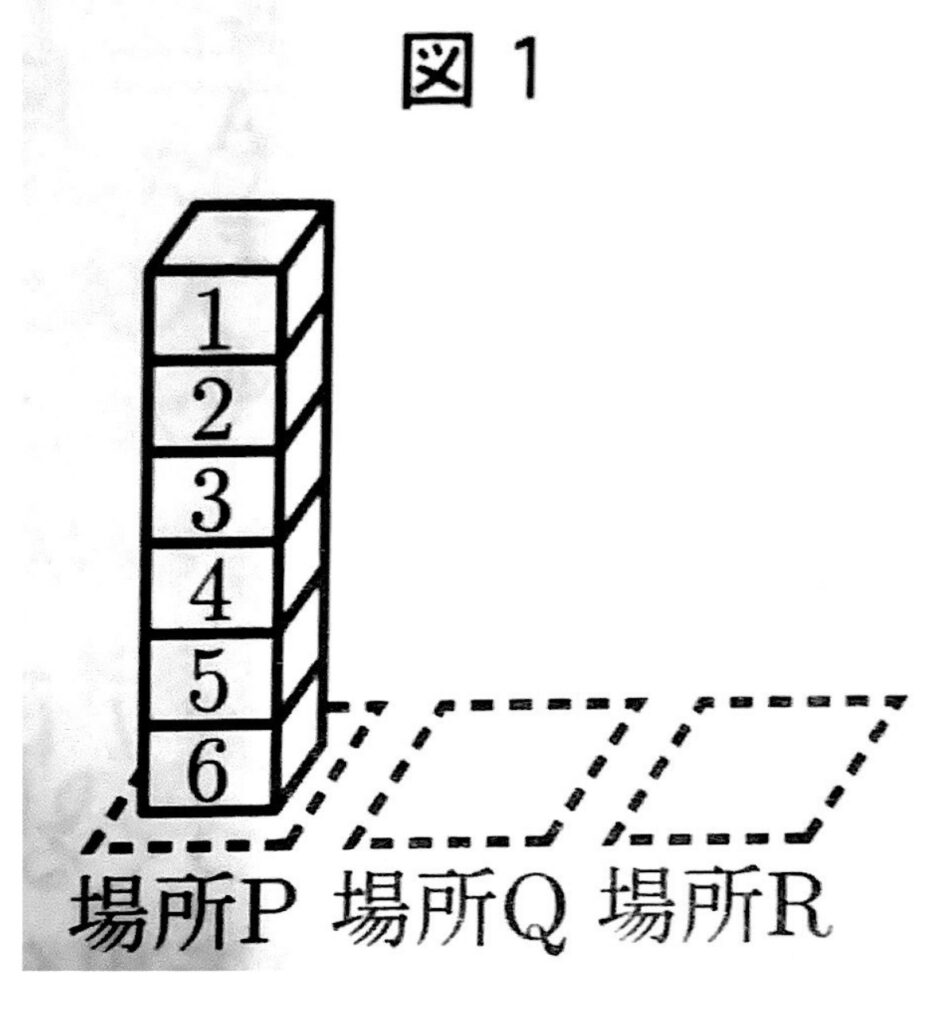
次の図1のように、場所P、場所Q、場所Rがあり、場所Pには、1，2，3，4，5，6の数が1つずつ書かれた6個の直方体のブロックが、書かれた数の大きいものから順に、下から上に向かって積まれている。
大、小2つのさいころを同時に1回投げ、大きいさいころの出た目の数をa、小さいさいころの出た目の数をbとする。出た目の数によって、次の【操作1】、【操作2】を順に行い、場所P、場所Q、場所Rの3か所にあるブロックの個数について考える。
【操作1】aと同じ数の書かれたブロックと、その上に積まれているすべてのブロックを、順番を変えずに場所Qへ移動する。
【操作2】bと同じ数の書かれたブロックと、その上に積まれているすべてのブロックを、bと同じ数の書かれたブロックが場所P、場所Qのどちらにある場合も、場所Rへ移動する。
例
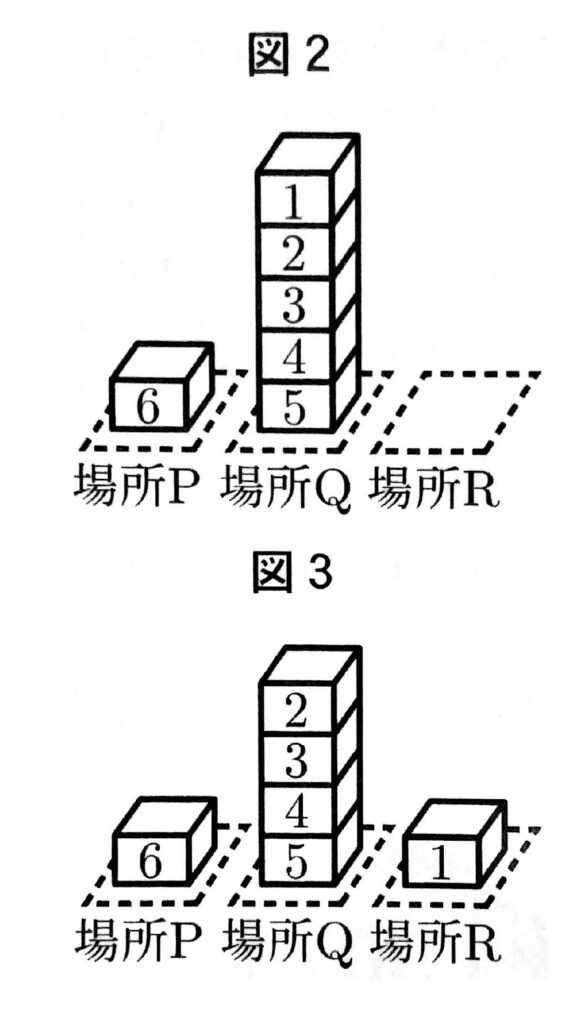
大きいさいころの出た目の数が5、小さいさいころの出た目の数が1のとき、a=5,b=1だから、
【操作1】図1の、5が書かれたブロックと、その上に積まれているすべてのブロックを、順番を変えずに場所Qに移動するので、図2のようになる。
【操作2】図2の、1が書かれたブロックを、場所Rへ移動するので、図3のようになる。
この結果、3か所にあるブロックの個数は、場所Pに1個、場所Qに4個、場所Rに1個となる。
いま、図1の状態で、大、小2つのさいころを同時に1回投げるとき、次の問いに答えなさい。ただし、大、小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。
（ア）次の【け】【こ】【さ】にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その数字を書きなさい。
ブロックの個数が3箇所とも同じになる確率は$\frac{【け】}{【こ】【さ】}$である。
（イ）次の【し】【す】にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その数字を答えなさい。
3か所のうち、少なくとも1か所のブロックの個数が0個になる確率は$\frac{【し】}{【す】}$である。
解答・解説
（ア）【け】1 【こ】1 【さ】8
全通りは$6\times6=36$通り。ブロックの個数が3箇所とも同じになるときはP,Q,Rとも2個ずつになるときである。
この時は、(a,b)=(2,4)(4,2)の2通りしかないので、$2\div36=\frac{1}{18}$
（イ）【し】4 【す】9
「少なくとも一つ」は「1」から「そうならない確率」をひけば求まる。
つまり、今回の場合は、「1」から「ブロックの個数が0にならない確率」を求めればよい。
ブロックの個数が0にならない確率は樹形図を書くと求まり、20通り。
よって、$1-\frac{20}{36}=\frac{4}{9}$
大問6 空間図形
問題文
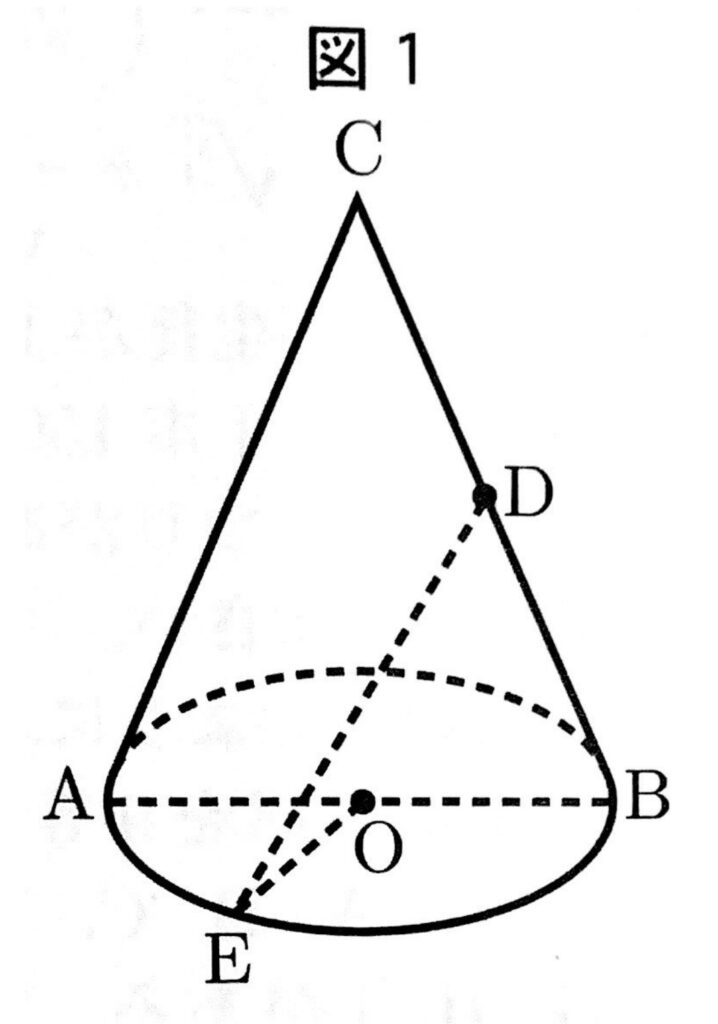
次の図1は、線分ABを直径とする円Oを底面とし、線分ACを母線とする円錐である。
また、点Dは線分BCの中点である。
さらに、点Eは円Oの周上の点である。
AB=8cm、AC=10cm、∠AOE＝60°のとき、次の問いに答えなさい。ただし、円周率はπとする。
（ア）この円錐の表面積として正しいものを次の1～6の中から1つ選び、その番号を答えなさい。
1：$24πcm^2$ 2：$28πcm^2$ 3：$40πcm^2$
4：$48πcm^2$ 5：$56πcm^2$ 6：$84πcm^2$
（イ）この円錐において、2点D,E間の距離として正しいものを次の1～6の中から1つ選び、その番号を答えなさい。
1：$\sqrt{43}cm$ 2：$7cm$ 3：$5\sqrt{2}cm$
4：$\sqrt{57}cm$ 5：$3\sqrt{7}cm$ 6：$8cm$
（ウ）次の【せ】【そ】にあてはまる数字をそれぞれ0～9の中から1つずつ選び、その数字を答えなさい。
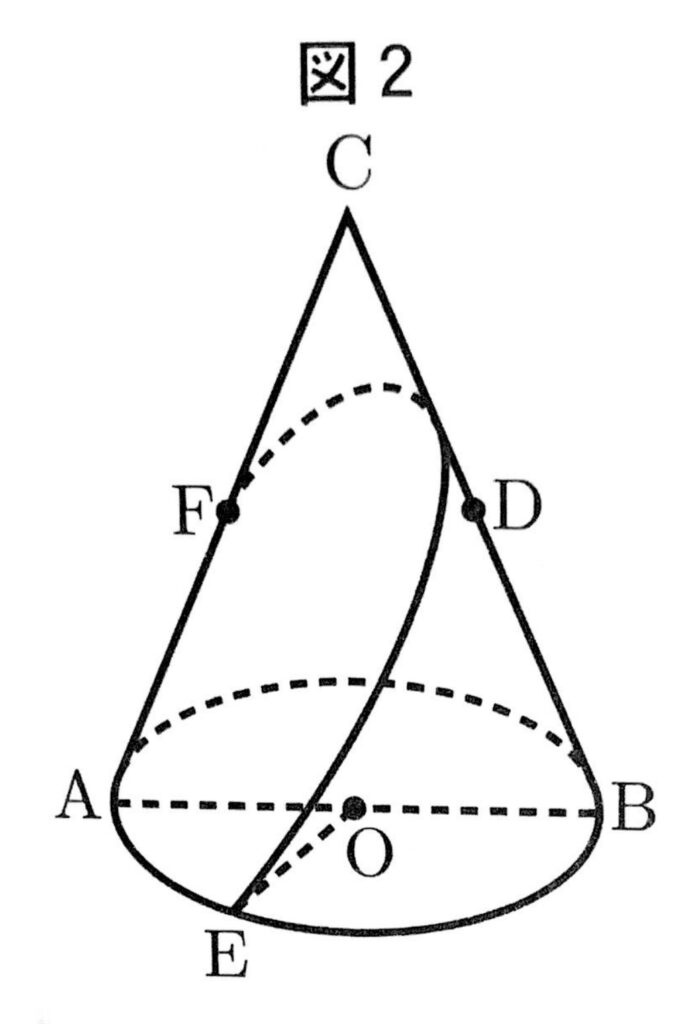
点Fが線分ACの中点であるとき、この円錐の側面上に、図2のように点Eから線分BCと交わるように、点Fまで線を引く。このような線のうち、長さが最も短くなるように引いた線の長さは$【せ】\sqrt{【そ】}cm$である。
解答・解説
（ア）5
表面積は底面積と側面積を求めればよい。
底面積：$4\times4\timesπ=16πcm^2$
側面積（直径×母線の長さ÷2）：$4\times2\timesπ\times10\div2=40πcm^2$
よって、$16πcm^2+40πcm^2=56πcm^2$
（イ）2
線分OBの中点をMとすると、∠EMD＝90°であるから、
三平方の定理を用いて、$DE=\sqrt{EM^2+DM^2}=\sqrt{(2\sqrt{7})^2+(\sqrt{21})^2}=7cm$
（ウ）【せ】5 【そ】7
展開図をかくと、CE=10cm、CF=5cm、∠ECF=120°
点Eから直線ACに垂線EHを引くとCH=5cm、
EH=$5\sqrt{3}$cmとなるので、求める長さは、
$\sqrt{FH^2+EH^2}=\sqrt{10^2+(5\sqrt{3})^2}=5\sqrt{7}cm$
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、神奈川県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
