【京都府】令和2年度/2020年度入学者高校入試選抜試験：数学の解説
京都府の2020年3月実施の令和2年度（2020年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
京都府の数学問題は、難易度としては難しい。小問集合と数列のような規則性を問う問題が必ず出るのが特徴です。
時間配分の仕方が肝になるので、時間を計りながら過去問に挑戦してみるといいかもしれません。
【京都府】令和2年度一般入学者選抜の過去問はこちらから
数学(前期)の過去問題はこちら＞＞
数学(中期)の過去問題はこちら＞＞
【前期】大問1：小問集合
問1：正負の数
問1：8×(-3/2)²-(-4²) を計算する問題です。
【・答え「34」】
与式=8×9/4-(-16)
=18+16=34
()内と外の2乗の外し方に注意。
問2：文字と式
問2：(4a-3)/6 -(6a-5)/9 を計算する問題です。
【・答え「1/18」】
与式={3(4a-3)-2(6a–5)/18}
=(12a-9-12a+10)/18=1/18
問3：多項式
問3：2/3x²y³÷(-1/8xy)÷4/9y を計算する問題です。
【・答え「-12xy」】
与式=2/3xy×(-8)×9/4＝-12xy
問4：平面図形
問4：半径4cm、面積6πcm²のおうぎ形の中心角の大きさを求める問題です。
【・答え「135°」】
半径4cmの円の面積=4×4×π＝16πcm²
おうぎ形の面積は6πcm²であるから
360×6π/16π=360×3/8=135°
問5：連立方程式
問5：連立方程式 ax-by=23，2x-ay=31 の解が x=5，y=-3 であるときのa，bの値を求める問題です。
【・答え「a=7，b=-4」】
x=5，y=-3をそれぞれの式に当てはめると、
5a+3b=23 …①，10+3a=31 …②
②より
10+3a=31
3a=31-10
a=7 …③
③を①へ代入
35+3b=23
3b=23-35
b=-4
問6：代入、平方根
問6：a=√30-6 のときの a²+12a+35 の値を求める問題です。
【・答え「29」】
与式=(a+7)(a+5)
上の式に a=√30-6 を代入すると
(√30-6+7)(√30-6+5)
=(√30+1)(√30-1)
=(√30)²-1²=30-1=29
問7：二次方程式
問7：二次方程式 3x²-8x-4=0 を解く問題です。
【・答え「x=(4±2√7)/3」】
二次方程式の解の公式を使って解く
問8：関数
問8：x＜0の範囲で、xの値が増加すると対応するyの値も増加する関数を選択肢(ア)～(カ)の中から選ぶ問題です。
【・答え「ア，ウ，カ」】
問9：確率
問9：白玉4個、黒玉2個の計6個が入った袋から2個の玉を取り出した時、黒玉が少なくとも1個は袋に残る確率を求める問題です。
【・答え「14/15」】
黒玉が2個しか入っていないことから、少なくとも1個残る=1-(2個とも黒) ということが言えます。
【前期】大問2：資料の整理
問1：中央値（選択問題）
問1：度数分布表から中央値として考えられるのもを5つの選択肢の中からすべて選ぶ問題です。
【・答え「ア，イ，ウ」】
1年生は50人なので、中央値は25人目と26人目の冊数の平均値です。
25人目も26人目も6冊以上8冊未満の階級なので、考えられるのは「2人とも6冊」「6冊と7冊」「2人とも7冊」です。
よって、考えられる中央値は6冊、6.5冊、7冊の3つ。
問2：度数（穴埋め問題）
問2：1年生の度数分布表、「1年生と3年生の4冊以上6冊未満の階級度数が等しいこと」「8冊以上10冊未満の階級度数は3年生の方が大きいこと」「3年生が図書館で借りた本の冊数の最大の値は16冊である」ことから3年生の度数分布表を穴埋めする問題です。
【・答え「X…8，Y…13，Z…1」】
4冊以上6冊未満の相対度数=10/50=1/5
x=40×1/5=8
1年生の8冊以上10冊未満の相対度数=15/50=3/10
「8冊以上10冊未満の階級度数は3年生の方が大きいこと」から
Y/40＞3/10 Y＞40×3/10 Y＞12
Y+Z=40-(8+2+6+4+6)=14
Y>12，Z≧1なので、Y=13，Z=1
【前期】大問3：平面図形
問1：証明
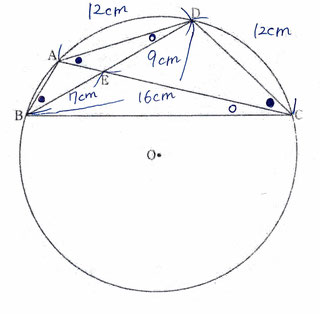
問1：△ABDと△EADが相似であることを証明する問題です。
【・答え
△ABDと△EADで、共通な角だから∠ADB=∠EDA …①
仮定より、△DACは二等辺三角形だから、∠ACD=∠EAD
弧ADに対する円周角等しいから、∠ACD=∠ABD
よって、 ∠ABD=∠EAD …②
①，②から、2組の角がそれぞれ等しいので△ABD∽△EAD 】
共通の角に気が付くことと、
二等辺三角形の底角が等しいこと、
弧に対する円周角は等しくなることがポイントです。
問2：比
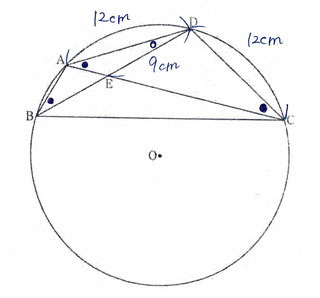
問2：比を使って線分BEの長さを求める問題です。
【・答え「7cm」】
問1より、△ABD∽△EADなので、
AD：ED=BD：AD
12：9=BE：12
9×BD=12×12
BD=16
BE=BD-ED
=16-9=7（cm）
問3：三平方の定理
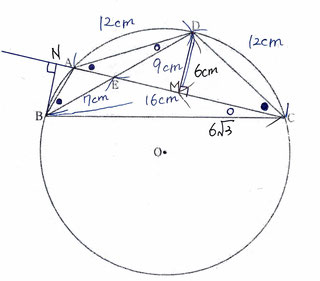
問3：∠ACD=30°のときの、線分ACの長さと△ABCの面積を求める問題です。
【・答え「AC=12√3，面積 28√3」】
＊線分AC
頂点DからACに向かって垂直な線を引くと、∠ACD=30°から
30°，60°，90°の直角三角形ができます。
上記の三角形の辺の比は 1：2：√3なので
DM：DC：MC=6：12：6√3になります。
DMはACの垂直二等分線なのでAC=2MC=6√3×2＝12√3 となります。
＊△ABCの面積
線分ACから頂点Aの方向に延長線を引いたうえで、頂点Bから直線ACに垂線を引きます。
△EBNと△EDMは相似なので、BN：DM=BE：DEとなり、数字を当てはめると、
BN：6=7：9 9BN=42 BN=14/3
よって△ABC＝AC×BN×1/2=12√3×6×1/2=28√3となります。
【前期】大問4：関数
問1：
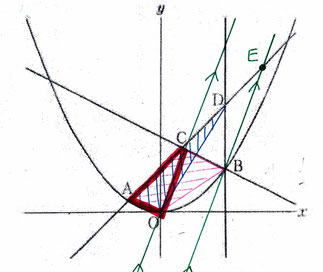
問1：2次関数y=ax²のaの値と、点Aのx座標を求める問題です。
【・答え「a=1/9，x=-3」】
＊aの値
点Bは直線y=-1/2x+7を通るx座標が6の点なので
y=-1/2×6+7=4
よってBの座標は(6，4)
y=ax²は点Bを通るので
4=a×6²
a=1/9
＊点Aのx座標
AC：CD=5：4なのでx座標の差の比を考えると
(2-x)：(6-2)=5：4 なので、x=-3
問2：
問2：座標から直線ACの式を求める問題です。
【・答え「y=x+4」】
問1から、点Aのx座標は-3であり、点Aはy=1/9x²上の点なので
y=1/9×(-3)²=1
よって、直線ACの傾きは1となります。
点Cのx座標は2で、直線y=-1/2x+7上の点なので
点Cのy座標はy=-1/2×2+7=6 となるため点Cの座標は(2，6)になります。
点Cを通る傾きが1の直線は、6=1×2+b からb=4なので、y=x+4 となります。
問3：
問3：直線AC上にある四角形OBCAと△OEAの面積が等しくなる点Eを求める問題です。
【・答え「E(9，13)」】
四角形OBCA（ピンクの部分）と△OEA（青の部分）はどちらも△OAC（赤の部分）を含む図形です。
したがって、△OBCと△OECの面積が等しくなれば四角形OBCAと△OEAは等しくなります。
線分OCを底辺とすると、底辺が共通で高さが同じなら面積も同じになるので点Bを通り、直線OCに平行な直線と直線ACとの交点がEになります。
直線OCは原点と点C(2，6)を通るのでy=3x
この直線と平行で、点Bを通る直線は 4=3×6+b b=-14だから y=3x-14です。
直線y=3x-14と直線ACの交点は連立方程式 y=3x-14，y=x+4 解くとx=9，y=13となるため、点Eは(9，13)になります。
【前期】大問5：空間図形
問1：三平方の定理
問4：線分PQの長さを求める問題です。
【・答え「6√2cm」】
PQ=BDであり、四角形ABCDは一辺が6cmの正方形なので三平方の定理からPQ=6√2になります。
問2：ひし形
問2：四角形CQRPの面積と、直線CQと直線PRの距離を求める問題です。
【・答え「四角形CQRP…18√6cm²，距離…6/5√30cm」】
＊面積
条件より、AC=6√2、AR=6
三平方の定理より、CR²=(6√2)²+6²
よって、CR=6√3
四角形CQRPを取り出すと、ひし形ということがわかります。
したがって、四角形CQRPの面積は1/2×6√2×6√3=18√6(cm²)となります。
＊距離
ひし形の1辺の長さは√（6²+3²）=3√5です。
直線CQと直線PRの距離は点Rから直線CQに引いた垂線l（つまり高さ）であり、四角形CQRPの面積は18√6なので、18√6=3√5×l よって、l=6/5√30（cm）
問3：体積（三角錐）
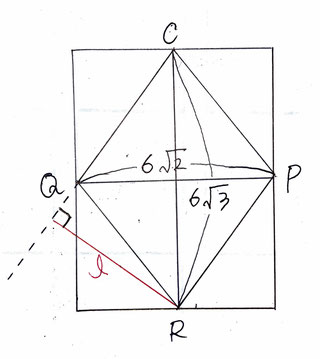
問3：三角錐MCQPの体積を求める問題です。
【・答え】三角錐MCQP=27㎤
MS=FMより、三角錐MCQPの体積は三角錐FCQPの1/2になる。
三角錐FCAPの面積は底辺CPF×高さCD×1/3より、
FCPQ＝1/2×9×6×6×1/3＝54㎤
MCQP=1/2×FCPQより、MCQP=27(㎤)
【前期】大問6：文字と式（規則性）
問1：穴埋め問題
問1：問題文の文中の空欄に当てはまる数字を規則性から計算して求める問題です。
【・答え「ア…18，イ…24」】
＊ア
［6］の箱に玉を入れるのはnが6の倍数のときだけです。
よって、［6］の箱に3個目の玉を入れるのは 6×3=18（回目）となります。
＊イ
同じく、4つ目は 6×4=24（回目）です。
問2：
問2：規則性をつかんで、aとbの値を求める問題です。
【・答え「a…51，b=17」】
問1より、（回数）=（箱の数字）×（箱の中の個数）であることがわかるので、
［3］の箱にb個目の玉を入れるのは a=3b …①
そこから85回目操作で［8］の箱にb個目の玉を入るので、n=3b+85となり
［8］の箱にb個目の玉を入れるのは n=8bのときなので、 3b+85=8b …②
①と②より a=51，b=17 となります。
問3：
問3：267回目の操作から赤玉のかわりに黄玉を使って操作を続けた場合、［4］の箱に入っている赤玉の数と［9］の箱に入っている黄玉の数が等しくなるときの［4］の箱に入っている黄玉の個数を求める問題です。
【・答え「147個」】
問1、問2と同じようにnまでに箱に書かれた数字の倍数が何回出てくるかがわかると玉の数が求められます。
267回目から赤玉から黄玉になるので、266回目の時点で
［4］の箱は 266=4×66+2 ［9］の箱は 266=9×29+5 で
4の倍数は66回、9の倍数29回出てくるので
赤玉は［4］の箱に66個、［9］の箱に29個はいいていることになります。
この後に［9］の箱に黄玉が66個入るのは、29+66で95個になったときなので、
n=9×95=855（回目）の操作ということになります。
855回目の時点で、［4］の箱は
855=4×213+3で 213個の玉が入っていることになります。
213個のうち66個は赤玉なので、黄玉は 213-66=147（個）となります。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
【中期】大問1：小問集合
問1：正負の数
問4：5+4×(-3²) を計算する問題です。
【・答え「-31」】
与式=5+4×(-9)
=5-36=-31
()内の2乗の外し方に注意。
問2：文字と式
問5：4(3x+y)-6(5/6ｘ-4/3y) の計算をする問題です。
【・答え「7x+12y」】
与式=12x+4y-5x+8y
=7x+12y
問3：平方根
問3：√3×√32+3√6 の計算をする問題です。
【・答え「7√6」】
与式=√3×4√2+3√6
=4√6+3√6=7√6
問4：連立方程式
問4：連立方程式 2x+5y=-7，3x+7y=-9 を計算する問題です。
【・答え「x=4，y=-3」】
2x+5y=-7 …①，3x+7y=-9 …② とする。
①×3-②×2を計算すると
y=-3 …③とする。
③を①へ代入すると
2x+5×(-3)=-7
2x=8
x=4
問5：一次関数
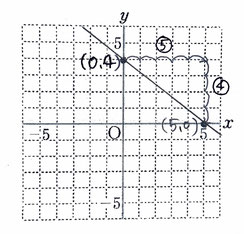
問5：y=-4/5x+4 のグラフを描く問題です。
【・答え「下記のグラフを参照」】
①グラフの切片は「+4」なので、y軸上の(0，4)の座標に点をとる。
②傾きが-4/5なので、①の点からx軸方向に+5、y軸方向に-4の(5，0)の座標に点をとる。
③2点を通る直線を引く。
問6：平方根
問6：5＜√n＜6 をみたす自然数nの個数を求める問題です。
【・答え「10個」】
5と6をそれぞれ平方根に直すと√25と√36になる。
25と36を含まない、2つの間の自然数は26，27…，35の計10個。
整数を平方根にする方法と、不等号の読み方に注意。
問7：平面図形（円周角）
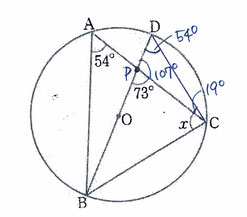
問7：図から、∠xの角度を求める問題です。
【・答え「∠ｘ=71°」】
1つの弧(弧BC)からなる円周角は等しいので、∠BDC=54°
直線ACと直線BDの交点をPとすると、∠CPD=180°-73°=107°
∠PCD=180°-(107°+54°)=19°
直径を通る三角形の円周角は必ず90°であるから∠x=90°-19°=71°
問8：方程式（比例式）
問8：10000個の製品から無作為に取り出した300個の製品から7個の不良品が見つかったことから、10000個の製品中に含まれる不良品のおよその数を求める問題です。
【・答え「およそ230個」】
x：7=10000：300
300x=70000
x=70000÷300≒233.… 一の位を四捨五入すると230個
【中期】大問2：確率
問1：
問1：さいころを2回投げて、積み木を移動させる操作における確率を求める問題です。操作を2回続けて行うとき、Gの積み木が一番上になる確率を求めます。
【・答え「1/6」】
さいころの目は6までしかないので、1回目でどの数が出たとしてもGは1つ下がって上から2番目になります。
2回目で上から2番目の積み木が一番上になるには2回目で6が出なければなりません。
1回目→1～6どれでも（6通り）
2回目→6のみ（1通り）なので6×1=6
さいころを2回投げるときは36通りの出方があるので6/36=1/6
問2：
問2：さいころを2回投げて、積み木を移動させる操作における確率を求める問題です。操作を2回続けて行うとき、下から4番目の積み木がEの積み木になる確率を求めます。
【・答え「1/3」】
Eはもともと下から5番目の積み木なので、下から4番目にくるためには、1つ下がる必要があります。
1回目で一番上にくると、さいころの目は6までしかないので2回目で動きません。
よって、まず1回目に5が出た場合は除かれます。
1回目で1つ下がって、2回目では動かないのは
1回目で1～4、なおかつ2回目で5か6が出た場合なので4×2=8（通り）。
1回目では動かず、2回目で1つ下がるのは
1回目で6、2回目で1～4が出た場合なので4通り。
8+4=12（通り）で、
さいころを2回投げるときは36通りの出方があるので12/36=1/3
【中期】大問3：関数
問1：
問1：1往復するのにかかる時間をx秒、振り子の長さymとしたときにy=1/4x²の関係が成り立つとき、1往復2秒かかる振り子の長さと、長さが9mの振り子が1往復するのにかかる時間を求める問題です。
【・答え「長さ…1m，時間…6秒」】
＊長さ
「1往復するのに2秒かかる」→ x=2
このとき y=1/4×2²=1（m）
＊時間
「振り子の長さが9m」→ y=9
このとき 9=1/4x² x=±6
xは時間（秒）だからｘ＞0なので x=6
問2：
問2：振り子Aと振り子Bがあり、2つの振り子の関係から振り子Aの長さを求める問題です。
【・答え「25/36m」】
「振り子Aの長さはBより1/4長い」「振り子Bの1往復する時間はAの4/5倍である」
振り子Aの長さをl、1往復すのにかかる時間をsとすると
振り子Aは l=1/4s² …①
振り子Bは条件から l-1/4=1/4（4/5s）² …②
長さを求めればよいので、sを消して、lについて求める式にします。
①より 4l=s² …①´ ②より l-1/4=4/25s² …②´
①´を②´に代入すると
l-1/4=16/25l
9/25l=1/4 l=1/4×25/9 l=25/36（m）になります。
【中期】大問4：空間図形
問1：
問1：点Pが頂点Aから頂点Cに到達するのにかかる時間を求める問題です。
【・答え「8秒」】
点Pは毎秒1cmずつ動くことから
「点Pが頂点Aから頂点Cに到達する時間」=「辺ACの長さ」と言えます。
AC=√AB²+BC²
=√(2√7)²+6²=√64=±8 AC＞0なので 8（秒）となります。
問2：
問2：△BCDの面積、三角錐ABCDの体積を求める問題です。
【・答え「面積…√35，体積…14√5/3」】
＊面積
BC=BDであることから、△BCDは二等辺三角形ということが言えます。
よって、頂点BからCDに向かって垂直二等分線を引くと△BCDの高さを求めることができます。
垂直二等分線とCDの交点をMとすると
BM=√6²-1²=√35
したがって、 1/2×2×√35=√35（cm²）
＊体積
三角錐ABCDは、△BCDを底面、ABを高さとする立体なので、
1/3×√35×2√7=14√5/3（cm³）
問3：
問3：点Qが、頂点Aを点Pと同時に出発し、辺AB上を頂点Bに向かってBC//QPが成り立つように進むとき、三角錐AQPDの体積が24√5/7cmとなるのは点Pが頂点Aを出発してから何秒後か求める問題です。
【・答え「48/7秒後」】
【中期】大問5：平面図形
問1：
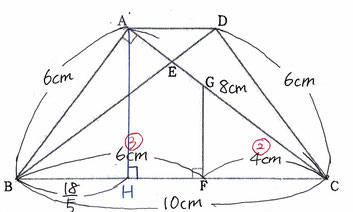
問1：点Aと辺BCとの距離、辺ADの長さを求める問題です。
【・答え「距離…24/5cm，AD=14/5」】
＊距離
「点Aと辺BCの距離」=△ABCの底辺をBCと見たときの「高さ」です。
△ABCをABを底辺とみると、面積は6×8×1/2=24（cm²）
また、三平方の定理から BC=√6²+8²=10（cm）なので
点AからBCに引いた垂線とBCの交点をHとすると
1/2×10×AH=24 AH=24/5（cm）となります。
＊ADの長さ
点DからBCに引いた垂線とBCの交点をIとすると
△ABH=△DCIになります。
三平方の定理からBH²=√AB²-AH²=6²-(24/5)²=18²/5² よってAH=CI=18/5 なので
AD=BC-(BH+CI)=10-36/5=14/5（cm）となります。
問2：
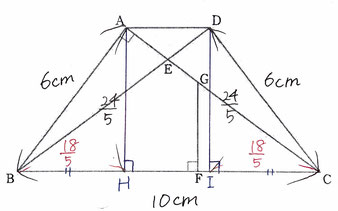
問2：AG：GCを求め、最も簡単な整数で表す問題です。
【・答え「3：5」】
BF：FC=3：2なので、CF=4
また、CH=BC-BH=10-18/5=32/5 となり、
このとき、HF=CH-CF=32/5-4=12/5 となります。
また、AH//GFなので、AG：GC=HF：FC
=12/5：4=12：20=3：5 になります。
問3：
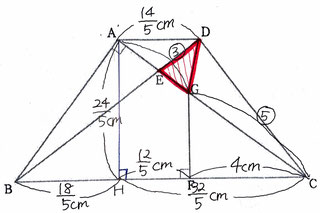
問3：△DEGの面積を求める問題です。
【・答え「21/20cm²」】
△ACD=1/2×AD×AH=1/2×14/5×24/5=168/25（cm²）
△AED∽△CEBなので
AE：CB=AD：CB=14/5：10=7：25
よって AE：EC=7：25 …①，問2よりAG：GC=3：5 …②
ACを32とすると、①，②よりEGは5/32となる。
したがって△DEG=168/25×5/32=21/20（cm²）となります。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
