京都府の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 京都府の公立高校入試情報はこちら

大問1

問題文

(1) -6²+4÷(-2/3)を計算せよ。

(2) 4ab²÷6a²b×3abを計算せよ。

(3) √48-3√2×√24を計算せよ。

(4) 次の連立方程式を解け。
4x+3y=-7
3x+4y=-14

(5) x=√5＋3，y=√5-3のとき、xy²-x²yの値を求めよ。

(6) 関数y=16/xのグラフ錠にあり、x座標、y座標がともに整数となる点の個数を求めよ。

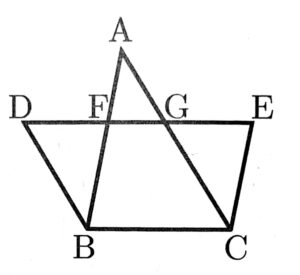
(7) 右の図において，AB//EC，AC//DB，DE//BCである。また，線分DEと線分AB，ACとの交点をそれぞれF，Gとすると，AF:FB=2:3であった。
BC=10 cmのとき線分DEの長さを求めよ。

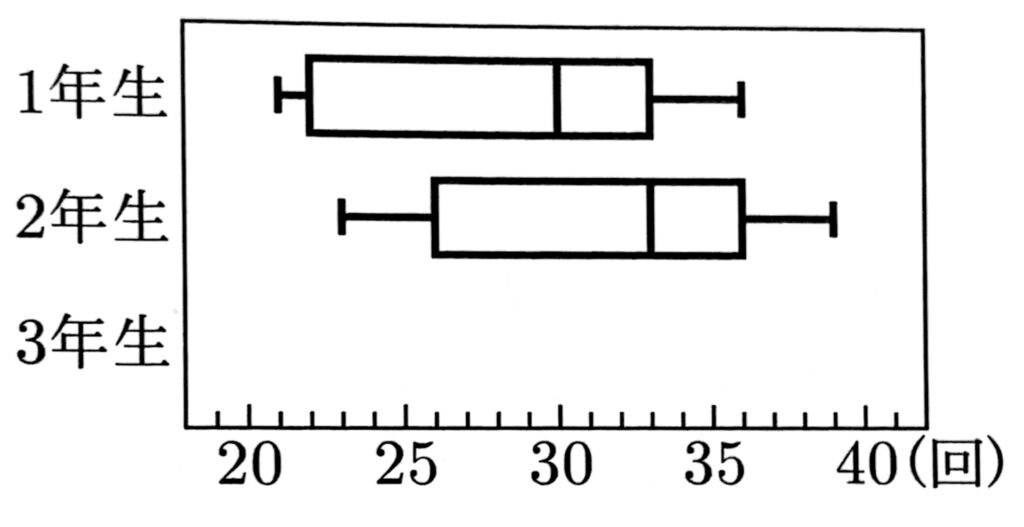
(8) 3学年がそれぞれ8クラスで編成された，ある中学校の体育の授業で，長なわ跳びを行った。右上の図は，各クラスが連続で跳んだ回数の最高記録を学年ごとに箱ひげ図で表そうとしている途中のものであり，1年生と2年生の箱ひげ図はすでにかき終えている。また，下の資料は，3年生のクラスごとの最高記録をまとめたものである。図の1年生と2年生の箱ひげ図を参考にし，あとの図に3年生の箱ひげ図をかき入れて，図を完成させよ。

解答・解説

（1）たし算割り算よりも掛け算割り算を先に計算する。また二乗は「6」だけにかかっているのに注意する
（与式）=-36-6=-42

（2）割り算は逆数の掛け算にして計算をすると解きやすい。
（与式）=2b2

（3）ルートは二乗で外に出すことができる。
（与式）=4√3-3√2×2√6=4√3-12√3=-8√3

（4）加減法で解けばよい
x=2,y=-5

（5）先に因数分解をすると計算が楽になる。
（与式）=xy(y-x)=(√5＋3)(√5-3){(√5-3)-(√5＋3)}
=(5-9)(-6)=24

（6）変形するとxy=16となるので、積が16となるx,yのペアを求めればよい。
(x,y)=(1,16)(2,8)(4,4)(8,2)(16,1)(-1,-16)(-2,-8)(-4,-4)(-8,-2)(-16,-1)の10個

（7）△ABCに注目するとAF:AB＝FG:BCが成立することが分かる。
よって、2:5=FG:10cm⇒FG=4cmが求まる。
次に△AFGと△BFDに注目すると相似であることが分かるので、AF:BF=FG:FDが成立する。
よって、2:3=4cm:FD⇒FD=6cmが求まる。
最後に四角形FBCEに注目すると、この四角形は平行四辺形であると分かる。性質として対辺の長さが等しいのでFE=BC=10cm
これらより、DE=FD+FE=16cm

（8）最小値24，第一四分位数28、中央値32、第三四分位数37、最大値40となるグラフを書けばよい。

大問2

問題文

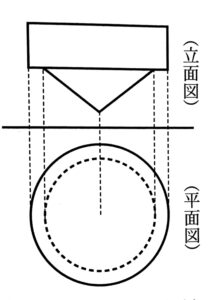
底面の半径が5cmの円柱と，底面の半径が4cmの円籍があり，いずれも高さは3cm である。この2つの立体の底面の中心を重ねてできた立体をXとすると，立体Xの投影図は右の図のように表される。
このとき，次の問い(1)・(2)に答えよ。

(1) 立体Xの体積を求めよ。

(2) 立体Xの表面積を求めよ。

解答・解説

（1）立体の体積は単純に足し合わせばよいので、
円柱の体積：5×5×π×3=75π
円錐の体積：4×4×π×3÷3=16π
よって、91πcm3

（2）表面積はくっついている部分の面積だけ気を付ける。具体的には円柱の底面積から円錐の底面積を引けば出るので
円柱の底面積＋円柱の側面積＋くっついてる部分の面積＋円錐の側面積で求まる。
（5×5×π）＋（10π×3）＋｛（5×5×π）-（4×4×π）｝＋｛5×5×π×(2×4×π)/(2×5×π)｝
=25π+30π+9π+20π=84πcm2

大問3

問題文

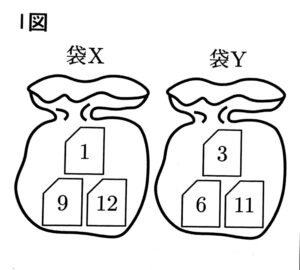
Ⅰ図のように，袋Xと袋Yには，数が1つ書かれたカードがそれぞれ3 枚ずつ入ってい る。 袋Xに入ってい るカードに書かれた数はそれぞれ1，9，12であり，袋Yに入って いるカードに書かれた数は それぞれ3，6，11 である。
真人さんは袋Xの中から，有里さんは袋Yの中からそれぞれ 1 枚のカードを同時に取り出し， 取り出したカードに書かれた数の大きい方を勝ちとするゲームを行う。
このとき，次の問い(1)・(2)に答えよ。ただし，それぞれの袋において，どのカードが取り出されることも同様に確からしいものとする。

(1) 真人さんが勝つ確率を求めよ。

(2) Ⅱ図のように，新たに数が1つ書かれたカードを7枚用意した。 これらのカードに書かれた数はそれぞれ2, 4, 5, 7, 8, 10, 13 である。4と書かれたカードを袋 X に， 2, 5, 7, 8, 10, 13と書かれたカードのうち，いずれか1枚を袋Yに追加してゲームを行う。
このとき真人さんと有里さんのそれぞれの勝つ確率が等しくなるのは，袋Yにどのカードを追加したときか，次の(ア)～(カ)からすべて選べ。

解答・解説

（1）起こり得るパターンは
（1，3）（1，6）（1，11）（9，3）（9，6）（9，11）（12，3）（12，6）（12，11）の9パターン、そのうち真人さんが勝つのは、5パターンなので
5/9が答えとなる

（2）1枚ずつ増やすことによって、全通りのパターンは16パターンとなる。確率を等しくするためには8パターンの勝つ通りを作らなければならない。（1）の時点で5パターン存在しており、4をXに入れることで、1パターン勝つことが確定するので、残り2パターン勝つ組み合わせを作るためには、イウエの5，7，8をいれればよいと分かる。

大問4

問題文

図のような，1辺が6cmの正方形ABCDがある。点Pは，頂点Aを出発し，辺AD上を毎秒1cmの速さで 頂点Dまで進んで止まり，以後，動かない。また，点Qは，点P が頂点Aを出発するのと同時に頂点Dを出発し，毎秒1cmの速さで正方形ABCDの辺上を頂点C,頂点Bの順に通って頂点Aまで進んで止まり，以後動かない。
点Pが頂点Aを出発してから，x秒後の△AQPの面積をy㎠とする。

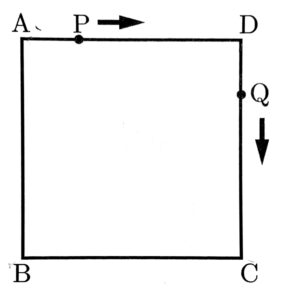
このとき，次の問い(1)・(2)に答えよ。

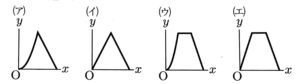
(1) x=1のとき，yの値を求めよ。また，点Qが頂点Dを出発してから，頂点Aに到着するまでのxとyの関係を表すグラフとして最も適当なものを，次の(ア)～(エ)から1つ選べ。

(2) 正方形ABCDの対角線の交点をRとする。
0≦x≦18において，△RQDの面積が△AQPの面積 と等しくなるような，xの値をすべて求めよ。

解答・解説

（1）x=1の時は、底辺1ｃｍ、高さ1ｃｍの三角形になるので、面積は1/2㎠となる。
0≦x<6の時、y=1/2×2
6≦x<12の時、y=18
12≦x≦18の時、y=54-3x
となるので、グラフはウが適当。

（2）△RQDの面積をzとすると、
0≦x<6の時、z=3/2x
6≦x<12の時、z=-3/2x+18
12≦x≦18の時、z=3/2x-18
となる。面積が等しくなるためにはy=zとなるxが変域を満たすかを考えればよいので、
x=3,16

大問5

問題文

図のように，円0の周上に5点A，B， C，D，Eがこの順にあり，線分ACと線分 BEは円0の直径である。また， AE=4cmで，∠ABE=30°，∠ACD=45°である。線分ADと線分BEとの交点をFとする。

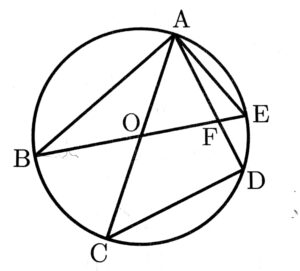
このとき次の問い(1)～(3)に答えよ。

(1) 円Oの直径を求めよ。

(2) 線分EFの長さを求めよ。

(3) 線分ACと線分BDとの交点をGとするとき，△OBGの面積を求めよ。

解答・解説

（1）三角形ABEに注目すると、AE:BE=1:2となるので、BE＝8ｃｍ

（2）円周角の定理より、∠AOE＝60°であり、△AOEが正三角形だと分かる。
ここから、EF＝OE-OFで求まると筋道を立てる。OE=4ｃｍなので、ＯＦを求めてみる。
点ＦからＡＯに垂線を下ろし、交点をＨとする。三平方で求めるのは常套手段なので、覚えておこう。
すると、△ＯＨＦに注目すると、OH:OF=1:2であり、OF=2OH
OHを求めるために、OH+HA=OAに注目すると、HAを求めれば良いと分かる。
∠CAD＝45°なので、△HAFは直角二等辺三角形であり、HA＝HFである。さらに、HF＝√3OHなので、OH+HA=OA⇒OH+√3OH＝4⇒OH＝2（√3-1）
よって、EF＝OE-OF＝4-2OH＝4-4（√3-1）＝8-4√3ｃｍ

（3）△OBGでは求め辛いので、合同な三角形を探すと、△EAFが見つかる。
△EAF＝△AOE×EF/OEで求まる。
△AOEは1/2△ABEなので、1/2×（1/2×4×4√3）＝4√3㎠
よって、△EAF＝4√3×（8-4√3）/4＝8√3-12㎠

大問6

問題文

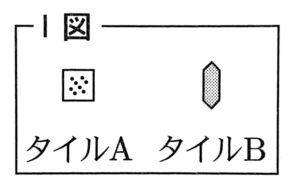
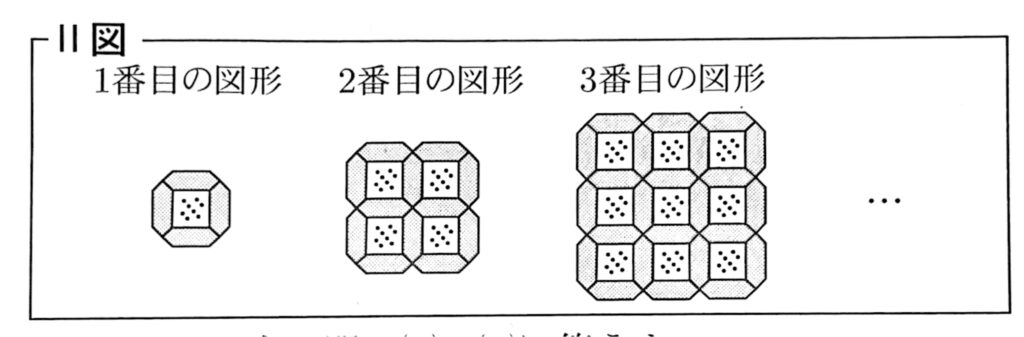
Ⅰ図のような，タイルAとタイルBが，それぞれたくさんある。タイルAとタイルBを，次のⅡ図のように，すき間なく規則IタイルAタイルB的に並べたものを，1番目の図形，2番目の図形，3番目の図形，・・・とする。

たとえば，2番目の図形において，タイルAは4枚，タ イルBは12枚である。

このとき，次の問い(1)～(3)に答えよ。

(1) 5番目の図形について，タイルAの枚数を求めよ。

(2) 12番目の図形について，タイルBの枚数を求めよ。

(3) n番目の図形のタイルAの枚数とタイルBの枚数の差が360枚であるとき，nの値を求めよ。

解答・解説

１番目の図形がタイルA：１枚、タイルB：4枚、2番目の図形がタイルA：4枚、タイルB：12枚、3番目の図形がタイルA：9枚、タイルB：24枚
ということから、タイルAは1，4，9，16【12,22,32,42…】と増えていき、タイルBは4,12,24,40【（1×2×2）、（2×3×2）、（3×4×2）、（4×5×2）】と増えていくので、
（1）25枚
（2）312枚
（3）n番目とすると、タイルAはn2、タイルBはn(n+1)×2=2n2+2n
差が360となるので、（2n2+2n）-n2＝360これを解いて、n=18

 京都府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。