三重県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 三重県の公立高校入試情報はこちら

大問1

問題文

⑴ 8 × (-7) を計算しなさい。

⑵ 4/5x – 2/3x を計算しなさい。

⑶ 15xy ÷ 5x を計算しなさい。

⑷ 5(2a+b) – 2(3a+4b) を計算しなさい。

⑸ (√3 + 2√7) (2√3 – √7) を計算しなさい。

⑹ yはxに反比例し、グラフが点(-2 , 8)を通る。yをxの式で表しなさい。

⑺ 二次方程式 2x² + 5x – 2 ₌ 0 を解きなさい。

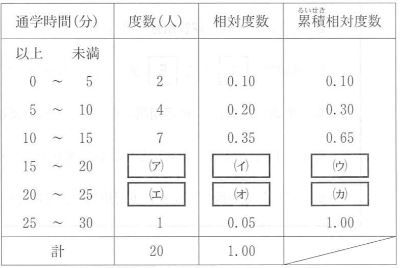
⑻ 表は、あるクラス20人の通学時間をまとめたものである。［　(ウ)　］にあてはまる数が0.80以下のとき、[　(ア)　]にあてはまる数をすべて求めなさい。

解答・解説

(1) -56
8 × (-7) ₌ -56

(2) 2/15x
4/5x – 2/3x ₌ 12/15x – 10/15x ₌ 2/15x

(3) 3y
15xy ÷ 5x ₌ 15xy/5x ₌ 3y

(4) 4a – 3b
5(2a + b) – 2(3a + 4b) ₌ 10a + 5b – 6a – 8b ₌ 4a – 3b

(5) – 8 + 3√21
(√3 + 2√7) (2√3 – √7) ₌ (√3 × 2√3) × (√3 × (-√7)) + (2√7 × (-7)) ₌ 6 – √21 + 4√21 – 14 ₌ – 8 + 3√21

(6) y ₌ -16/x
反比例の式は y ₌ a/x なので、8 ₌ -a/2 より a ₌ -16 となる。よって y ₌ -16/x

(7) (-5 ± √41)/4
解の公式 x ₌ (-b ± √b² – 4ac)/2a に数を入れる。
x ₌ (-5 ± √5² – 4 × 2 × (-2))/(2 × 2) ₌ (-5 ± √25 + 16) ₌ (-5 ± √41)/4

(8) 0,1,2,3
(ウ)に入る最も小さい数は0.65で最も大きい数は0.80
(ウ)が0.65のとき、(10～15分)の累積相対度数から変化が無いため度数(ア)は0となる。
(ウ)が0.80のとき、累積度数は 20人×0.80 ₌ 16人 と分かるため
度数(ア)は 16 – (2 + 4 + 7) ₌ 3 となる。よって (ア)に入る数は 0,1,2,3 となる。

大問2

問題文

⑴ まなぶさんは、A組 19人とB組 18人のハンドボール投げの記録について、ノートにまとめている。下の〈まなぶさんがまとめたノートの一部〉の図1は、B組全員のハンドボール投げの記録を記録が小さい方から順に並べたもの、図2は、A組全員のハンドボール投げの記録を箱ひげ図にまとめたものである。
このとき、次の各問いに答えなさい。

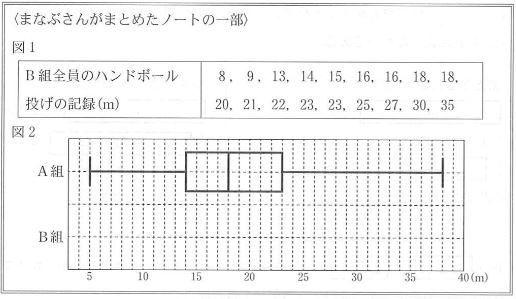
① B組全員のハンドボール投げの記録の中央値を求めなさい。

② 図1をもとにして、B組全員のハンドボール投げの記録について、箱ひげ図をかき入れなさい。

③ 図1、図2から読みとれることとして、次の(i)、(ii)は、「正しい」、「正しくない」、「図1、図2からはわからない」のどれか、下のア～ウから最も適切なものをそれぞれ1つ選び、その記号を書きなさい。
(i) ハンドボール投げの記録の第1四分位数は、A組とB組では同じである。
ア.正しい
イ.正しくない
ウ.図1、図2からはわからない

(ii) ハンドボール投げの記録が27m以上の人数は、A組のほうがB組より多い。
ア.正しい
イ.正しくない
ウ.図1、図2からはわからない

⑵ 下の〈問題〉について、次の各問いに答えなさい。

〈問題〉
Pさんは家から1200m離れた駅まで行くのに、はじめ分速50mで歩いていたが、
途中から駅まで分速90mで走ったところ、家から出発してちょうど20分後に駅に着いた。
Pさんが家から駅まで行くのに、歩いた道のりと、走った道のりを求めなさい。

下の▭は、まどかさんとかずとさんが、〈問題〉を解くために、それぞれの考え方で連立方程式に表したものである。

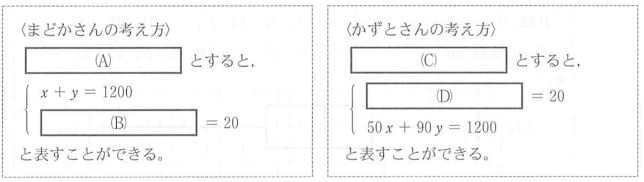
① 上の［　(A)　］～[　(D)　]に、それぞれあてはまることがらはどれか、次のア～コから最も適切なものを1つずつ選び、その記号を書きなさい。
ア. 歩いた道のりをx分、走った時間をym
イ. 歩いた時間をx分、走った時間をy分
ウ. x + y
エ. x – y
オ. 50x + 90y
カ. 90x + 50y　
キ. 50/x + 90/y
ク. 90/x + 50/y
ケ. x/50 + y/90
コ. x/90 + y/50

② Pさんが家から駅まで行くのに、歩いた道のりと走った道のりを、それぞれ求めなさい。

⑶ 次の図のように、1からnまでの自然数が順に1つずつ書かれたn枚のカードがある。このカードをよくきって1枚取り出すとき、取り出したカードに書かれた自然数を a とする。
このとき、次の各問いに答えなさい。

① n ₌ 10 のとき、√a が自然数となる確率を求めなさい。

② 12/a が自然数となる確率が1/2になるとき、n の値をすべて求めなさい。

解答・解説

(1) ①19
B組は18人(偶数)なので、中央値は9人目と10人目の平均値となる。
よって (18 + 20) ÷ 2 ₌ 19

②

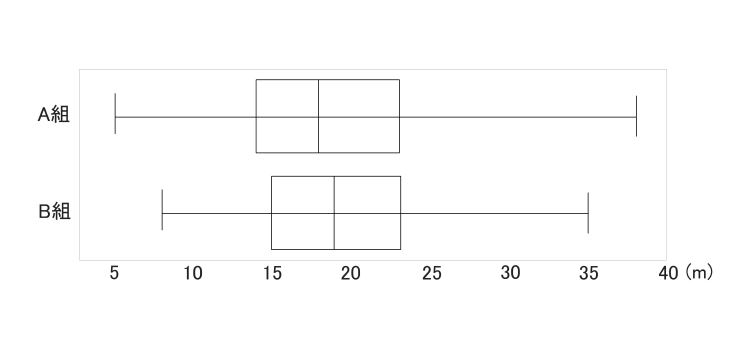
第1四分位数は全体の中央値未満の数を並べたその中央値となるため15
第3四分位数は全体の中央値より大きい数を並べたその中央値となるため23
最小値は 8 、最大値は 35 、中央値は 19
これを箱ひげ図へ記入する。

③ (i) イ
第1四分位数はA組 14 、B組 15となる。よって イ

(ii) ウ
箱ひげ図では27m以上投げた人の数はわからない。
A組で27m以上投げた人数が不明である　よって ウ

⑵ ① (A)ア　(B)ケ　(C)イ　(D)ウ
（まどかさんの考え方）
x + y ₌ 1200 とあるので、まどかさんは「道のり」を文字 x.y としている。
よって(A)は、「歩いた道のりをx、走った道のりをy」となる。
(B)については時間を求める式となっているため、x/50 + y/90 ₌ 20 となる。
（かずとさんの考え方）
50x + 90y ₌ 1200 とあるので、かずとさんは「時間」を文字 x.y としている。
よって(C)は「歩いた時間をx、走った時間をy」となる。
歩いた時間と走った時間の合計が20分なので、(D)は x + y ₌ 20 となる。
これらから、(A)はア、(B)はケ、(C)はイ、(D)はウとなる。
② 歩いた道のり 750m、走った道のり 450m
道のりを求めるので、まどかさんの考え方である連立方程式を解く。
x + y ₌ 1200 なので、x ₌ 1200 – y
x/50 + y/90 ₌ 20 の式の x に(1200 – y)を代入する。
(1200 – y)/50 + y/90 ₌ 20 両辺に450をかける。
10800 – 9y + 5y ₌ 9000　-4y ₌ -1800　 y ₌ 450
x + y ₌ 1200 の式のyに450を入れると、x + 450 ₌ 1200　x ₌ 1200 – 450　x ₌ 750
よって　歩いた道のり 750m、走った道のり 450m

(3) ① 3/10
1〜10までの数を入れて√aが自然数となるのは、√1、√4、√9の3通り。よって 3/10

② n ₌ 10 , 12
12/a が自然数になるのは、a が 12 の約数のときなので a ₌ 1 , 2 , 3 , 4 , 6 , 12 の 6通り
12/a が自然数になる確率が1/2なので、それを式で表すと(aの個数)/n ₌ 1/2 となる。
a の個数の最大は(1, 2, 3, 4, 6, 12)の6個なので、(aの個数)/n ₌ 1/2を満たす n は最大で 12 となる。

・a の個数が1個のとき、n ₌ 2 となる。
n ₌ 2 だとすると(aの個数)/nは 2/2 となるため成立しない。
・a の個数が2個のとき、n ₌ 4 となる。
n ₌ 4 だとすると(aの個数)/nは 4/4 となるため成立しない。
・a の個数が3個のとき、n ₌ 6 となる。
n ₌ 6 だとすると(aの個数)/nは 5/6 となるため成立しない。
・a の個数が4個のとき、n ₌ 8 となる。
n ₌ 8 だとすると(aの個数)/nは 5/8 となるため成立しない。
・a の個数が5個のとき、n ₌ 10 となる。
n ₌ 10 だとすると(aの個数)/nは 5/10 ₌ 1/2 となるため成立する。
・a の個数が6個のとき、n ₌ 12 となる。
n ₌ 12 だとすると(aの個数)/nは 6/12 ₌ 1/2 となるため成立する。

よって、12/a が自然数となる確率が1/2になるときのn の値は 10 , 12 となる。

大問3

問題文

次の図のように、関数 y ₌ 1/4x²・・・㋐のグラフ上に2点 A , B があり、点Aのx座標が-2、点Bのx座標が4である。3点 O , A , B を結び△OABをつくる。
このとき、あとの各問いに答えなさい。
ただし、原点をOとする。

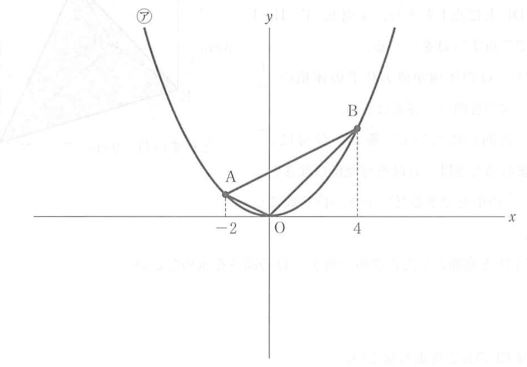
⑴ 点Aの座標を求めなさい。

⑵ 2点 A , B を通る直線の式を求めなさい。

⑶ x軸上の x ＞ 0 の範囲に2点 C , D をとり、△ABCと△ABDをつくる。
このとき、次の各問いに答えなさい。
なお、各問いにおいて、答えに√がふくまれるときは、√の中をできるだけ小さい自然数にしなさい。

① △OABの面積と△ABCの面積の比が 1：3 となるとき、点Cの座標を求めなさい。

② △ABDが∠ADB ₌ 90°の直角三角形となるとき、点Dの座標を求めなさい。

解答・解説

(1) (-2,1)
y ₌ 1/4x²のグラフ上の点Aはx座標が-2なので、y ₌ 1/4 × (-2)² ₌ 1 となる。よって(-2,1)

(2) y ₌ 1/2x + b
⑴と同じように点Bの座標を求めると、y ₌ 1/4 × 4² ₌ 4　点B(4,4)
次に直線ABの傾きを求める。
a ₌ yの増加量/xの増加量 ₌ (4 – 1)/(4 – (-2)) ₌ 3/6 ₌ 1/2
直線AB ₌ y ₌ 1/2x + b となり B(4,4)を入れてみると、4 ₌ 1/2 × 4 × b b ₌ 2 となる。
よって直線ABの式は y ₌ 1/2x + b となる。

(3) ① C(8 , 0)
直線ABで x が 0 のとき y ₌ 2
△OABと△ABCの面積比が 1：3 のとき、ABを底辺と考えると底辺が同じになるため
高さが3倍になると考えられる。
△OABは線分ABからOまでの距離が2なので、△ABCは線分ABからCまでの距離が6になる。
線分ABと平行な線上で、ABからCまでが6離れていて、 y ₌ 0 となる点Cを考える。
線分ABと平行なので傾きは 1/2 、ABから6離れるので切片bは 8 か -4
y ₌ 1/2x + 8 もしくは y ₌ 1/2x – 4
y ₌ 0 なので、0 ₌ 1/2x + 8 x ₌ -16　　　0 ₌ 1/2x – 4 x ₌ 8
x ＞ 0 とあるので、Cは y ₌ 1/2x – 4 にある点と分かる。　よって C(8 , 0)

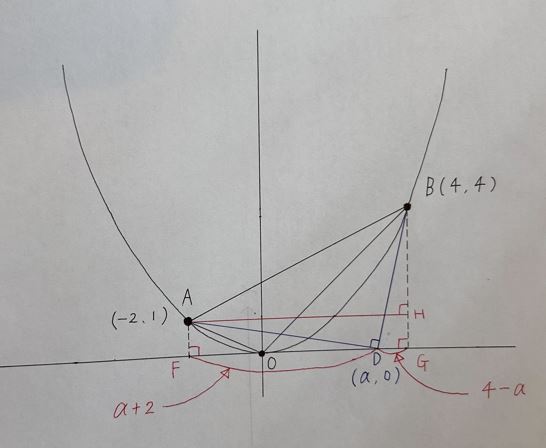
② D(1 + √5 , 0)
点Aと点Bからx軸に向けて垂線を引き、x軸との交点をそれぞれ点F、点Gとする。
三平方の定理を使用して考える
△AFDは直角三角形なので、AD² ₌ AF² ₌ FD² となる
Dはx軸上に有るため y ₌ 0 となりx座標をaとするとFDの長さは a + 2 となる
よって AD² ₌ 1² + (a + 2)² ₌ a² + 4a + 5
△BDGも直角三角形なので BD² ₌ BG² ₌ DG² となる
DGの長さは 4 – a　よって BD² ₌ 4² + (4 – a)² ₌ a² – 8a + 32
次に点Aからx軸上に平行な直線を引き、点Bから引いた垂線との交点を点Hとすると、
BHの長さは 3 　AHの長さは 6 となる
△ABHも直角三角形なので、AB² ₌ AH² + BH² となる
よって AB² ₌ 6² + 3² ₌ 45 となる
△ABDの∠ADBが直角となるという条件のため　AB² ₌ AD² + BD²
45 ₌ a² + 4a + 5 + a² – 8a + 32
2a² – 4a – 8 ₌ 0
解の公式より、(-(-4) ± √(-4)² – 4 × 2 × (-8))/2 × 2 ₌ (4 ± √80)/4 ₌ (4 ± 4√5)/4 ₌ 1 ± √5
a ₌ 1 ± √5 となるが x＞0という条件のため点Dの座標は 1 + √5 となる
よって点Dの座標は (1 + √5 , 0)

大問4

問題文

あとの各問いに答えなさい。

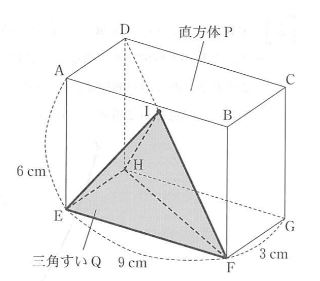
⑴ 図のように、点A、B、C、D、E、F、G、Hを頂点とし、AE ₌ 6cm、EF ₌ 9cm、
FG ₌ 3cmの直方体Pがある。直方体Pの対角線DF上に点Iをとり、4点E、F、H、Iを結んで三角すいQをつくる。
三角すいQの体積が直方体Pの体積の1/9のとき、次の各問いに答えなさい。
なお、各問いにおいて、答えの分母に√がふくまれるときは、分母を有理化しなさい。
また、√の中をできるだけ小さい自然数にしなさい。

① △EFHを底面としたときの三角すいQの高さを求めなさい。

② 線分EIの長さを求めなさい。

⑵ 次の図で、線分ABを直径とする半円の弧AB上に点Cがあり、線分ABの中点をOとするとき、∠OBD ₌ 90°、∠DOB ₌ ∠CAO となる直角三角形DOBを一つ、定規とコンパスを用いて作図しなさい。
なお、作図に用いた線は消さずに残しておきなさい。

解答・解説

(1) ① 4cm
全体の体積は 9 × 3 × 6 ₌ 162cm³
三角柱ABD-EFHは全体の半分なので81cm³
三角すいD-EFHの体積は三角柱ABD-EFHの1/3なので27cm³
問題より、三角すいQの体積は全体の1/9なので18cm³
なので三角すいD-EFHと三角すいQの体積比は 27：18 ₌ 3：2となる
底面が共通で体積比が3：2なので高さが3：2となる
三角すいD-EFHの高さは6cm　　よって三角すいQの高さは4cmとなる

(1) ② √29

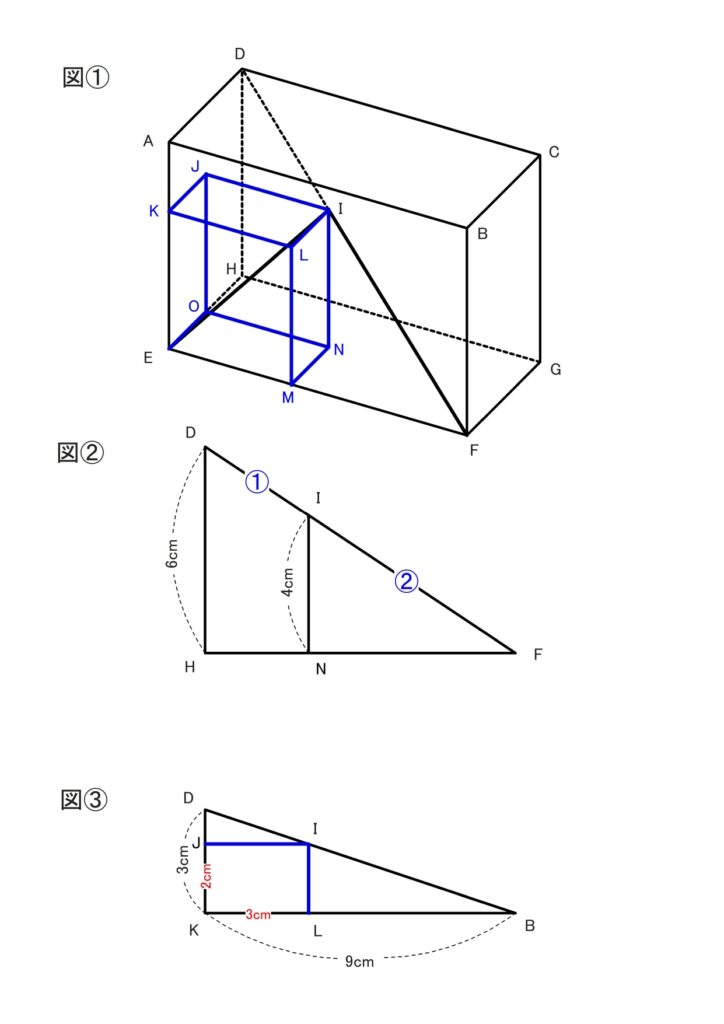
点Iから面EFGHに垂直な線を引く。［点N］
点Iから面AEHDに垂直な線を引く。［点J］
他も分かりやすくするため点Ｋ、Ｌ、Ｍ、Ｏを記したものが図①
△DHFと△INFの関係を表したものが図②となる
IN ₌ 4cmであることを先ほどの問い①で求めており、DH ₌ 6cmという前提なので
△DHFと△INFは相似比 3：2 の相似となる
これより DF：IFは 3：2 なので、DI：IFは 1：2 となる
次にこの立体を真上から見たのが図③で、真上から平面として捉えてみる
これも図②と同様に△DKBと△ILBは相似となり、DB：IBは 3：2 となる
3：2の相似のため、ILはDKの2/3の長さなので2cmとなる
同様に、LBもKBの長さの2/3となり6cmとなる　よってKLは3cm
KL ₌ EM ₌ 3cm　IL ₌ NM ₌ 2cm
三平方の定理より、EN² ₌ EM² + NM² ₌ 3² + 2² ₌ 13
再度、三平方の定理より、EI² ₌ EN² + IN² ₌ 13 + 4² ₌ 29　EI ₌ √29　よってEI ₌ √29cm

(2)

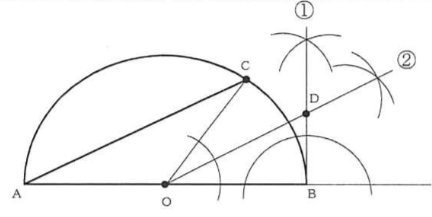
① ∠OBDが90°になるので、ABに対して垂直な線を引く。
ABをそのまま右に延ばす。
コンパスの中心を点Bに置き、点Oまでの長さをBOの反対側に記す。
この交点をXとする。
コンパスの中心を点Oと点Xに置き同じ半径で交わる点を求める。
点Bからその交点に直線を引く。

② 円周角の定理より∠CAOは∠COBの1/2の大きさになる。
∠COBの二等分線を引くとそれぞれの角は∠CAOと同じ大きさになる。
それを引くために点B、点Cからそれぞれ同じ半径の線を引き交点を出し、点Oからその交点に線を引く。
①で引いた線と②で引いた線の交点がDとなる。

大問5

問題文

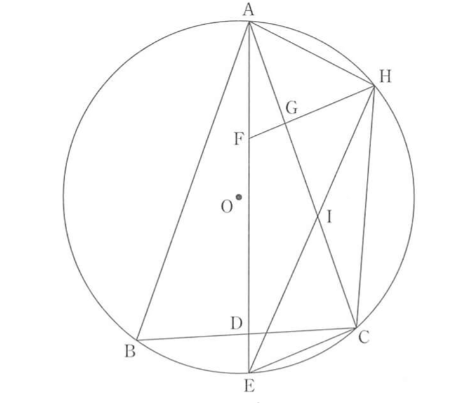
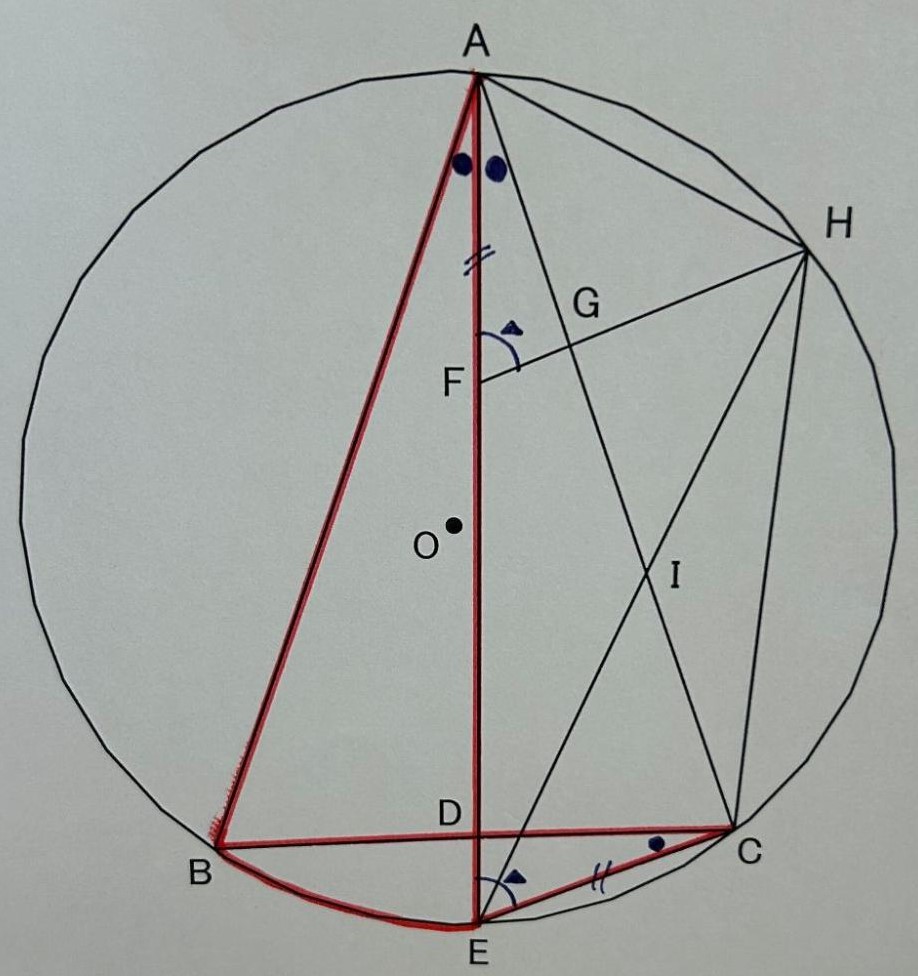
次の図のように、円Oの円周上に3点A、B、Cをとり、△ABCをつくる。∠BACの二等分線と線分BC、円Oとの交点をそれぞれD、Eとし、線分ECをひく。線分AE上に EC = AF となる点Fをとり、点Fを通り線分ECと平行な直線と線分AC、点Bをふくまない弧ACとの交点をそれぞれG、Hとし、線分AHと線分CHをひく。また、線分EHと線分ACとの交点をIとする。
このとき、あとの各問いに答えなさい。
ただし、点Eは点Aと異なる点とする。

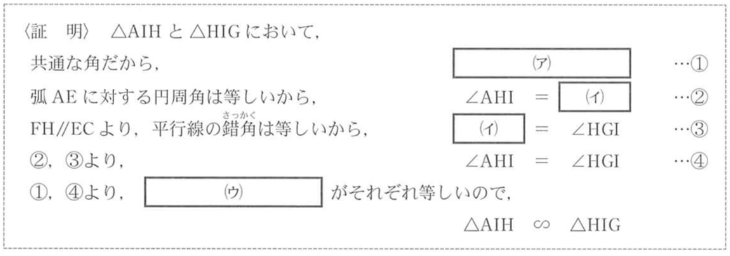
⑴ 次の▭は、△AIH∽△HIGであることを証明したものである。
[ （ア） ] ～ [ （ウ） ] に、それぞれあてはまる適切なことがらを書き入れなさい。

⑵ △AFG ≡ △CEDであることを証明しなさい。

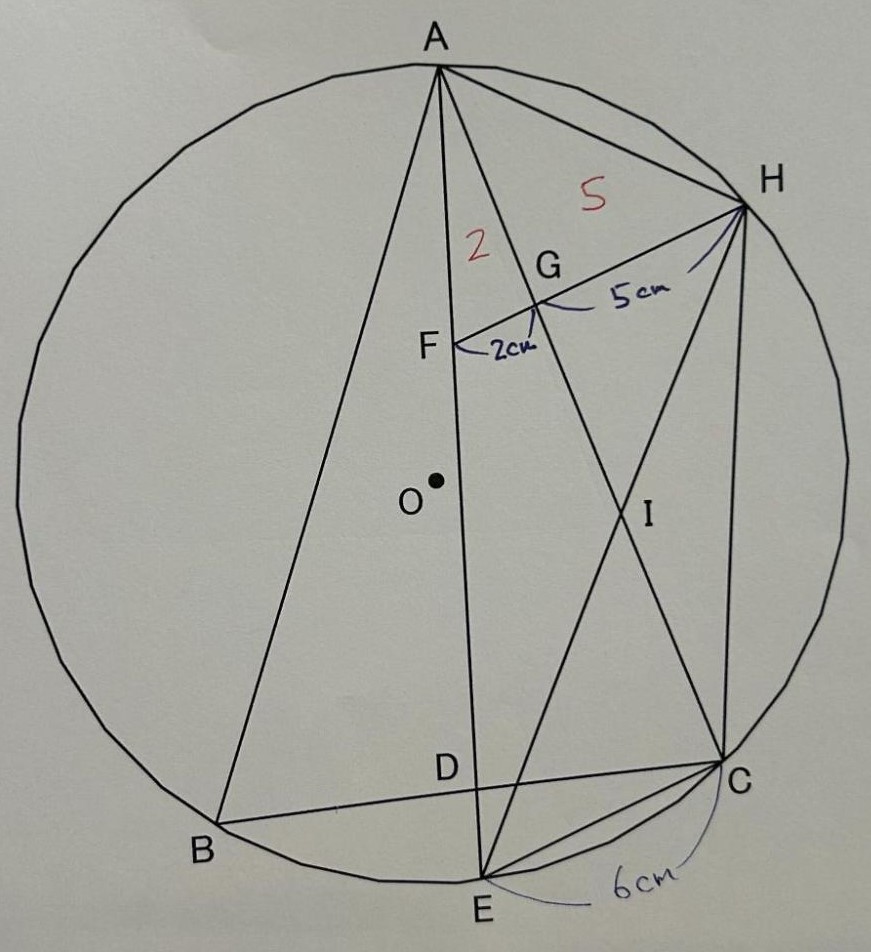
⑶ AF = 6cm、FG = 2cm、GH = 5cmのとき、次の各問いに答えなさい。
① 線分FEの長さを求めなさい。

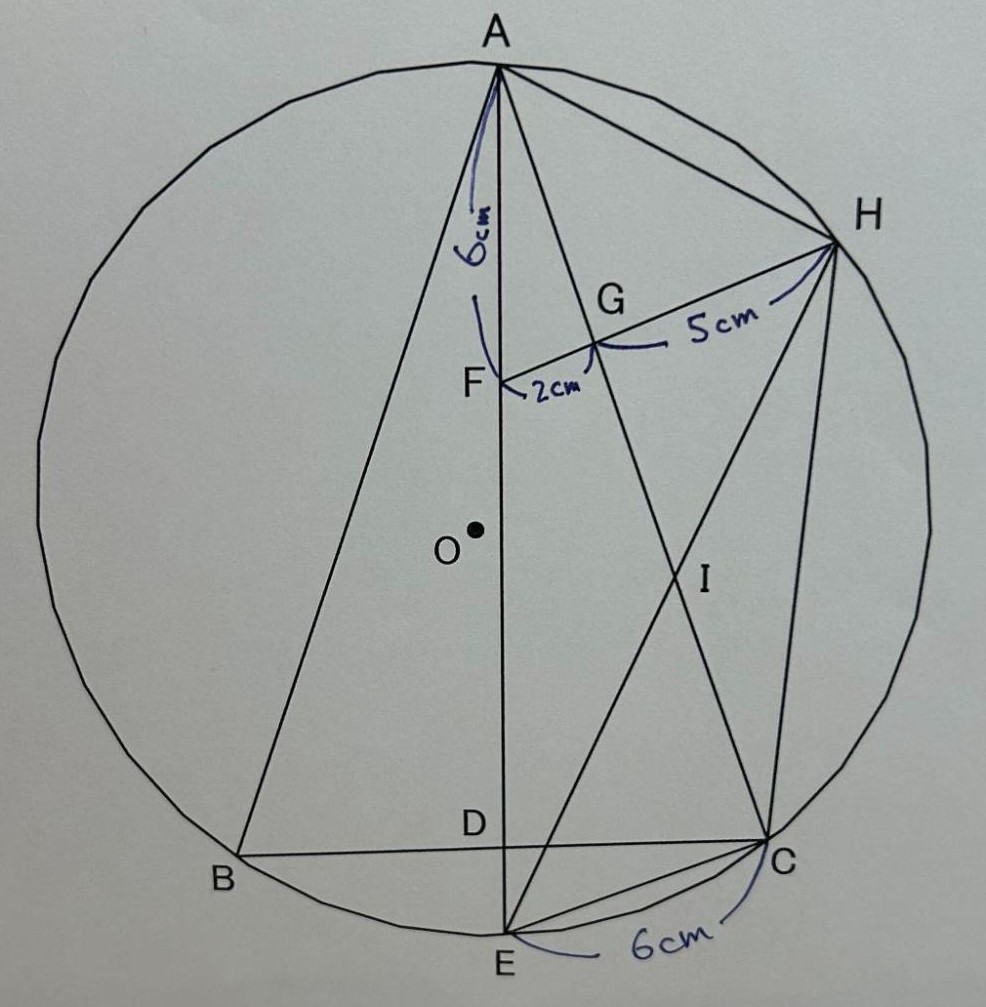
② △IECと△AGHの面積の比を、最も簡単な整数の比で表しなさい。

解答・解説

⑴ （ア）∠AIH = ∠HIG （イ）∠ACE （ウ）2組の角
（ア）共通の角は∠AIHと∠HIG    よって、あてはまるのは ∠AIH = ∠HIG
（イ）図にある弧AEの円周角は∠AHEと∠ACE。
 ∠AHEと∠AHIは同じなので∠AHIと∠ACEも同じといえる（円周角の定理で考える）…②
∠HGIと錯角の関係になるのは∠ACE…③
よって、あてはまるのは ∠ACE
（ウ）②は∠AHI = ∠ACE、③は∠ACE = ∠HGI
これを並べると∠AHI = ∠ACE = ∠HGI
①も④も角のことを述べているので、相似条件のうちの「2組の角がそれぞれ等しい」
に該当するため、あてはまるのは 2組の角

⑵ ＜証明＞
△AFGと△CEDにおいて、
仮定より、 AF = CE          ・・・①
線分AEは∠BACの二等分線だから、
        ∠BAE = ∠EAC           ・・・②
弧BEに対する円周角は等しいから、
        ∠BAE = ∠BCE           ・・・③
FH // ECより、平行線の同位角は等しいから、
        ∠AFH = ∠AEC           ・・・④
②、③より、
        ∠EAC = ∠BCE           ・・・⑤
①、④、⑤より、
1組の辺とその両端の角がそれぞれ等しいので、
       △AFG ≡ △CED

問題文より、AF = CE
線分AEは∠BACの二等分線なので、∠BAE = ∠EAC
弧BEで考えると円周角の定理より∠BAE = ∠BCE
上記の2点から、∠EAC = ∠BCEと分かる。
FHとECは平行で、平行な線にある同位角は等しいので∠AFH = ∠AECとなる
1組の辺とその両端の角が等しいと分かったため
△AFGと△CEDは合同であるといえる。

⑶ ① 12cm
FGとECは平行なので△AFGと△AECは相似
FG = 2cm EC = 6cmなので相似比は 2：6 = 1：3
これにより AE = 18cmと分かり、AEからAFの6cmを引けば FE = 12cmと分かる

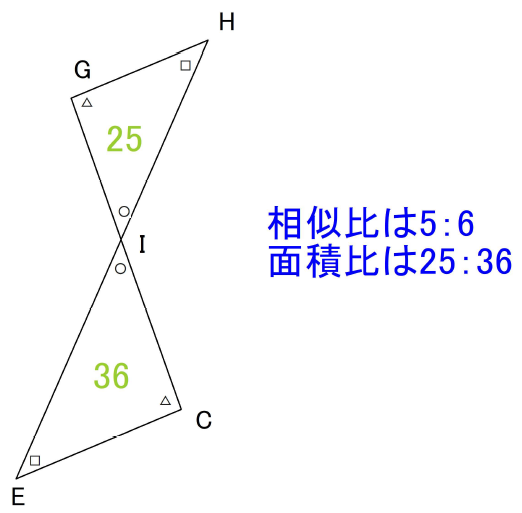
② 72：55

FG：GH = 2：5

△AFGと△AGHの高さは同じだと考えらえるので、
△AFGと△AGHの面積比は2：5となる
△AFGと△AECは相似比1：3の相似なので、AG：GCは1：2となる
GHの長さは5cm、ECの長さはAFと同じ6cmなので
相似の関係である△GHIと△IECの相似比は5：6
面積比は25：36となる

ACの関係を図にしてみると、

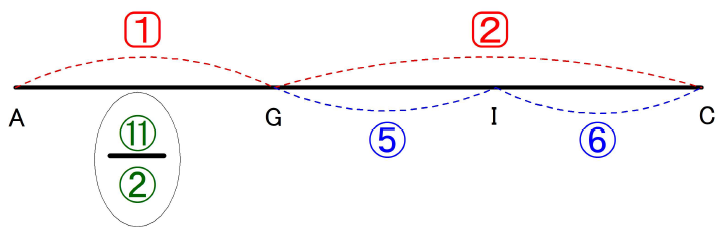
この図から分かるように、AG：GI = 11：10
△AGHと△GHIの高さは同じなので、△AGHと△GHIの面積比は11：10
△AGHの面積を5としたとき、△GHIは、10/11 × 5 = 50/11 となる
△GHIと△IECの面積比は25：36なので、
△GHIが50/11のとき△IEC = 36/25 × 50/11 = 72/11 となる
△IEC = 72/11 、△AGH = 5なので整数にして、72：55 よって 72：55

 三重県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！

教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！

受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。