奈良県の2020年3月実施の令和2年度（2020年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

奈良県の数学は4つの大問で構成され、そのうち1つが小問集合となっています。その他の大問は、関数・図形が出てくることが多く空間図形はあまりテーマになることはありません。
難易度は標準といったところです。数学が得意なお子さんであれば満点を狙えると思います。

 【奈良県】令和2年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら＞＞

 奈良県の公立高校入試情報はこちら

大問1：小問集合

（1）次の①～④を計算する問題です。
（1）①：5－8
【・答え「－3」】
5－8＝－3　

（1）②：－４×（－3）²
【・答え「9」】
※符号に注意
－4×(－3)²＝－36　
(－3)²＝(－3)×(－3)＝9　

（1）③：（4a³b+6ab²）÷2ab
【・答え「2a²+3b」】
(4a³b+6ab²)÷2ab=(4a³b+6ab²)/2ab
                               ＝2a²+3b

（1）④：（ｘ+ｙ）²－5ｘｙ
【・答え「ｘ²－3xy+ｙ²」】
(ｘ+ｙ)²－5xy＝ｘ²＋2xy+ｙ²-5xy
　　　　　　　＝ｘ²－3xy+ｙ²

（2）：絶対値が4より小さい整数は何個あるか答える問題です。
【・答え「7個」】
絶対値が４より小さい整数は、数直線上において、－4～4までの間の整数の数になるので、-3、-2、-1,0,1,2,3の７個になる。

（3）：2次方程式ｘ²+5ｘ+2＝0を解く問題です。
【・答え「(‐5±√17)/2」】
ｘ²+5ｘ+2＝0は、解の公式x=(‐b±√(ｂ^2-4ac))/2aを用いて、
ｘ＝(‐5±√(5²-4×) 1×2)/(2×1)
　=(‐5±√(25-8))/2
　＝(‐5±√17)/2

（4）：ｙがｘに反比例し、ｘとｙの値が表1のように対応しているとき、Aに当てはまる数を答える問題です。
【・答え「－６」】
反比例に関する問題です。
反比例なので、ｙ＝a/xとなる。
表１より、ｘ＝-3のとき、ｙ＝4なので、これを数式に当てはめると、
-4＝a/(-3)　よって、a＝12になり、ｙ＝12/x…①
表１のAは、ｘ＝-2のときのｙの値なので、それぞれ代入すると、
ｙ＝12/(-2)＝-6　よって、Aに当てはまる数字は-6となる。

（5）：図Ⅰは円錐の展開図で、底面の半径は5ｃｍ、側面のおうぎ形の半径は12ｃｍであるとき、∠ｘの大きさを求める問題です。
【・答え「∠ｘ＝150°」】
∠ｘに対する弧の長さは、半径５㎝の円の円周の長さなので、10π㎝。
次に、半径12㎝の円の円周の長さは、24π。中心角と弧の長さは比例するので、　
24π：10π＝360°：ｘ°
24ｘ＝3600
ｘ＝150　　
よって、∠ｘ＝150°

（6）：ある市における7月の日ごとの最高気温を度数分布表にまとめた表Ⅱから読み取れることとして適切なものをア～オの中からすべて選ぶ問題です。
【・答え「ア、エ」】
ア：5÷31＝0.161…より、適切。
イ：階級の幅はそれぞれ2℃なので不適切。
ウ：28℃以上の日は、5+7+5+5＝22日なので不適切。
エ：最頻値は(26.0+28.0)÷2＝27.0℃なので適切。
オ：階級値は（30.0+32.0）÷２＝31.0なので不適切。

（7）次の確率について述べた文章を見て①、②の問いに答える問題です。

（7）①：ｐの値を求める問題です。
【・答え「3/5」】
(i)偶数→奇数の順で取り出した場合
2/5×3/4＝6/20
(ii)奇数→偶数の順で取り出した場合
3/5×2/4＝6/20
(i)(ii)より、6/20+6/20＝3/5

（7）②：ｐの値とｑの値の関係について正しく述べているものをア～ウの中から選ぶ問題です。
【・答え「ウ」】
同様にｑの値を求めると、
(i)赤→白の順で取り出した場合
3/5×2/4＝6/20
(ii)白→赤の順に取り出した場合
　 2/5×3/4＝6/20
(i)(ii)より、6/20+6/20＝3/5　以上より、ｐとｑの値は等しい。

（8）一の位が0でない二桁の自然数Aがあり、Aの十の位と一の位の数を入れ替えて出来る数をBとするとき、①、②の問いに答える問題です。

（8）①：Aの十の位をｘ、一の位をｙとするとき、Bをｘ、ｙを用いて表す問題です。
【・答え「10y+x」】
Aが、10x+yなので、Aの十の位と一の位を入れ替えたBは、10y+xとなる。

（8）②：Aの十の位の数は一の位の数の2倍であり、BはAより36小さいとき、Aの値を求める問題です。
【・答え「A＝84」】
Aの10の位の数は一の位の数の2倍なので、A=10×2x+ｘとなる。Bは、Aの十の位と一の位を入れ替えた数なので、B=10x+2ｘ。さらに、Bは、Aの値より36小さいので、A＝B+36。
以上から、10×2ｘ+ｘ＝10x+2ｘ+36
9x＝36
x=4
よって、A＝10×2×4+4 ＝84

大問2：資料の活用

（1）：図4の四角形ABCDは、A判の規格の紙と相似な長方形です。辺BCは辺ABを1辺とする正方形ABEFの対角線の長さと等しいです。回答欄にある線分ABをもとに、点Cを作図する問題です。
【・答え「下図参照」】

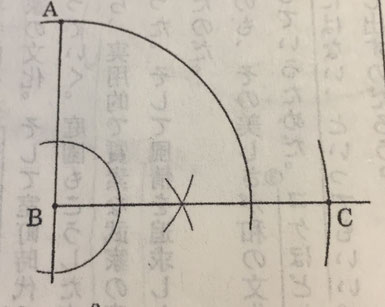
点Ｂを通る直線ＡＢの垂線上に点ＥをＢＥ＝ＡＢとなるようにとるとき点Ｃは直線ＢＥ上のＢＣ＝ＡＥとなる点である。
① 直線ＡＢの垂線を引く。
② 点Ｂを中心とした半径ＡＢの円を描き、垂線との交点をＥとする。
③ 点Ｂを中心として、半径ＡＥの円を描き、垂線との交点がＣとなる。

（2）A0判の紙の短い方の辺の長さをacmとするとき、①・②の問いに答える問題です。

（2）①：A1判の紙の短い方の辺の長さをaを用いて表す問題です。
【・答え「√2/2 a」】
A0判の辺の長さの比が、1：√2より、A0判の短い方の辺をa㎝とすると、長い方の辺の長さは、√2 aとなる。A1判は、A０判の半分なので、対応する辺も半分となる。よって、√2/2 aとなる。

（2）②：A3判の面積をaを用いて表す問題です。
【・答え「√2/8 a² （ｃｍ²）」】
A0の面積は、a× √2 a＝√2 a^2
A1の面積は、A0の半分なので、√2/2 a^2
A2の面積は、A１の半分なので、√2/2 a^2×1/2¬＝√2/4 a^2
A３の面積は、A２の面積の半分なので、√2/4 a^2×1/2＝√2/8 a^2

（3）A3判の資料を、コピー機でB6判に縮小して文集に使用することにしたときになされた会話をよみ、①・②の問いに答える問題です。

（3）①：「あ」に当てはまる数を小数第3位を四捨五入した値で答える問題です。
【・答え「1.22倍」】
A0とA3の関係より、対角線の長さは、√(1+2)＝√3
よって、1：√2＝ｘ：√3
ｘ＝√3/√2
＝√6/2
√6/2＝2.449/2
＝1.224….

（3）②：A3判の資料をB6判に縮小するには、何％の倍率にすればよいかを小数第1位を四捨五入した値で答える問題です。
【・答え「0.433倍」】
①より、A3とB3の関係は、√6/2倍。
B3→B4は、√6/2 ×√2/2 ※(2)①より、√2/2倍
B4→B5は、√6/2 ×√2/2×√2/2
B５→B6は、√6/2 ×√2/2×√2/2×√2/2＝(2√12)/16＝√3/4＝1.732/4＝0.433

大問3：二次関数

（1）：2点A,Cを通る直線の式を求める問題です。
【・答え「ｙ＝－2ｘ+4」】
ｙ＝－2ｘ+4　傾きが(2-8)/(1-（-2）)＝－2、A(1、2)を代入して、
2＝－2×1+ｂ
ｂ=4 よって、ｙ＝－2ｘ+4

（2）：関数ｙ＝2ｘ²についてア～エの中から変化の割合が最も大きくなるものを選び、その時の変化の割合を求める問題です。
【・答え「ア」】
それぞれの変化の割合を求めると、　
ア：6/1＝6　イ：8/2＝4　ウ：8/2＝4　エ：0/4＝0　以上より、変化の割合が最も大きくなるのはアである。

（3）：∠OPA＝45°となるとき、△OPAを、ｘ軸を軸として一回転させてできる立体の体積を求める問題です。
【・答え「4π（ｃｍ³）」】
点Aからｘ軸におろした垂線とｘ軸との交点をHとすると、△OPAは、ｘ軸を軸として回転させると、半径AHの円を底面にした、二つの円錐になる。
よって、
2×2×π×1×1/3+2×2×π×2×1/3＝4π

（4）：四角形APQCが平行四辺形となるとき、点Pのｘ座標を求める問題です。
【・答え「3+√3」】
点P（ｐ，0）、点Qのｙ座標をｑとする。AC//PQ、AC=PQより、点Aと点Cのｙ座標の差は、点Pと点Qのｙ座標の差に等しいので、
8－2＝q－0　ｑ＝６
点Qは、ｙ＝２ｘ^２上の点より、Ｑのｘ座標は、２ｘ^２＝6　ｘ＞0より、ｘ＝√3　よって、点Q(√3 、6)
同様にｘ座標の差も等しいので、１－(－２)＝ｐ－√3　よって、ｐ＝3+√3

大問4：平面図形

（1）：△AFE∽△BCEを証明する問題です。
【・答え「下記参照」】
(1) 仮定より、∠ＡＥＦ＝90°、∠ＢＥＣ＝90°、∠ＡＤＣ＝90°…①
また、△ＡＤＣにおいて、∠ＤＡＣ＝180°－90°－∠ＡＣＤ…②
△ＢＣＥにおいて、∠ＥＢＣ＝180°－90°－∠ＡＣＢ
よって、∠ＥＢＣ＝180°－90°－∠ＡＣＤ…③
②③より、∠ＤＡＣ＝∠ＥＢＣ
△ＡＦＥと△ＢＣＥにおいて、∠ＦＡＥ＝∠ＣＢＥ…④
①④より２組の角がそれぞれ等しいので△ＡＦＥ∽△ＢＣＥ

（2）：∠AFE＝a°のとき、∠OABの大きさをaを用いて表す問題です。
【・答え「90°－a°」】
△ＡＦＥ∽△ＢＣＥより、∠ＡＦＥ＝∠ＡＣＢ＝a°
弧ＡＢに対する円周角より∠ＡＣＢ＝∠ＡＧＢ＝a°
中心角と円周角の関係より∠ＡＯＢ＝２∠ＡＧＢ＝２a°
△ＯＡＢにおいて、ＯＡとＯＢは円の半径なので等しい。つまりＯＡ＝ＯＢの二等辺三角形である。
よって、∠ＯＡＢ＝(180°-∠ＡＯＢ)/2
＝(180°-2a°)/2
＝90°－a°

（3）BC=10cm、AF=2ｃｍ、DF＝3ｃｍのとき、①・②の問いに答える問題です。

（3）①：線分AGの長さを求める問題です。
【・答え「8」】
△ＦＢＧにおいて仮定より、∠ＦＤＢ＝∠ＧＤＢ＝90°…①
弧ＣＧにおいて円周角より、∠ＧＡＣ＝∠ＧＢＣ…②
△ＡＦＥ∽△ＢＣＥより、∠ＥＡＦ＝∠ＥＢＣ
つまり∠ＣＡＧ＝∠ＦＢＤ＝∠ＤＢＧ…③
△ＦＢＤと△ＤＢＧにおいて共通の辺なのでＢＤ＝ＢＤ…④
①～④より△ＦＤＢと△ＤＢＧは１つの辺とその両端の角がそれぞれ等しい　　　　　　　　　　
ので△ＦＤＢ≡△ＤＢＧ
よって、対応する円の長さは等しいのでＦＤ＝ＧＤ＝３
ＡＧ＝ＡＦ+ＦＤ+ＤＧ
＝2＋3＋3
＝8

（3）②：円Oの面積を求める問題です。
【・答え「36π（ｃｍ²）」】
弦ＢＣと弦ＡＧの垂直二等分線をそれぞれひくと点Ｏを通る。垂直二等分線
とそれぞれの弦との交点をＰ，Ｑとすると、ＢＰ＝ＢＣ/2＝5/2、
ＯＰ＝ＱＤ＝ＡＧ/2－ＤＧ＝8/2－3＝1
△ＯＢＰにおいて三平方の定理より、ＯＢ＝√(ＢＰ²+ＯＰ² )＝√(5² +1² )＝√26
よって円Ｏの半径は√26
以上より円Ｏの面積は、（√26）×（√26）×π＝36π（ｃｍ²）

 奈良県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、奈良県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。