【奈良県】令和5年度/2023年度入学者高校入試選抜試験：数学の解説

奈良県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。

受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。

また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 奈良県教育委員会のサイトこちら

次の各問いに答えよ。

(1) 次の①～④を計算せよ。

① 7-(-6)

②15+(-4)²÷(-2)

③(x+2)(x-5)-2(x-1) 

④√2×√6-√27

(2) 連立方程式 x+4y=5, 4x+7y=-16 を解け。

(3) 2次方程式x²+5x+1=0を解け。

(4) a<0,b<0のとき、a+b,a-b,ab,a/bのうちで、式の値が最も小さいものはどれか。 

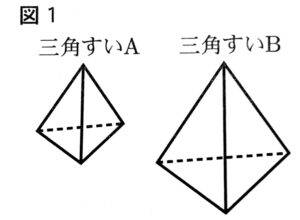
(5) 図1の2つの三角すいA、Bは相似であり、その相似比は2：3である。三角すいAの体積が24㎤であるとき、三角すいBの体積を求めよ。

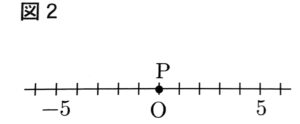
(6) 図2で数直線上を動く点Pは、最初原点Oにある。点Pは、1枚の硬貨を1回投げるごとに、表が出れば正の方向に1だけ移動し、裏が出れば負の方向に2だけ移動する。硬貨を3回投げて移動した結果、点Pが原点Oにある確立を求めよ。

(7) 省略。

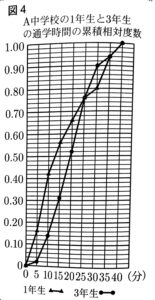
(8) A中学生の1年生75人と3年生90人に、通学時間についてアンケートをした。図4は、その結果について、累積相対度数を折れ線グラフに表したものである。例えば、このグラフから、1年生では通学時間が10分未満の生徒が、1年生全体の42%であることを読み取ることができる。図4から読み取ることができることがらとして適切なものを、次のア～オから全て選び、その記号を書け。

ア 数学時間の中央値は、1年生の方が3年生よりも大きい。

イ 通学時間が20分未満の生徒は、1年生も3年生も半分以上いる。

ウ 通学時間が25分未満の生徒の人数は、1年生も3年生も同じである。

エ 通学時間が25分以上30分未満の生徒の人数は、3年生の方が1年生よりも多い。

オ 全体の傾向としては、1年生の方が3年生よりも通学時間が短いといえる。

(1)

① 7-(-6)=7+6=13

②15+(-4)²÷(-2)=15+16÷(-2)=15+(-8)=15-8=7

③(x+2)(x-5)-2(x-1)=(x²-5x+2x-10)-2x+2=x²-3x-10-2x+2=x²-5x-8

④√2×√6-√27=√12-3√3=2√3-3√3=-√3

(2) x+4y=5・・・①、4x+7y=-16・・・②とする。

①の両辺に4をかけると、 4x+16y=20・・・③

③-②で、 9y=36 ∴y=4

y=4を①に代入して、 x+16=5 ∴x=-11

よって、 x=-11,y=4

(3) 2次方程式の解の公式を使って、

x=(-b±√(b²-4ac))/2a=(-5±√(25-4))/2=(-5±√21)/2

(4) 条件より、-b>0のため、 a+b<a-b

また、 a+b<0, ab>0, a/b>0 なので、a+bが最小値となる。

(5) 相似の図形の体積比は相似比の3乗に等しくなるため、体積比は2³：3³=8：27

よって三角すいBの体積は 24×(27/8)=81(㎤)

(6)最終的に点Pが原点Oにあるためには、表が2回、裏が1回出る必要がある(出る順番は関係ない)。

よって、

1/2×1/2×1/2×3=3/8

(7) 省略。

(8) イ、エ、オ

太郎さんと花子さんは、ロボット掃除機が部屋を走行する様子を見て、動く図形について興味をもった。次の---内は、いろいろな図形の内部を円や正方形が動くとき、円や正方形が通過する部分について考えている、太郎さんと花子さんの会話である。

-------------------------

花子：長方形の内部を円や正方形が動くとき、正方形は、長方形の内部をくまなく通過できるね。でも、円は、長方形の内部で通過できないところがあるよ。正方形は、どんな図形の内部でもくまなく通過できるのかな。

太郎：どうかな。三角形の内部では、円も正方形も通過できないところがあるよ。いろいろな図形の内部を円や正方形が動く場合、通過できるところに違いがあるね。

花子：直角二等辺三角形の内部を円や正方形が動くときについて、真上から見た図をかいて考えてみよう。

-------------------------

XZ=YZ,∠XZY=90°の直角二等辺三角形XYZの内部を円Ｏ、正方形ABCDが動くとき、各問いに答えよ。ただし、円周率はπとする。

(1) 図1で、円Oは辺XY,YZに接しており、2点P、Qはその接点である。また、点Ｒは直線XOと辺YZとの交点である。①～③の各問いに答えよ。

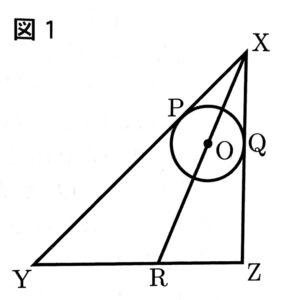
①∠POQの大きさを求めよ。

②線分XR上にある点はどのような点か。「辺」と「距離」の語を用いて簡潔に説明せよ。

③円Oの半径が2㎝であるとき、線分XPの長さを求めよ。

(2) 次の---内は、△XYZの内部を、正方形ABCDが動く場合について考えている、太郎と花子さんの会話である。①、②の問いに答えよ。

-------------------------

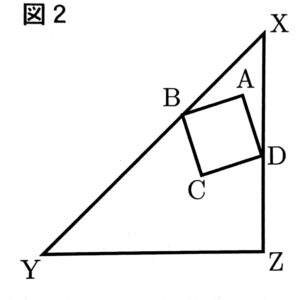
花子：図2のように、正方形ABCDが、点Xに最も近づくように、正方形ABCDの2点B,Dがそれぞれ辺XY,XZ上にある図をかいたよ。

太郎：図2の正方形ABCDで、点Xに最も近いのは点Aだね。

花子：そうだね。2点X,A間の距離はどのくらいの長さになっているのかな。図2からわかることは何だろう。

太郎：点Aを中心として2点B,Dを通る円をかくと、点Xも円Aの周上にありそうだね。

花子：円Aで、弧BDに対する中心角は∠BADになるね。∠BAD=90°で、∠BXD=45°だから、∠BXDは弧BDに対する円周角になっているね。点Xは円Aの周上にあるといえるよ。

太郎：2点X,A間の距離は【 あ 】と等しいといえるね。

花子：正方形ABCDが動いて、辺XY,XZ上の2点B,Dの位置が変わっても、2点X,A間の距離について同じことがいえるから、正方形ABCDが、△XYZの内部をくまなく動くとき、正方形ABCDが通過した部分の面積もわかるね。

-------------------------

①【 あ 】にあてはまる語句を、次のア～エから1つ選び、その記号を書け。

ア 正方形ABCDの対角線の長さ

イ 正方形ABCDの1辺の長さ

ウ 正方形ABCDの対角線の長さの半分

エ 正方形ABCDの1辺の長さの半分

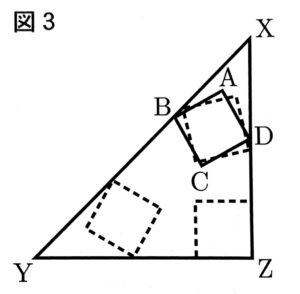
②図3のように、正方形ABCDが、△XYZの内部をくまなく動くとき、正方形ABCDが通過した部分の面積を求めよ。ただし、XZ=10㎝、AB=3㎝とする。

(1) 

①∠XPO=90°、∠XQO=90°、∠YXZ=45°なので、

∠POQ=360°-90°-90°-45°=135°・・・(A)

②2辺XY、XZからの距離が等しい点。

③直線OQとと線分XYの交点をSとする。

線分XOは∠SXQの二等分線なので、XS：XO=SO：QO

ここで、△XSQは直角二等辺三角形より、

XS：XQ=√2：1となるので、

SO：QO=√2：1

SO：2=√2：1 ∴SO=2√2(㎝)

よって、XP=XQ=SQ=2+2√2(㎝)・・・(A)

(2) 

①イ

②(10×10×1/2) - (3²×π×45/360×2)

=50-9π/4(㎠)・・・(A)

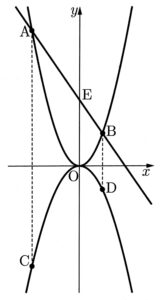
 右の図のように、関数y=ax²（a>0）のグラフ上に、2点A、Bがあり、関数y=(-½)x²のグラフ上に2点C、Dがある。

2点A、Ｃのx座標は-4であり、2点B、Dのx座標は2である。

2点A、Ｂを通る直線とy軸との交点をＥとする。原点をＯとして、各問いに答えよ。

(1) 関数y=(-½)x²について、xの変域が-4≦x≦2のときのyの変域を求めよ。

(2) 2点C、Dを通る直線の式を求めよ。

(3) aの値が大きくなるとき、それにともなって小さくなるものを、次のア～エから1つ選び、その記号を書け。

ア 直線ABの傾き

イ 線分ABの長さ

ウ △OABの面積

エ AE：EBの比の値

(4) 直線ODが四角形ACDBの面積を2等分するとき、aの値を求めよ。

(1)yはxが-4のとき最小値、xが0のとき最大値をとるので、それぞれ代入して

-8≦y≦0・・・(A)

(2)2点C、Dそれぞれの座標は、C(-4,-8) D(2,-2)となる。

よって求める式の傾きは 6/6=1

傾き1の直線がD(2,-2)を通るので、 y=x-4・・・(A)

(3)(-4,16a)、B(2,4a)となる。

ア (4a-16a)/(2-(-4))=-2a

イ √((2-(-4))²-(4a-16a)²)=√(36+144a²)

ウ 直線ABの式を、y=-2ax+bとすると、B(2,4a)を通るので、4a=-4a+b ∴b=8a

よって、E(0,8a)となるので、

△OAB=1/2×8a×(2-(-4))=24a

エ AE：EB=4：2=2：1

よって、答えはア

(4)直線ODと直線ACの交点をFとする。直線ODの式は、y=-xより、点Fの座標は(-4,4)となる。

四角形ACDBは台形なので、直線ODが面積を2等分するのは、AF+BD=FCとなるとき。

よって、

(16a-4)+(4a-(-2))=4-(-8)

20a=14 ∴a=7/10・・・(A)

図で、4点A,B,C,Dは円Oの周上にある。点Eは線分ACと線分BDとの交点でAC⊥BDであり、点Fは線分AD上の点で、EF⊥ADである。点Gは直線EFと線分BCとの交点である。各問いに答えよ。

(1) △AEF∽△BCEを照明せよ。

(2) ∠DAE=a°とするとき、∠BGEの大きさをaを用いて表せ。

(3) DE=3㎝、AE=4㎝、BE=8㎝のとき、①、②の問いに答えよ。

① △CEGの面積を求めよ。

② 円Oの半径を求めよ。

(1) △AEFと△BCEにおいて、仮定より、

∠AFE=90°・・・①

∠BEC=90°・・・②

①、②より、∠AFE=∠BEC・・・③

1つの弧に対する円周角は等しいので、 ∠EAF=∠CBE・・・④

③、④より、2組の角がそれぞれ等しいので、△AEF∽△BCE

(2) ∠CBE=∠DAE=a°より、

∠BCE=180°-90°-a°=90°-a°より、

∠GEC=∠AEF=90°-a°

よって、∠BGE=∠GCE+∠GEC=(90°-a°)+(90°-a°)=180°-2a°・・・(A)

(3) 

 ① ∠BEG=180°-(180°-2a°)-a°=a°より、

∠GBE=∠GEB=a°となるので、GB=GE

また、∠GEC=∠GCE=90°-a°より、GC=GEとなるので、GB=GCとなる。

ここで、△BEC∽△AEDより、

CE：DE=BE：AE

CE：3=8：4

4CE=24

CE=6(㎝)

よって、△CEG=1/2×6×8×1/2=12(㎠)・・・(A)

② 図のように点Hをとると、△ABEにおいて、三平方の定理より、

AB²=8²+4²=80

AB>0より、 AB=4√5(㎝)

ここで、∠BHA=∠BDAより、△ABH∽△AEDとなるので、

BH：ED=AB：AE

BH：3=4√5：4

4BH=12√5 ∴BH=3√5(㎝)

△ABHにおいて、三平方の定理より、

AH²=(4√5)²+(3√5)²=125

AH>0より、AH=5√5(㎝)

よって、円Ｏの半径は、5√5/2(㎝)・・・(Ａ)

 奈良県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストでは、お子さんに合った受験対策ができるよう、受験生を中心に、体験授業の際や担当家庭教師との事前研修の際にも志望校や入試を見据えて指導方針を考えています！

ご家庭と、担当家庭教師、アシストの連携がしっかりしているからこそ、安心して受験に臨むことができる授業にすることができるんです！指導を進めながら、志望校のご相談に乗ったり、成績に合わせて志望校を決めたり…学校の面談だけでは決めきれない場合や悩んでしまう場合もぜひお任せください！

普段の予習復習など、学校の内容に合わせた授業はもちろん、それらに関連付けながら過去問の解説などの受験対策も行っていくことができるので、効率よく普段の勉強と受験勉強の両立ができます！ 

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

私たち家庭教師のやる気アシストでは、体験授業の際に高校受験を見据えた勉強のやり方やコツを教えています。勉強には必ずつながりがあるので、入試目前に詰め込み学習をするよりも、なるべく早く受験に向けての姿勢づくりをしていった方がお子さん自身の負担が少なくなり、理解度も上がるので、高校に進学してからも勉強でつまずきにくくなります！

体験を受けることによって、受験に向けての道筋がはっきりするから勉強のやる気がでて、なおかつそのやる気を持続させることができるんです！

「勉強のやり方がわからない…」「何から手を付けたらいいかわからない …」というお子さんはぜひ私たちの体験授業を受けてやる気アップのきっかけにしてください！

『家庭教師ってどんな感じ？』『体験だけでもいいの？』『今の勉強方法と比べてみたい』そんな気持ちを持っている保護者さまほど、お役に立てる自信がありますのでお気軽にご相談ください。
私たちやる気アシストは、勉強で悩んでいるお子さんや保護者さまにとって、『無料の体験授業』がこれから大切な一歩を踏み出すキッカケ になれば嬉しいです。

 よく読まれている記事