大阪府の2019年3月実施の平成31年度（2019年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

大阪府の数学問題は、レベル別にＡＢＣの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Ａが易、Ｂがやや難、Ｃが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。

 【大阪府】平成31年度一般入学者選抜の過去問はこちらから
数学Ａの過去問題はこちら＞＞
数学Ｂの過去問題はこちら＞＞
数学Ｃの過去問題はこちら＞＞

 大阪府の公立高校入試情報はこちら

【数学Ａ】大問1：小問集合

問1：正負の数

問1：２ー(ー５)を計算する問題です。
【・答え「7」】
 与式=2+5=7
マイナス符号のついた（）内の数字は符号が入れ替わるので注意。

問2：正負の数

問2：－９×４/３を計算する問題です。
【・答え「-12」】
 与式=-3×4=-12
マイナスの付け忘れ注意。

問3：乗法と除法

問3：１３ー４²を計算する問題です。
【・答え「-3」】
与式=13-16=-3
（）のつかない累乗は符号の変化はないので注意。

問4：文字と式

問4：3ｘ＋７＋３（ｘ－２）を計算する問題です。
【・答え「6x+1」】
与式=3x+7+3x-6=6x+1　
掛け算から計算していく。順番に気を付けよう。文字のついた数字は同じ文字同士でしか計算できない。

問5：文字式の計算

問5：４ｘ²×２ｘを計算する問題です。
【・答え「8ｘ³」】
与式=4ｘ2ｘ²×ｘ=8ｘ³　累乗は全体に同じ文字がいくつあるか確認しよう。

問6：平方根の計算

問6：√５０－３√２を計算する問題です。
【・答え「2√2」】
与式=5√2-3√2=2√2　　平方根内の数字が同じか確認してから計算しよう。

大問2：小問集合

問1：文字式の計算

問1：ａ＝２のときの６ａー４の値を計算する問題です。
【・答え「８」】
与式=6×2-4＝8　代入法をしっかり見直そう。

問2：不等式

問2：数量の関係を正しく表した選択肢を選ぶ問題です。
【・答え「イ」】
配った色紙の枚数の合計は９x枚である。問題上50枚より多いとの事で>の記号を使用する。９X > 50のイとなる。文章題は読み間違えないように線を重要な部分には線を引きな　 がら問題に取り組もう。

問3：比例の関係

問3：ｘ：６＝５：３を満たすｘの値を計算する問題です。
【・答え「x=10」】
3x=5×6　3x=30　x=10　比例の計算は内項の積＝外項の積を覚えておこう。

問4：資料の活用

問4：表から10人の垂直とびの記録の最頻値を求める問題です。
【・答え「55」】
最も人数が多い記録を探す。55cmが４人と最も多い。よって最頻値は55cmである。

問5：連立方程式

問5：３ｘ＋ｙ＝１１とｘ－ｙ＝５の連立方程式を解き、ｘとｙの解を求める問題です。
【・答え「x=4　y=-1」】
3x+y=11‥①　x-y=5‥②　とする。①∔②でｙを式から消す。
3x+x=11+5　4x=16　x=4
①の式にx=4を代入すると　3×4+y=11　12+y=11　y=-1
連立方程式はいかに片方の文字だけの式にするかが大切。

問6：コインの確率

問6：二つの硬貨を同時に投げた時、同時に裏が出る確率を計算する問題です。
【・答え「1/4」】
２枚の硬貨の表裏の出方を樹形図を使って調べよう。
樹形図の通り４通りの出方をする。そのうち２枚とも裏が出るのは１通りなので　1/4になります。

問7：二次方程式

問7：ｘ²＋９ｘ＋１４＝０を解き、ｘの解を求める問題です。
【・答え「x=-7,x=-2」】
２次方程式はたすき掛けを使って解いてみよう。

問8：比例とグラフ

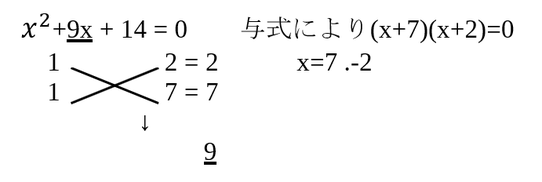
問8：ａとｂが正の定数のときのｙ＝ａｘ＋ｂを表したグラフを選択肢から選ぶ問題です。
【・答え「ア」】
関数y=ax+bのグラフは直線である。傾きつまりaの値が正であるため右上がりになる。
負ならば右下がりになる。切片つまりbの値はｙ座標との交点になる。a,b共に正であるためにアが正解となる。

問9：放物線

問9：ｙ＝ａｘ²（ａは定数）で（－３，５）を通るときのａの値を求める問題です。
【・答え「5/9」】
ｙ＝ａｘ²にAの座標を代入する。
5=a×(-3)²より、　a=5/9

問10：投影図

問10 ①：円錐の投影図である選択肢を選ぶ問題です。
【・答え「エ」】
立面図とは真正面から図形を見た図であり、この問題の場合三角形でなければならない。
平面図は真上から図形を見た図であり、この問題の場合円に見えなければならない。よって、エが正解となる。
問10 ②：底面の半径が４cm、高さが６cmの円錐の体積を求める問題です。

【・答え「32π㎤」】
円錐の体積の公式は1/3× (底面積) × (高さ) である。
底面積は42π=16π(㎠)なので、体積は1/3× 16π × 6 = 32π(㎠)　となる

大問3：一次関数

前脚と後脚までの幅が４０cmである椅子が前後に並べられています。「椅子の個数」をｘ個、「線分OPの長さ」をｙcmとしたときに、以下の問題を解いていく大問です。
関係を読み取って関係式を求めることができれば、問3まで簡単に解くことができます。

問1

問1：ｘとｙの関係を示した表中の(ア)(イ)に当てはまる数を求める問題です。
【・答え「ア：310　イ：５８０」】 表を見ると、xが1増えるとyは90増える。そのためxが2から4になると2増えているため2×90=180増える。130+180=310　310（ア）となる。またxが4から7まで3増えているyは90×3=270増える。310+270=580　580（イ）となる。

問2

問2：「椅子の個数」と「線分OPの長さの関係」を、ｙをｘの式で表す問題です。
【・答え「90x-50」】
x=1の時y=40であり、xが1増えると90増えるのだから、y=40+90(x-1)=90x-50となる。
yをxの式で表しなさいという問題はよく出ます。y=(xが含まれた式)の形を崩さずに文章をよく読みながら作ってあげて下さい。

問3

問3：ｙ＝1660となるときのｘの値を求める問題です。
【・答え　「19」】
y=90x-50にy=1660を代入すると、1600=90x-50　x=19　よって19となる。

大問4：平面図形

正方形ABCDと正方形DEFG(>正方形ABCD)があり、線分BCの延長線上に点Eがくるように置かれています。線分DCに対して平行となるように引かれた点Eからの直線と線分DGの交点を点Hとしたとき、以下の問題に解いていく大問です。

平方根や三角形の面積、平行関係の線分の関係など、基本的な内容が分かっていれば解くことが出来ます。

問1

問1：正方形ABCDの対角線ACの長さを求める問題です。
【・答え「3√2」】
ACの長さを求めるうえで必要なのが三平方の定理になります。△ABCを見ると二等辺三角形になっていることが分かります。
AB：BCが1：√2なので
AC＝√2AB＝3√2(cm)

問2

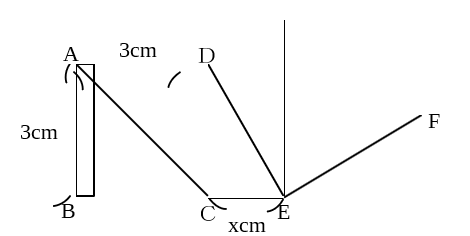
問2：△DCEの面積をｘを用いて表す問題です。
【・答え　「3/2x」】
DC＝3cm　CE=xcm　∠DCE=90°　なので△DCEは　1/2× CE × DC = 1/2× x × 3 =3/2x(㎠) となる。

問3

問3：△DCE∽△EDHであることの証明として示されている文の空欄a,bに適している文字をそれぞれ書く問題です。
【・答え「Ⓐ EDH　Ⓑ DEH　Ⓒウ」　】
証明問題は難しそうに見えてとても簡単！相似条件、合同条件をしっかり覚えて文章にあてはめていこう。

問4

問4：ｘ＝２であるときの線分DHの長さを求める問題です。
【・答え　「(2√13)/3」】
△DCE∽△EDHでCE=x=2㎝だから、相似比が分かればDHを求めることができる。
∠DCE=90°だから、三平方の定理により、DE=√(CE²+DC² )=√(2²+3² )=√13(㎠)
よって、△DCEと△EDHの相似比は、CE:DE=3:√13なので、DH=√13/3CE
=√13/3×2=2√13/3(㎠)

【数学B】大問1：小問集合

問1：乗法と除法

問1：４²ー（－６）÷２を計算する問題です。
【・答え「19」】
 与式=16-(-3)=16+3=19
マイナス符号のついた（）内の数字は符号が入れ替わるので注意しよう。

問2：文字式の計算

問2：２（５ａー３ｂ）ー７（ａー２ｂ）を計算する問題です。
【・答え「3a+8b」】
与式=10a-6b-7a+14b=3a+8b
文字のついた数字は同じ文字同士でしか計算できない。

問3：文字式の計算

問3：１８ｘｙ³÷（－３ｙ）²を計算する問題です。
【・答え「2xy」】
与式=18xy2÷9y2=2xy
()の外についた累乗は中の符号を変化させるので注意。

問4：平方根の計算

問4：（√７＋２√５）（√７－２√５）を計算する問題です。
【・答え「-13」】
与式=7-20=-13
(√7+2√5)(√7-2√5) →(A+B)(A-B)=A²-B²
この形は良く出るので覚えておこう！

問5：資料の活用

問5：度数分布表から最頻値を求める問題です。
【・答え「115」】
まずは最も大きい階級のものを探す。今回の場合は110g～120gになります。
最頻値はこの階級の階級値になるので(110+120)/2=115g　となる。

問6：正負の数

問6：ａ,ｂを負の数とするとき、ａ,ｂの絶対値によらず常に負となるものを選択肢から選ぶ問題です。
【・答え「イ」】
ア：負の数×負の数は正の数となる。イ：負の数+負の数は負の数となる 。ウ：イの逆になるので正の数 エ：数を2乗した場合必ず0以上の数になる。
よって　イ　が正解となります

問7：二次方程式

問7：（ｘ＋４）cmの辺と（ｘ＋５）cmの辺で構成された長方形の面積が２１０cm²のときのｘの値を求める問題です。
【・答え「10」】
縦が(x+4)㎝　横が(x+5)㎝　面積が210㎠　の長方形が出来たとの事。
(x+4)(x+5)=210　x2+9x+20=210　 x2+9x-190=0　
(x+19)(x-10)=0　x=-19.10　x＞0より　x=10
文章題はしっかり文字式におこすことから始めてみよう。

問8：確率

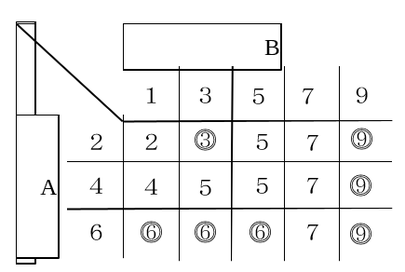
問8：２，４，６のカードが入った箱Aと１，３，５，７，９のカードが入った箱Bから同時に１枚取り出したときの大きい方の数が３の倍数である確率を求める問題です。
【・答え「7/15」】
全ての取り出し方とaの値を下の表のようにまとめた。全部で15通りとなり、その中で3の倍数になるものは〇印のものになる。
7通り確率の問題は樹形図や表を使って視覚的に分かりやすくしてから解くのがコツ！丁寧に解こう。

問9：放物線

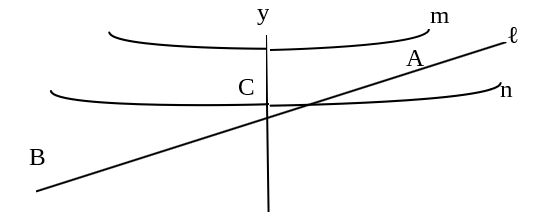
問9：２つの放物線を横切る一次関数ℓのｙ切片を求める問題です。
【・答え「33/10」】
Aは放物線y=x2上の点だから、x=2を代入するとA(2,4)である。
Bは放物線y=1/4 x^2上の点だから、x= -3を代入するとB(-3,9/4)である。
2点A,Bを通る直線ℓの傾きは(4-9/4)/(2-(-3))=7/20より7/20となる。
y=7/20 x+aに(2,4)を代入してa=33/10となる。よってCのy座標は33/10となる。

大問2：一次関数

前脚と後脚までの幅が４０cmである椅子が前後に並べられています。「椅子の個数」をｘ個、「線分OPの長さ」をｙcmとしたときに、以下の問題を解いていく大問です。

関係を読み取って関係式を求めることができれば、問1までは簡単に解くことができます。

問1 ①

問1 ①：ｘとｙの関係を示した表中の(ア)(イ)に当てはまる数を求める問題です。
【・答え「ア：310　イ：580」】
表を見ると、xが1増えるとyは90増える。そのためxが2から4になると2増えているため2×90=180増える。130+180=310　310（ア）となる。またxが4から7まで3増えているyは90×3=270増える。310+270=580　580（イ）となる。

問1 ②

問1 ②：「椅子の個数」と「線分OPの長さの関係」を、ｙをｘの式で表す問題です。
【・答え「90x-50」】
x=1の時、y=40であり、xが1増えると90増えるのだから、y=40+90(x-1)=90x-50となる。
yをxの式で表しなさいという問題はよく出ます。
y=(xが含まれた式)の形を崩さずに文章をよく読みながら作ってあげて下さい。

問1 ③

問1 ③：ｙ＝1660となるときのｘの値を求める問題です。
【・答え「19」】
y=90x-50にy=1660を代入すると、1600=90x-50　x=19
よって19となる。

問2

問2：PQが２００cm、OP間の椅子の個数が２３、QR間の椅子の個数が１６と分かっているときにORが３４９０cmとなる場合の、「前脚から後脚までの幅」ａを求める問題です。
【・答え「82」】
OP間の椅子の個数は23個なのでOP間の距離は90×23-50=2020　2020 cmとなる。
QR間の椅子の個数は16個なのでQR間の距離は40+(16-1)a=40+15a　40+15a cmとなる。
またQR間の距離は200 cmであり、OR間の距離は3490 cmであり、 OP間、PQ間、QR間の距離の和にあたるので、2020+40+15a+200=3490 である。
これをaについてとくとa=43　よってaの値は82となる。

大問3：平面図形

三角形ABCと長方形ECGFがあり、点Eは線分ABの間、点Fは線分ACの間に置かれています。点Aから線分BCに対して垂直にひいた線と線分BCが交差する点を点D、線分BCと線分EGとの交点をHとしたとき、次の問題を解いていく大問です。

問1

問1：∠AEFをａ°としたときの∠EAFの大きさをａ°を用いて表す問題です。
【・答え「90-a」】
⊿AEFについて、∠AEF=a°、∠AFE=90°である。⊿AEFの内角の和は180°なので、∠EAF=180-∠ AFE-∠AEF=90-a

問2

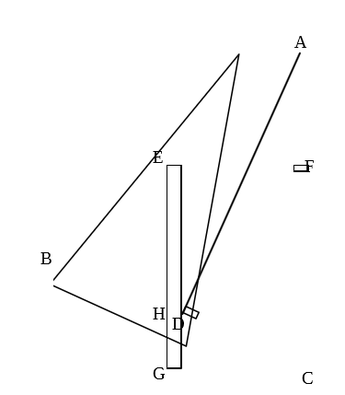
問2：△ABDと△CHGが相似であることを証明する問題です。
【・答え　
仮定より∠HGC=∠BDA=90° …①
EGとFCが平行であるので、∠GHC=∠ACB
仮定より⊿ABCは二等辺三角形であるので∠ACB=∠ABC
∠ABC=∠DBAであるので∠GHC=∠DAB …②
①②より二つの角がそれぞれ等しいので△ABD∽△CHG　】

証明問題は難しそうに見えてとても簡。相似条件、合同条件をしっかり覚えて文章にあてはめていこう。

問3 ①

問3 ①：HG＝２cm，HC＝５cmであるときの、線分BDの長さを求める問題です。
【・答え「22/5」】
△ABD∽△CHGより、AB:CH=HG:BDである。仮定よりAB=11、CH=5、HG=2より11:5=BD:2なので、これをといてBD=22/5

問3 ②：HG＝２cm，HC＝５cmであるときの、線分FCの長さを求める問題です。
【・答え「27/4」】
Dは二等辺三角形ABCの底辺の中点でありBD=22/5よりBC=44/5
HC=5であるのでBH=BC-HC=44/5-5=19/5
△BEH∽△BACより、BH:BC=EH:ACである。BH=19/5、BC=44/5、AC=11より19/5:44/5=EH:11なので、これをといてEH=19/4
よってFC=EG＝EH+HG=19/4+2=27/4

大問4：立体図形

四角柱ABCD-EFGHをもとに、以下の問題に解いていく大問です。

問1 ①

問1 ①：四角形EICFがひし形であるとき、AEとねじれの位置にある辺を選択肢から選ぶ問題です。
【・答え「エ」】
辺DH、辺CG、辺BFは辺AEと平行。
平行でなく、交わってもない位置関係をねじれの位置という。

問1 ②

問1 ②：四角形EICFがひし形であるときの四角形EFGHの対角線EGを求める問題です。
【・答え「4√2」】
四角形ABCDと四角形EFGHは合同
なので、EH=HG=4、よって△EHGは直角二等辺三角形。
そのため、三平方の定理よりEG=4√2

問1 ③

問1 ③：四角形EICFがひし形であるときの四角形EFGHの面積を求める問題です。
【・答え「8√6」】
辺CI、辺FE、辺FE、辺EIはいずれも底辺４、高さ２の直角三角形の斜辺である。(辺EHの中点Jとして辺IJ、辺FJをひくとわかりやすい)
よって四角形EICFは一辺の長さ2√5のひし形であることが分かる。

問2 ①

問2 ①：線分EJの長さを求める問題です。
【・答え「(4√5)/5」】
三平方の定理よりEH2-EJ2=FH2-FJ2
EF=FH=2√5、FJ=-2√5-EJ、EH=4を上式に代入して 16-EJ2=20-(2√5-EJ)2
展開して整理すると、4√5EJ=16
これをといてEJ=(4√5)/5

問2 ②

問2 ②：立体BFGJの体積を求める問題です。
【・答え「16/5」】
立体BFGJは底面が△FGJ、高さが線分BFの三角錐である。
ここで⊿EFGについて、面積はFG×GH÷2=2×4÷2=4
△FGJと△EFGの面積比はFE:FJに等しく
FE=2√5-(4√5)/5=(6√5)/5、FJ=(4√5)/5
よって△EFGの面積をxとして4:x=2√5:(6√5)/5
これをといてx=12/5
よって立体BFGJの体積は12/5×4×1/3=16/5

【数学Ｃ】大問1：小問集合

小問集合とはいえ、どれも多少ひねった問題になっているので、誤答しないように注意が必要です。
大問２、３が難しいので、大問１は完問必須です。

問1：二次方程式

問1：ｘ＝５－２√３のときのｘ²ー１０ｘ＋２を計算する問題です。
【・答え　－１１】
式にｘ＝５－２√３を代入すると、
ｘ²ー１０ｘ＋２
→（５－２√3）²ー１０（５－２√３）＋２　()内の計算をする
＝２５－２０√３＋１２－５０＋２０√３＋２　同類項をまとめる
＝－１１
となる。

問2：連立方程式

問2：ｘ－ｙ＋１＝３ｘ＋７＝－２ｙを解き、ｘとｙの解を求める問題です。
【・答え　ｘ＝－５　ｙ＝４】
方針としては、

1. 分かりやすい連立方程式（○ｘ＋△ｙ＝◇）の形にする。
2. 連立方程式を解く

とするのが正攻法です。まず、
ｘ－ｙ＋１＝－２ｙ
３ｘ＋７＝－２ｙ
の二つに分けます。これを○ｘ＋△ｙ＝◇に変形すると、
ｘ＋ｙ＝－１　…①
３ｘ＋２ｙ＝－７　…②
となります。この連立方程式を解くと、
３ｘ＋３ｙ＝－３　…①×3
３ｘ＋２ｙ＝－７　…②
これを引き算すると、ｙ＝４。
これを①に代入すると、ｘ＝－５。
従って上記の答えになる。

問3：二次方程式

問3：（ａ＋２ｂ）²＋ａ＋２ｂ－２を因数分解する問題です。
【・答え　（ａ＋２ｂ＋２）（ａ＋２ｂ－１）】
これを展開してから再び因数分解すると大変な時間ロスになる。なので、まず共通した部分を探す。
この問題の場合はａ＋２ｂが共通部分として存在する。
これをｘとすると、ｘ²＋ｘ－２となる。これを因数分解すると、
（ｘ＋２）（ｘ－１）
ｘ＝ａ＋２ｂを代入すると、
（ａ＋２ｂ＋２）（ａ＋２ｂ－１）
となる。

問4：平方根の不等式

問4：√３１と８/√２と5.5の大小関係を正しく表している選択肢を選ぶ問題です。
【・答え　オ】
値を二乗すると、小さい大小関係の差が明確になるのでわかりやすい。（値の大小関係はそれぞれを二乗したり根をとっても変わらないため、それを利用する。）
（√３１）²＝３１
（８/√２）²＝６４/２＝３２
（５．５）²＝３０．２５
これより、大小関係は５．５＜√３１＜８/√２　とわかるので、正しい選択肢であるオを選ぶ。

問5：確率

問5：2つのサイコロＡ,Ｂを同時に投げ、出た目をそれぞれａ,ｂとするとき、２ｂ/ａが素数となる確率を求める問題です。
【・答え　１/４】
２ｂ/ａで存在しうる最大の数は１２となる。（ａ＝１、ｂ＝６のとき）
それ以下の素数は２，３，５，７，１１なので、この値となる確率を求める。
ａ＝１のとき：２，４，６，８，１０，１２→素数は２の１つ
ａ＝２のとき：１，２，３，４，５，６→素数は２，３，５の３つ
ａ＝３のとき：２/３，４/３，２，８/３，１０/３，４→素数は２の1つ
ａ＝４のとき：１/２，１，３/２，２，５/２,３→素数は２，３の2つ
ａ＝５のとき：２/５，４/５，６/５，８/５，２，１２/５→素数は２の1つ
ａ＝６のとき：１/３，２/３，１，４/３，５/３，２→素数は２の1つ
全ての通りを考えると、9通りあることが分かる。
従って、（２ｂ/ａが素数となる通り）/（すべての通り）＝９/３６＝１/４

問6：連立方程式

問6：黒と白の碁石が合わせて100個入っている袋から40個をランダムで取り出す操作を2回行い、その結果から袋全体の黒の碁石の数を推測する問題です。
【・答え　５６０】
一見すると確率の問題に見えるかもしれないが、これは連立方程式の問題である。
方針としては、

1. 情報を整理して立式する。
2. 式を解く

とするとよい。

最初の黒の碁石をＸ、白の碁石をＹとする。この状態で４０個の碁石を取り出した結果が黒：白＝３２：８となった。
この結果はあくまで４０個の碁石から取り出した結果ではあるが、これを全体の碁石の結果と推定する。
全体の黒白の比と結果の比を式で表すと
Ｘ：Ｙ＝３２：８＝４：１
となる。これを変形すると
４Ｙ＝Ｘ　…①
次に、白の碁石に１００個追加した上でもう一度４０個の碁石を取り出した結果が黒：白＝２８：１２となった。
この結果も全体の碁石の結果と推定する。ただし、今回は白の碁石が１００個追加されているので、比を式で表すと
Ｘ：Ｙ＋１００＝２８：１２＝７：３
となる。これを変形すると
７Ｙ＋７００＝３Ｘ　…②
となる。
この連立方程式を解くと、Ｘ＝５６０，Ｙ＝１４０
となる。したがって、答えは５６０。

問7：整数

問7：連続する二つの奇数ａ,ｂ(ａ＜ｂ)が「０＜ａ＜１００かつ０＜ｂ＜１００」「ｂ²ーａ²＝１００ｍ(ｍは自然数)」を同時に満たすときのａ,ｂを求める問題です。
【・答え　ａ＝４９、ｂ＝５１】
文字の数を減らし、問題を的確にとらえることが出来るかがポイントとなる。（１と９９、２と９８…と当たっていくのは方針としてはナシです！）

方針

1. 情報を整理して、減らせる文字は減らす
2. 計算する

解答
整理１：ａとｂの2つがあると、式が最低２つ無いと答えを絞ることが出来ない。
そこで、条件よりｂ＝ａ＋２とする。（ａより１つ大きい奇数がｂなので、ａより２大きい値がｂである。）
整理２：問題文より「ｂ²ーａ²＝１００ｍ（ｍは自然数）」という式を立てる。ｍの値によって１００、２００、３００…となる。そのいずれかが当てはまればＯＫである。

計算
ｂ＝ａ＋２とｂ²ーａ²＝１００ｍより、
（ａ＋２）²ーａ²＝１００ｍ
となる。これを計算すると、
ａ²＋４ａ＋４－ａ²＝１００ｍ
４ａ＋４＝１００ｍ
４で割ると
ａ＋１＝２５ｍ
となる。

ｍには１、２、３…が入るので、
ａ＋１＝２５
ａ＋１＝５０
ａ＋１＝７５
ａ＋１＝１００
…
となる。これらの式によってａとなる可能性の値は
２４、４９、７４、９９、１２４…

このうち、偶数と１００以上を除くと
４９、９９
が残る。
「ａ、ｂ＜１００」より、ａ＝９９はｂ＝１０１となってしまうので、９９は不適。
従って、ａ＝４９。
ｂ＝ａ＋２＝４９＋２＝５１。

問8：放物線

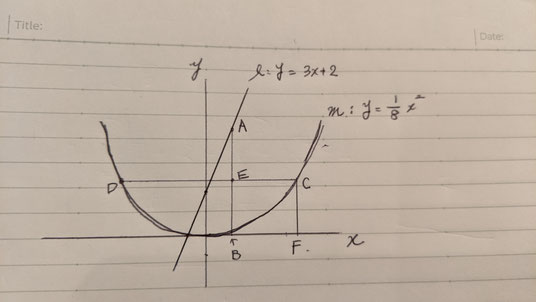
問8：ｙ＝３ｘ＋２上の点Ａと点Ｂ(ｘ軸上で点Aと同じｘ座標の点)を繋いだ線分ＡＢと、ｙ＝１/８ｘ²上の点Ｄと点Ｃを繋いだ線分DCの交点を点E、ｘ軸上にあり点Ｃと同じｘ座標の点を点Ｆとし、「ＤＥ＝ＡＢ」かつ「ＥＣ＝ＣＦ」であるときの点Aのｘ座標を求める問題です。
【・答え　√３】

方針
求めたいのは点Ａの座標であるｔの値である。ｔを用いてほかの座標を表し計算することで、ｔの値を求めることが出来る。

1. Ａ，Ｂの座標をtを用いて表し、ＡＢの長さを求める。
2. ＡＢの長さからＤＥの長さを求め、Ｄの座標が分かる。
3. Ｄの座標よりＣの座標が分かり、Ｆの座標が分かる。
4. ＥＣ＝ＣＦを表す
5. ｔの値を導出する

座標を求める
Ａ：３ｘ＋２のうえにあり、ｘ座標はｔなので、Ａ（ｔ，３ｔ＋２）
Ｂ：Ａと同じｘ座標でｘ軸上にあるので、Ｂ（ｔ，０）
したがって、ＡＢの長さは３ｔ＋２となる。

ＤＥ＝ＡＢなので、ＤＥの長さは３ｔ＋２
Ｅのｘ座標はＡ，Ｂと同じなのでｔ。したがって、Ｄのｘ座標は
ｔ－（３ｔ＋２）＝－２ｔ－２
Ｄは１/８ｘ²上の点なので、Ｄ（－２ｔ－２，（４ｔ²＋８ｔ＋４）/８）
Ｅのｙ座標はＤと等しいので、Ｅ（ｔ，（４ｔ²＋８ｔ＋４）/８）

Ｄとｙ軸に対して線対称の位置にあるＣ座標は、Ｄ座標のｘ軸の符号が変わるだけなので、Ｃ（２ｔ＋２，（４ｔ²＋８ｔ＋４）/８）
Ｆの座標はＣとｘ座標が同じで、ｘ軸上にあるので、Ｆ（２ｔ＋２、０）

ＥＣとＣＦを求める
ＥとＣはｙ座標が同じなので、ＥＣの長さはｘ座標の差からわかる。ｘ座標の値が大きいＣからＥを引くと、
２ｔ＋２－ｔ＝ｔ＋２＝ＥＣ

ＣとＦはｘ座標が同じなので、ＣＦの長さはｙ座標の差からわかる。ｙ座標の値が大きいＣからＦを引くと、
（４ｔ²＋８ｔ＋４）/８ー０＝（４ｔ²＋８ｔ＋４）/８＝ＣＦ

ｔを求める
ＥＣ＝ＣＦよりｔを求める。
ｔ＋２＝（４ｔ²＋８ｔ＋４）/８
４ｔ²＋８ｔ＋４＝８ｔ＋１６
４ｔ²ー１２＝０
４（ｔ²ー３）＝０
（ｔー√３）（ｔ＋√３）＝０
ｔは正の数なので、ｔ＝√３は不適。従って、ｔ＝√３となる。

大問2：平面図形

平面図形の問題です。相似の関係を見つけられるかがポイントです。
証明問題については、相似条件と示す方法を分かりやすく記述出来るように勉強しておきましょう。
数学C全体を見ると、大問２までは完問を目指したいです。

問1

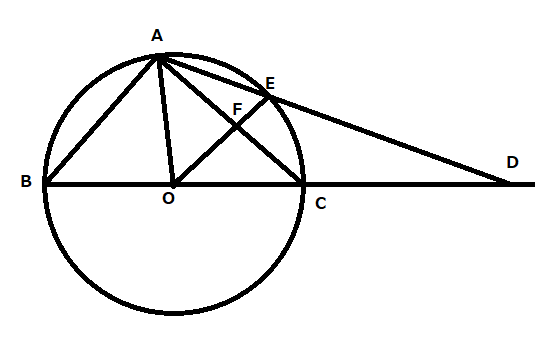
問1：∠ＡＯＢの大きさをａ°とするときの弧ＡＢの長さをａを用いて表す問題です。
【・答え　πａ/４５】
弧の長さは中心角ａ°と半径からから求めることが出来る。
円周は２πｒで求められ、８πである。

その円周に占める弧はａ/３６０で示されるので、弧ABの長さは
８π×ａ/３６０＝πａ/４５
となる。

問2

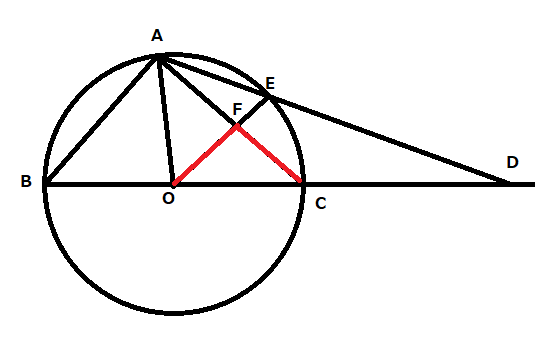
問2：ＦＯ＝ＦＣを証明する問題です。
一つの弧に対する中心角の大きさは、その弧に対する円周角の大きさの２倍なので、
∠ＦＯＣ＝２∠ＣＡＥ　…①
△ＣＤＡはＣＤ＝ＣＡより二等辺三角形なので、
∠ＣＤＡ＝∠ＣＡＥ　…②
∠ＦＣＯは△ＣＤＡの頂点における外角なので
∠ＦＣＯ＝∠ＣＤＡ＋∠ＣＡＥ　…③
②、③より∠ＦＣＯ＝２∠ＣＡＥ　…④
①、④より∠ＦＯＣ＝∠ＦＣＯ
従って、△ＦＯＣは二等辺三角形なので、
ＦＯ＝ＦＣとなる。

問3

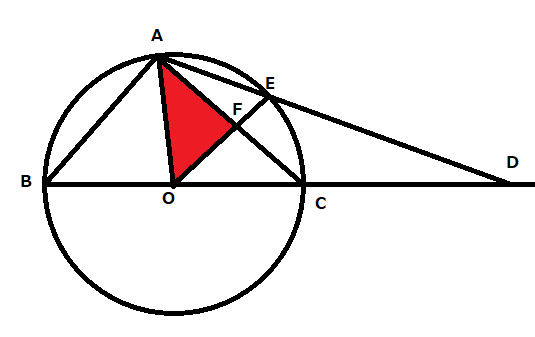
問3 ①：ＡＣ＝６cmであるとき線分ＦＣの長さを求める問題です。
【・答え　８/３】
△ＦＯＣと△ＯＣＡの相似から、辺の長さを求めていく。
まず、同じ角度を共有しているので
∠ＯＣＡ＝∠ＦＣＯ　…①
△ＯＣＡはＯＣ＝ＯＡの二等辺三角形なので∠ＯＣＡ＝∠ＯＡＣ　…②
△ＦＯＣはＦＯ＝ＦＣの二等辺三角形なので∠ＦＣＯ＝∠ＦＯＣ　…③
①，②，③より∠ＯＡＣ＝∠ＦＯＣ　…④
①と④より２つの角が等しいので、
△ＦＯＣと△ＯＣＡは相似であると分かる。

さて、ＯＡ：ＡＣ＝ＦＣ：ＯＣ
の関係からＦＣの長さを導出する。
それぞれに長さを代入して計算すると、
４：６＝ＦＣ：４
６×ＦＣ＝１６
ＦＣ＝８/３
したがって、ＦＣ＝８/３

問3 ②：ＡＣ＝６cmであるとき△ＡＯＦの面積を求める問題です。
【・答え　５√７/３】

△ＡＯＦ＝△ＯＡＣ－△ＦＣＯより求める。
△ＯＡＣの面積
まず△ＯＡＣの点ＯからＡＣと垂直に下したときに重なる点を点Ｇとおく。
ＯＡ＝４、ＡＧ＝３
であり、ＯＧは三平方の定理より
１６－９＝７
よってＯＧ＝√７
△ＯＡＣの面積は
√７×６÷２
＝３√７

△ＦＯＣの面積
まず△ＦＯＣの点ＦからＯＣと垂直に下したときに重なる点を点Ｈとおく。
ＦＯ＝８/３、ＯＨ＝２
より、ＦＨは三平方の定理を用いて
６４/３－４＝２８/９
よってＯＧ＝２√７/３
△ＦＯＣの面積は
４×２√７/３÷２
＝４√７/３

△ＡＯＦの面積は
△ＯＡＣ－△ＦＯＣ＝３√７－４√７/３
＝５√７/３

大問3：立体図形

錐体の問題です。問１①、②や問２①は確実に解けるようにしておく必要があると思います。
問2の②は特に難しいです。過去問の傾向からすると易ですが、それでも似たような問題を複数解いて慣れることが必要かもしれません。

問1 ①

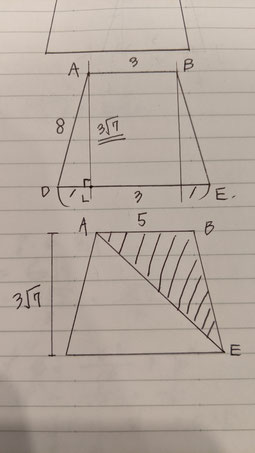
問1 ①：△AEBの面積を求める問題です。
【・答え　９√７/２ （ｃｍ²）】（解説では単位を省略します。）
まず、四角形ADEBの高さにあたる長さを求めたい。
ABとDEが平行であり、ABとBEが同じ長さであることから、AからDEに下した垂線とDEの交点をLとすると、DL＝１とわかる。
ALの長さを求めるために三平方の定理を用いると、
（８）²＝１²＋AL²
AL＝√６３＝３√７
この長さを用いて△AEBを求めると、
AB×AL÷２→３×３√７÷２
＝９√７/２

したがって、△AEBの面積は９√７/２となる。

問1 ②

問1 ②：線分AHの長さを求める問題です。
【・答え　２４/５（ｃｍ）】（解説では単位を省略します。）
△ADEと△HDGが相似であることがわかれば、比より長さを求めることが出来る。
△ADEと△HDGが相似である証明
同じ角であるから∠ADE＝∠HDG　…①
AE//HGより∠DEA＝∠DGH　…②
①、②より△ADEと△HDGはそれぞれ二つの角が等しいので
△ADE∽△HDG

次にHDの長さを求めていく。
AD：DE＝HD：DG
でもとめられる。
DG＝DE－GE＝５－３＝２であるから、
８：５＝HD：２
HD＝１６/５

求めたいのはAHなので、
AH＝AD－HD＝８－１６/５
AH＝２４/５

したがって、AHの長さは２４/５である。

問1 ③

問1 ③：線分IHの長さを求める問題です。
【・答え　３√１５/５（ｃｍ）】
DからACに下した垂線のACの交点をNとする。NDの長さが分かれば、図形の比よりIHを求められる。
△ACDの面積を求めていく。AからCDに下した垂線のCDとの交点をA’とすると、AA’の長さは三平方の定理より
（AC）²＝（CA’）²＋（AA’）²
AA’＝２√１５
とわかる。したがって、△ACDの面積は
△ACD=CD×AA’÷２
＝４×２√１５÷２
＝４√１５
とわかる。

次に△ACDの面積をACを底辺、NDを高さとして求める式を立ててみる。△ACDの面積は上で求めたので、
AC×ND÷２＝８×ND÷２＝４√１５
ND＝√１５
とわかる。

NDとIHの長さの関係は、△ANDと△AIHが相似であることと、AH：ADが３：５の関係であることから、(前問参照)
AH：AD＝IH：ND
３：５＝IH：√１５
IH＝３√１５/５
したがって、IHの長さは３√１５/５である。

問2 ①

問2 ①：線分JKの長さを求める問題です。
【・答え　７/２（ｃｍ）】
問1①と同じ手法で解くことが出来る。

ALとJKの交点をMとおく。ここで出来る△AJMと△ADLは相似の関係となっている(証明省略)。
そこで、AJ：JM＝AD：DLとすると、
２：JM＝８：１
より、JM＝１/４とわかる。
次に、BからDEにひいた垂線とDEの交点をO、JKとの交点をPとおく。
AB//JK、AJ＝BKより、同様のことが言えるので、PK=１/４となる。
また、AM⊥JK、BP⊥JKよりMP＝ABとわかる。

従って、JK=JM＋MP＋PK＝１/４＋３＋１/４
JK＝７/２

問2 ②

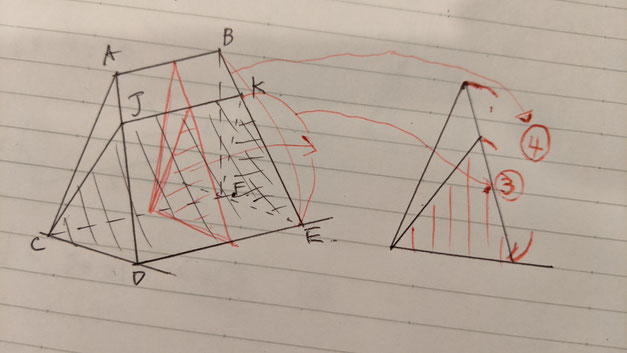
問2 ②：立体JK-CDEFの体積を求める問題です。
【・答え　２７√５９/４（ｃｍ³）】

まず、立体断面①の面積を求めていく。
底辺の長さはCDと同じなので４、斜辺は（１）で求めたALと同じなので、３√７
これより、まず高さ（ｘとする）を求めていく。
三平方の定理より、
（CD/２）²＋ｘ²＝（AL）²
４＋ｘ²＝６３
ｘ＝√５９
とわかる。したがって、①の面積は
４×√５９÷２＝２√５９
となる。

次に、求めたい体積部分の断面積を求める。
AD＝８、JD＝６と分かっていることから、①の面積と、そのうち求めたい体積部分の断面積の比は４：３と表せる。
従って、求めたい体積部分の断面積は
２√５９×３/４
＝３√５９/２
となる。

さて、立体JK-CDEFの体積の高さはJKとCFとDEの平均とすればいいので、
（JK＋CF＋DE）/３＝（７/２＋５＋５）/３＝９/２
となる。
したがって、体積は
体積＝断面積×高さ＝３√５９/２×９/２
＝２７√５９/４

 大阪府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。