大阪府の2020年3月実施の令和2年度（2020年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

大阪府の数学問題は、レベル別にＡＢＣの問題が用意されています。受験する学校によりどの問題を採用するかが異なります。
難易度は、Ａが易、Ｂがやや難、Ｃが難となっています。レベル差が顕著なので、各問題に対応する対策をとる必要があります。

 【大阪府】令和2年度一般入学者選抜の過去問はこちらから
数学Ａの過去問題はこちら＞＞
数学Ｂの過去問題はこちら＞＞
数学Ｃの過去問題はこちら＞＞

 大阪府の公立高校入試情報はこちら

【数学A】大問1：小問集合

問1：正負の数

問1：正負の数の計算をする問題です。
【・答え　ー１７】
－７－１０＝－１７

問2：正負の数

問2：正負の数の計算をする問題です。
【・答え　ー２/７】
÷〇　→　×１/〇　に変換する。
８/７÷（－４）＝８/７×（ー１/４）＝－２/７

問3：正負の数

問3：正負の数の計算をする問題です。
【・答え　１２】
３×（－２）²＝３×４＝１２

問4：文字と式

問4：文字と式の計算をする問題です。
【・答え　6ｘ-１１】
一旦バラした後、同じ文字・次数同士で計算する。
ｘ＋４＋５（ｘ－３）＝ｘ＋４＋５ｘ－１５＝６ｘ－１１

問5：文字と式

問5：文字と式の計算をする問題です。
【・答え　２ｘｙ²】
同じ文字同士のかけ算は次数を付けることで表す。
ｘｙ×２ｙ＝２ｘｙ²

問6：平方根

問6：平方根を含む式を計算する問題です。
【・答え　８√５】
平方根の中身を素因数分解して、根の値を合わせると計算できる。
√４５＋５√５＝３√５＋５√５＝８√５

大問2：小問集合

問1：式と代入

問1：ａ＝ー８のときの２ａ＋７を求める問題です。
【・答え　ー９】
ａにー８を代入する。
２×（－８）＋７＝－９

問2：正負の数

問2：表を読み、A市の気温がB市の気温より何℃高いかを求める問題です。
【・答え　５．９℃】
Ａ市は４．６℃、Ｂ市はー１．３℃である。４．６は０より４．６だけ大きい値であり、０は－１．３より１．３大きい値であるから、以下のように計算できる。
４．６＋１．３＝５．９
従って、A市はＢ市よりも５．９℃高い

問3：比例

問3：選択肢のうち、比例の関係であるものを選ぶ問題です。
【・答え　エ】
比例かどうかを見分けるためには、
・片方の値が増えたときに、もう一方の値が増えること　①
・もともとの値が０であること（ｘ＝０のときｙ＝０であること）　②
が両方満たされればよい。
ア：ビスケット０個の時点で３０ｇの重さがあるので、②を満たさない。
イ：早く進むほど（ｘの値が増えるほど）、かかる時間は短くなる（ｙの値が減る）ので、①を満たさない。
ウ：早く燃えるほど（ｘの値が増えるほど）、残りの線香の長さが短くなる（ｙの値が減る）ので、①を満たさない。
エ：①、②どちらも満たす。

問4：連立方程式

連立方程式　５ｘ＋ｙ＝２２　ｘ－ｙ＝ー４　についてｘとｙを解く問題です。
【・答え　ｘ＝３，ｙ＝７】
５ｘ＋ｙ＝２２を①、ｘ－ｙ＝－４を②とする。
②をｘ＝の形に変形すると、
ｘ＝ｙ－４
これを①に代入すると、
５ｘ＋ｙ＝２２　
→５（ｙ－４）＋ｙ＝２２
５ｙ－２０＋ｙ＝２２
６ｙ＝４２
ｙ＝７

ｙ＝７を②に代入すると、
ｘ－ｙ＝－４
→ｘ－７＝－４
ｘ＝３

問5：二次方程式

問5：二次方程式を解く問題です。
【・答え　ｘ＝ー５，ｘ＝２】
因数分解する。どのように分ければいいか分からない人は、－１０をいくつかのかけ算で表現する方法を考えるとよい。
それでも分からない人は解の公式を解ける。
ｘ²＋３ｘ－１０＝０
（ｘ＋５）（ｘ－２）＝０
ｘ＝－５,ｘ＝２

問6：確率

問6：二つのさいころの目の和が８になる確率を求める問題です。
【・答え　５/３６】
サイコロの目の和が８になるのは
（２,６）（３,５）（４,４）（５,３）（６,２）
の５通りである。一方、サイコロの目は全部で
６×６＝３６
の３６通りであるから、その確率は
５/３６となる。

問7：資料の読み取り

問7：選択肢のうち、資料から読み取れるものとして正しいものを選ぶ問題です。
【・答え　ウ】
冷静に資料を読み取れば、確実に得点できる問題である。
ア：１年生は1人、２年生は０人なので、この選択肢は誤り。
イ：１年生は６本～９本なので、範囲は４本である。２年生は５本～１０本なので、範囲は６本である。したがって、この選択肢は誤り。
ウ：１年生は少ない本数から数えていくと、５人目（中央値）は７本である。２年生は少ない本数から数えていくと、６人目（中央値）は７本である。したがって、この選択肢は正しい。
エ：１年生の最頻値は７本である。２年生の最頻値は８本である。したがって、この選択肢は誤り。

問8：二次関数

問8：二次関数について座標と変域を求める問題です。
【・答え　①：８　②㋐：0　㋑：９/２】
①ｙ＝ｘ²/２のグラフ上であり、ｘの値が－４のときのｙの値は、
ｙ＝ｘ²/２　→　ｙ＝（－４）²/２＝１６/２＝８
よって、ｙ＝８である。
②変域を求める。図を書くと一目瞭然である。
したがって、変域は　０≦ｙ≦８　である。

問9：展開図

問9：直方体の展開図について、平行面・体積を求める問題です。
【・答え　①：イ　②：５ａ²】
②：面かを底面とした直方体を考える。面かの一辺の長さはａｃｍなので、面積はａ×ａ＝ａ²ｃｍ²
面かを底面、辺ＡＢを高さとすると、直方体の体積は５×ａ²＝５ａ²ｃｍ³である。

大問3：一次関数

スライドショーで表示される写真の枚数と、スライドショー全体の時間について考える問題です。スライドショーのタイトルを４秒間表示し、その後1枚につき５秒間表示することにしたそうです。写真の枚数をｘ枚、スライドショーの時間をｙ秒としたとき、次の3問を解いていきます。

問1：一次関数

問1：ｘとｙの関係を表した表の空欄を埋める問題です。
【・答え　ア：２４　イ：３９】
ｘ＝４のときは、４枚分の時間（４×５＝２０秒）とタイトル（４秒）があるので、スライドショーの時間は
２０＋４＝２４（秒）である。
ｘ＝７のときは、７枚分の時間（７×５＝３５秒）とタイトル（４秒）があるので、スライドショーの時間は
３５＋４＝３９（秒）である。

問2：一次関数

問2：ｙをｘの式で表す問題です。
【・答え　５ｘ＋４】
問1より、スライドショーの時間は枚数に応じて増えていく時間と、枚数によらず変わらない（タイトルの）時間の足し合わせであるとわかる。したがって、
（スライドショーの時間）＝（写真の時間）×（写真の枚数）＋（タイトルの時間）
と表せる。これを文字式に置き換えると
ｙ＝５ｘ＋４
となる。

問3：一次関数

問3：ｙ＝８４となるときのｘの値を求める問題です。
【・答え　１６】
問2で求めた式にｙ＝８４を代入すれば求められる。
ｙ＝５ｘ＋４　→　８４＝５ｘ＋４
５ｘ＝８０
ｘ＝１６

大問4：平面図形

次のような図形があるとき、次の問いに答えていく大問です。

問1：対角線の長さ

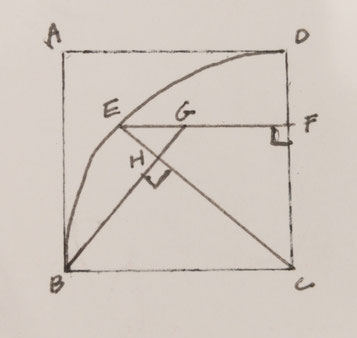
問1：正方形ABCDの対角線ACの長さを求める問題です。
【・答え　９√２】
正方形の対角線は正方形の辺との比で簡単に求められる。
正方形の辺：正方形の対角線＝１：√２
より、正方形ＡＢＣＤの対角線の長さをｘ(ｃｍ)とすると
９：ｘ＝１：√２
ｘ＝９√２

問2：面積

問2：おうぎ形CDBの面積を求める問題です。
【・答え　８１π/４】
おうぎ形の面積は、円が欠けたものと考えれば簡単に求められる。
辺ＣＤ（辺ＣＢ）の長さは９(ｃｍ)であり、それを半径とした円の面積は（半径）²πで求められるので、
面積＝９²π＝８１πとなる。
問題のおうぎ形はその円の１/４（９０°/３６０°）の面積なので、
８１π/４(ｃｍ)

問3：証明

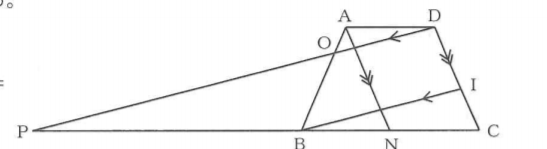
問3：問題中に示された「△CHB≡△EFC」の証明の空欄ⓐⓑに適している「辺・角を表す文字」をそれぞれ答える問題です。また、空欄Ⓒに適した選択肢を選ぶ問題です。
【・答え　ⓐ：CE　ⓑ：CEF　Ⓒ：イ】
ⓐ：△ＥＦＣのうち、辺ＣＥはおうぎ形の半径を構成している。
ⓑ：相似であることを利用して、∠ＢＣＨ＝∠ＣＥＦを導く。
Ⓒ：い　の条件で直角三角形を示し、あとう　の条件で斜辺と鋭角が対応していることを示している。

問4：平面図形

問4：EF＝７ｃｍであるときの線分ＧＦの長さを求める問題です。
【・答え　３１/７】
△ＣＨＢと△ＥＦＣの相似関係と、問３で示した△ＣＨＢと△ＥＦＣの合同関係を利用する。
最終的にはＧＦ＝ＥＦ－ＥＧで求める。

△ＣＨＢ≡△ＥＦＣより、ＥＦ＝ＣＨ＝７(ｃｍ)
ＥＨ＝ＣＥ－ＣＨなので、９－７＝２(ｃｍ)
△ＣＨＢ∽△ＥＦＣより、
ＣＨ：ＣＢ＝ＥＨ：ＥＧ
７：９＝２：ＥＧ
ＥＧ＝１８/７
とわかる。

これをＧＦ＝ＥＦ－ＥＧに代入すると、
ＧＦ＝７－１８/７＝（４９－１８）/７＝３１/７(ｃｍ)

【数学B】大問1：小問集合

問1：正負の数

問1：１８÷（ー６）＋（ー５）²を計算する問題です。
【・答え　２２】
累乗を計算　→　乗除を計算　→加減を計算する。
１８÷（－６）＋（－５）²
＝１８÷（－６）＋２５
＝－３＋２５
＝２２

問2：文字と式

問2：（ａー１）/２＋（ａ＋７）/４を計算する問題です。
【・答え　３ａ＋５/４】
分母を大きい方に揃えて、分子を計算する。
（ａー１）/２＋（ａ＋７）/４
＝２（ａー１）/４＋（ａ＋７）/４
＝（２ａー２＋ａ＋７）/４
＝３ａ＋５/４

問3：文字と式

問3：２ａ²÷ａｂ×（ー５ｂ²）を計算する問題です。
【・答え　ー１０ａｂ】
数字と文字をそれぞれ計算する。（÷〇　→　×１/〇に変換してもよい）
２ａ²÷ａｂ×（ー５ｂ²）
＝２ａ²×（１/ａｂ）×（－５ｂ²）
＝－１０ａｂ

問4：文字と式

問4：（ｘ＋２）²ーｘ（ｘ－３）を計算する問題です。
【・答え　７ｘ＋４】
一旦展開　→　文字と数をそれぞれまとめる。
（ｘ＋２）²ーｘ（ｘ－３）
＝ｘ²＋４ｘ＋４－ｘ²＋３ｘ　…ｘ²が消える
＝７ｘ＋４

問5：正負の数

問5：ａが０でないとき、その値の符号がつねにａの符号と同じであるものをすべて選ぶ問題です。
【・答え　エ，オ】
ア：符号が常に逆になるので、誤り。
イ：ａがー１のときａ＋２は１となり符号が逆になる。したがって、誤り。
ウ：ａが負の数の時、ａ²は正の値となる。したがって、誤り。
エ：正しい。
オ：正しい。

問6：平方根

問6：√１８９ｎ　（ｎは自然数）の値が自然数となるような最も小さいｎの値を求める問題です。
【・答え　２１】
平方根を素因数分解　→　対でないものをｎで対にすることで自然数となる。
１８９＝３³×７＝３²×２１
したがって、ｎ＝２１
（√１８９×２１＝√３⁴×７²＝６３）

問7：表の読み取り

問7：表中のｘの値を求める問題です。
【・答え　２．５】
（３．６＋４．０＋ｘ）/３
と求めるのは誤りである。(それぞれの平均の重みを考慮していない為)
全員が詠んだ本の冊数/全員の人数＝平均　であることに立ち戻る。
各学年の詠んだ本の冊数は（読んだ本の冊数の平均値）×（部員の人数）で求められるから、
１年生の読んだ本の冊数＝３．６×２０＝７２(冊)
２年生の読んだ本の冊数＝４．０×１２＝４８(冊)
３年生の読んだ本の冊数＝ｘ×８＝８ｘ(冊)

これを全部足したものが（全員が読んだ本の冊数）であるから、
７２＋４８＋８ｘ＝１２０＋８ｘ(冊)
となる。これを４０人で割ったときの平均が３．５冊となるので
（１２０＋８ｘ）/４０＝３．５
と立式できる、これを解くと
１２０＋８ｘ＝１４０
８ｘ＝２０
ｘ＝２．５(冊)

問8：確率

問8：2つのさいころＡ，Ｂを同時に投げた時の目をａ，ｂとしたときの１０ａ＋ｂの値が８の倍数である確率を求める問題です。
【・答え　５/３６】
ａとｂが６のときの１０ａ＋ｂの値は６６である。したがって、６６以下の８の倍数を考えると、
８，１６，２４，３２，４０，４８，５６，６４
があり、これを満たす通りを数えると５通りある。
一方、サイコロの出目は３６通りなので、確率は５/３６となる。

問9：二次関数

問9：次のグラフｙ＝ａｘ²（ａは正の定数）のａの値を求める問題です。
【・答え　３/１４】

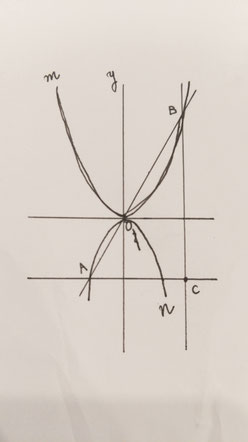
方針

1. Ａの座標とＣの座標によってＢの座標を特定する。
2. Ｂの座標を通る二次関数が定まる。
3. ａを求める。

ＡとＣのｙ座標は同じなので、Ａのｙ座標はー６とわかる。
ｎ：ｙ＝－３ｘ²/８はＡの座標を通るので、ｙにー６を代入するとＡのｘ座標が求まる。
－６＝－３ｘ²/８
ｘ＝４、－４と求められる。問よりＡのｘ座標は負であるとあるので、ｘ＝－４
Ａの座標は（－４,－６）と分かる。

次に、原点とＡの座標を通る直線の式（…①）は
ｙ＝３ｘ/２
と分かる。この直線とＣのｘ座標（ｘ＝７）が交わる点がＢとなるので、①にｘ＝７を代入すると、
ｙ＝３×７/２＝２１/２
と分かるので、Ｂの座標は（７,２１/２）と分かる。

これをｍ：ｙ＝ａｘ²に代入する。
２１/２＝ａ×７²＝４９ａ
ａ＝２１/(２×４９)
ａ＝３/１４

大問2：一次関数

スライドショーで表示される写真の枚数と、スライドショー全体の時間について考える問題です。流す写真は「体育祭」と「文化祭」に分かれており、前半に体育祭の写真、後半に文化祭の写真が流れるようにするそうです。
【体育祭】スライドショーのタイトルを４秒間表示し、その後1枚につき５秒間表示する。
【文化祭】スライドショーのタイトルを４秒間表示し、その後1枚につき８秒間表示する。
これらの条件のもと、次の問いに答えていく大問です。

問1 ①：一次関数

問1 ①：ｘとｙの関係を表した表の空欄を埋める問題です。
【・答え　ア：２４　イ：３９】

ｘ＝４のときは、４枚分の時間（４×５＝２０秒）とタイトル（４秒）があるので、体育祭のスライドショーの時間は
２０＋４＝２４（秒）である。
ｘ＝７のときは、７枚分の時間（７×５＝３５秒）とタイトル（４秒）があるので、体育祭のスライドショーの時間は
３５＋４＝３９（秒）である。

問1 ②：一次関数

問1 ②：ｙをｘの式で表す問題です。
【・答え　５ｘ＋４】
問1 ①より、体育祭のスライドショーの時間は枚数に応じて増えていく時間と、枚数によらず変わらない（タイトルの）時間の足し合わせであるとわかる。したがって、
（スライドショーの時間）＝（写真の時間）×（写真の枚数）＋（タイトルの時間）
と表せる。これを文字式に置き換えると
ｙ＝５ｘ＋４
となる。

問1 ③：一次関数

問1 ③：ｙ＝８４となるときのｘの値を求める問題です。
【・答え　１６】

問1 ②で求めた式にｙ＝８４を代入すれば求められる。
ｙ＝５ｘ＋４　→　８４＝５ｘ＋４
５ｘ＝８０
ｘ＝１６

問2：連立方程式

問2：体育祭の写真の枚数をｓ，文化祭の写真の枚数をｔとし、その枚数の合計が５０枚、全体の時間が３００秒であるときのｓとｔの値を求める問題です。
【・答え　ｓ＝３６　ｔ＝１４】
２つの式を作り、連立させて解いていく。
１：体育祭と文化祭の写真の枚数が５０枚である。
２：体育祭のスライドショーの時間と文化祭のスライドショーの時間を３００秒である。
の2つが分かっているので、これらをそれぞれ立式する。

体育祭の写真の枚数（ｓ）＋文化祭の写真の枚数（ｔ）＝５０(枚)より
ｓ＋ｔ＝５０　…①

体育祭のスライドショーの時間＋文化祭のスライドショーの時間＝３００(秒)であり、
５ｓ＋４＋８ｔ＋４＝３００
５ｓ＋８ｔ＝２９２　…②

①と②を連立して解く。

①を変形して、
ｓ＝５０－ｔ
これを②に代入すると、
５（５０－ｔ）＋８ｔ＝２９２
２５０－５ｔ＋８ｔ＝２９２
３ｔ＝４２
ｔ＝１４

ｔ＝１４を①に代入すると、
ｓ＋１４＝５０
ｓ＝３６

大問3：平面図形

問1 ①：線分の長さ

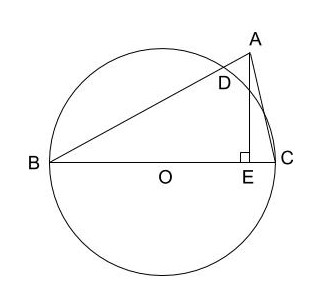
問1 ①：線分BEの長さを求める問題です。
【・答え　３√３】
∠ＡＢＣ＝３０°、∠ＢＥＡ＝９０°ということは、線分ＡＢ：線分ＢＥ：線分ＡＥが２：√３：１であるとわかる（３０°６０°の角を持つ直角三角形の辺の比より）。
よって、ＡＢ：ＢＥ＝６：ＢＥ＝２：√３
ＢＥ＝３√３

問1 ②：弧の長さ

問1 ②：弧BDの長さを求める問題です。
【・答え　２π】
ＯＤに線を引く。
∠ＯＢＤ＝∠ＯＤＢ＝３０°であるから、∠ＢＯＤ＝１２０°とわかる。
従って、円周×１/３（１２０°/３６０°）すればいいので、
円周×１/３＝６π×１/３＝２π
したがって、弧ＢＤの長さは２πである。

問2 ①：証明

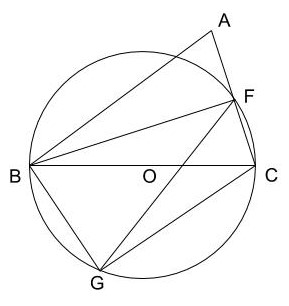
問2 ①：△ABCと△BFGが相似であることを証明する問題です。
【・証明
△ABCと△BFGにおいて、
同じ弧に対する円周角は等しいから、∠ACB＝∠BGF　…①
ABとCGは平行であり、平行線の錯角は等しいから、∠ABC＝∠BCG　…②
同じ弧に対する円周角は等しいから、∠BFG＝∠BCG　…③
②、③より、∠ABC＝∠BGF　…④
①、④より、二組の核がそれぞれ等しいから、△ABCと△BFGは相似である。
】

問2 ② ㋐：線分の長さ

問2 ② ㋐：ＦＣ＝２ｃｍのときの線分ＢＧの長さを求める問題です。
【・答え　８√２/３】
問2 ①で証明した△ＡＢＣ∽△ＢＦＧより、ＡＣ：ＢＧ＝ＡＢ：ＢＦ（…(ⅰ)）が言えるので、ＡＣ、ＢＦを求めることでＢＧを導く。
△ＢＦＣは直角であり、△ＡＢＣは二等辺三角形なので、Ｆは線分ＡＣの中点であるとわかる。したがって、
ＡＣ＝ＦＣ×２＝４(ｃｍ)

ＢＦは三平方の定理で求められる。
ＡＦ＝２(ｃｍ)、ＡＢ＝６(ｃｍ)なので、
ＢＦ²＝ＡＢ²ーＡＦ²
ＢＦ²＝３６－４
ＢＦ²＝３２
ＢＦ＝４√２

(ⅰ)についてＢＧ以外が分かったので、求めていく。
４：ＢＧ＝６：４√２
６ＢＧ＝１６√２
ＢＧ＝８√２/３

問2 ② ㋑：面積

問2 ② ㋑：ＦＣ＝２ｃｍのときの△ＦＧＣの面積を求める問題です。
【・答え　２８√２/９】
（△ＦＣＧの面積）＝（△ＢＦＣの面積）＋（△ＢＧＣの面積）－（△ＢＦＧの面積）で求められる。

△ＢＦＣの面積＝ＢＦ×ＦＣ÷２＝４√２×２÷２＝４√２(ｃｍ²)
△ＢＧＣの面積＝ＢＧ×ＧＣ÷２
ＧＣは三平方の定理で求めることができるので、
ＧＣ²＝ＢＣ²ーＢＧ²

ＧＣ＝１４/３
よって、
△ＢＧＣの面積＝８√２/３×１4/３÷２＝５６√２/９(ｃｍ²)

△ＢＦＧの面積はＢＧ×高さ÷２で求められる。
（高さ）²＝ＢＦ²－（ＢＧ/２）²
＝（４√２）²－（４√２/３）²
＝３２－３２/９
＝２５６/９
高さ＝１６/３(ｃｍ)

より、△ＢＦＧの面積は
△ＢＦＧの面積＝８√２/３×１６/３÷２
＝６４√２/９(ｃｍ³)

最後にこれらを計算する。
（△ＦＣＧの面積）＝（△ＢＦＣの面積）＋（△ＢＧＣの面積）－（△ＢＦＧの面積）
＝４√２＋５６√２/９ー６４√２/９
＝２８√２/９(ｃｍ³)

大問4：立体図形

次のような図形があるとき、次の問いに答えていく大問です。

問1 ①：平行面

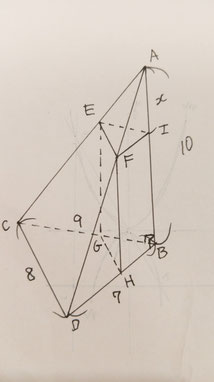
問1 ①：次の選択肢のうち、線分ＦＩと平行な面であるものを選ぶ問題です。
【・答え　ウ】
それぞれの選択肢を延長したときに、交わらないのは面ＢＣＤのみである。

問1 ②：線分の長さ

問1 ②：四角形EGHFの面積が１６ｃｍ²であるときのＡＩの長さ（ｘ）を求める問題です。
【・答え　５－√５】
四角形ＥＧＨＦの面積はＥＦ×ＦＨで求められる。
ＦＨ＝ＢＩであり、ＢＩ＝ＡＢ－ＡＩで求められるので、
ＦＨ＝１０－ｘ

△ＥＦＩと△ＣＤＢは相似の関係にあるので、ＥＦは
ＥＦ：ＡＩ＝ＣＤ：ＡＢより
ＥＦ：ｘ＝８：１０
ＥＦ＝４ｘ/５

四角形ＥＧＨＦの面積が１６(ｃｍ²)となるので、
（１０－ｘ）×４ｘ/５＝１６
これを変形して、
ｘ²－１０ｘ＋２０＝０
ｘについて解くと、
ｘ＝５－√５、５＋√５
設問より０＜ｘ＜５なので、
ｘ＝５－√５

問2 ①：線分の長さ

問2 ①：線分ＢＪの長さを求める問題です。
【・答え　３√５】
ＤＪの長さをｙとする。
△ＢＪＤについて、ＢＪ²を三平方の定理より解くと、
ＢＪ²＝ＢＤ²－ｙ²＝４９－ｙ²　…①
また、△ＢＪＣについて、ＢＪ²を三平方の定理より解くと、
ＢＪ²＝ＢＣ²－ＣＪ²＝ＢＣ²－（ＣＤ－ＤＪ）²＝８１－（８－ｙ）²　…②

①②について方程式を解くと、
４９－ｙ²＝８１－（８－ｙ）²
ｙ＝２

これを①に代入してＢＪを求めると、
ＢＪ²＝４９－４＝４５
ＢＪ＝３√５

問2 ②：体積

問2 ②：立体ＥＦＬーＣＤＫの体積を求める問題です。
【・答え　４９√５/２】
方針：立体Ａ－ＣＤＫから立体Ａ－ＥＦＬの体積を引
設問より、立体Ａ－ＣＤＫと立体Ａ－ＥＦＬは相似であり、その相似比はＡＣ：ＡＥ＝２：１より、
体積比は８：１であるとわかる。

立体Ａ－ＣＤＫの体積は立体Ａ－ＢＣＤからＫ－ＢＣＤを引くと求めれらる。
立体Ａ－ＢＣＤ＝ＡＢ×△ＢＣＤ×１/３＝ＡＢ×ＢＪ×ＣＤ×１/２×１/３
＝１０×３√５×８×１/６
＝４０√５
立体Ｋ－ＢＣＤ＝ＫＢ×△ＢＣＤ×１/３＝ＫＢ×ＢＪ×ＣＤ×１/２×１/３
＝３×３√５×８×１/６
＝１２√５

したがって、立体Ａ－ＣＤＫの体積は
４０√５－１２√５＝２８√５

求めたい立体ＥＦＬーＣＤＫの体積は、
立体Ａ－ＣＤＫ×７/８＝２８√５×７/８
=４９√５/２

【数学C】大問1：小問集合

問1：文字と式

問1：３ａ²ｂ/８÷９ａｂ²/４×（－３ｂ）²を計算する問題です。
【・答え　３ａｂ/２】
÷〇　→　×1/〇にする。
３ａ²ｂ/８÷９ａｂ²/４×（－３ｂ）²
＝３ａ²ｂ/８×４/（９ａｂ²）×９ｂ²
＝３ａ²ｂ×４×９ｂ²/８×９ａｂ²
＝３ａｂ/２

問2：平行根

問2：６－√１８/√２＋√２（１＋√３）（１－√３）を計算する問題です。
【・答え　ー３＋√２】
有理化・展開によって簡単な形にする　→　まとめる
６－√１８/√２を有理化

（６－√１８）×√２/√２×√２＝（６√２－６）/２＝３√２－３
√２（１＋√３）（１－√３）を展開
√２（１＋√３）（１－√３）＝√２（１－３）＝－２√２

６－√１８/√２＋√２（１＋√３）（１－√３）＝３√２－３－２√２＝－３＋√２

問3：二次方程式

問3：（ｘ－１）²－７（ｘ－１）－８＝０を解く問題です。
【・答え　ｘ＝０,９】
ｘ－１をＸとおいて解いていく。
Ｘ²－７Ｘ－８＝０
（Ｘ－８）（Ｘ＋１）＝０
Ｘ＝８,Ｘ＝－１

求めたいのはｘなので、
８＝ｘ－１
ｘ＝９

－１＝ｘ－１
ｘ＝０

問4：変化の割合

問4：ｙ＝ａ/ｘ（ａは定数）のｘが３から５まで増加するときの変化の割合が１であるときのａの値を求める問題です。
【・答え　－１５】
変化の割合とは（ｙの増加量）/（ｘの増加量）で求められる。
まずｙの増加量を求める。（ｘ＝５を代入したｙの値）ー（ｘ＝３を代入したｙの値）は
ａ/５－ａ/３＝ー２ａ/１５
となる。ｘの増加量は５－３＝２であるから、変化の割合は
－２ａ/１５÷２＝１
となればよい。ａについて解くと、
ａ＝－１５

問5：確率

問5：２つの箱に入っているカードに書かれた数によって３つの袋から玉を移動させる操作をする問題について、ある事象の確率を求める問題です。
【・答え　４/９】
Ｐから２、Ｑから１が出ると（それぞれ最小の値が引かれると）、ａ＝６,ｃ＝７となり、ａ<ｃが常に成立することが分かる。そこで、ａ＜ｂ、ｂ＜ｃとなる組み合わせを見つければよい。
調べると、（Ｐ、Ｑ）＝（２,３）、（３,３）、（４,３）、（４,４）、（４,５）
の５通りが上記の条件を満たす。
組み合わせは全部で９通り（Ｐに３枚×Ｑに３枚＝９）なので、求める確率は
５/９
となる。

問6：統計

問6：初めに求めた平均の合計と、一部の標本を除いた時の平均の差異から、初めに求めた平均を求める問題です。
【・答え　１０．６℃】
ここ２年を除いた８年の最高気温の平均値＝初めに求めた１０年の最近気温の平均値（ｘ）＋0.3
となるので、左辺を導出する。
まず、１０年の平均値の合計は（平均）×（年数）＝ｘ×１０＝１０ｘ
ここから２年を除くので、
１０ｘ－２．６－１６．２
これが８年分の最高気温の平均値であるから８で割ると、
１０ｘ－１８．８/８

最初の式を元に立式して解くと、
１０ｘ－１８．８/８＝ｘ＋０．３
１０ｘ－１８．８＝８ｘ＋２．４
２ｘ＝２１．２
ｘ＝１０．６(℃)

問7：整数

問7：「２０２０－ｎの値が９３の倍数」「ｎ－７８０の値が素数」を同時に満たす自然数ｎを求める問題です。
【・答え　８１１】
「２０２０－ｎの値が９３の倍数」は
２０２０－ｎ＝９３ｍ（ｍは自然数）
で表すことが出来る。これをｎについて整理すると、
ｎ＝２０２０－９３ｍ　…ⅰ
と表せる。
次に「ｎ－７８０の値が素数」を満たせばいいので、ⅰを代入すると、
ｎー７８０＝２０２０－９３ｍ－７８０＝１２４０－９３ｍ＝３１（４０－３ｍ）
となる。これが素数であるためには、（４０－３ｍ）が１である必要がある。
４０－３ｍ＝１
ｍ＝１３
と一つに決まるので、これをⅰに代入する。
ｎ＝２０２０－９３×１３＝８１１

問8：二次関数

問8：二次関数について、ａとｂの値をそれぞれ求める問題です。
【・答え　ａ：１１/４８　ｂ：１/６】
Ａ，Ｂ，Ｃ，Ｄの座標を求める。
Ａの座標：
ｘ座標は４と分かっており、ｍの関数上にあるので、
ｙ＝ａ×１６＝１６ａ
したがって、Ａ（４,１６ａ）
とおける。

Ｂの座標：
ｘ座標はＣと同じであり、ｌの関数上にあるので、
ｙ＝－２ｂ＋
したがって、Ｂ（－２,－２ｂ＋４）

Ｄの座標：
ｘ座標はＡと同じであるから、ｘ＝４
Ｄはｎの関数上にあるので、
ｙ＝ｂ×４－３＝４ｂ－３
したがって、Ｄ（４,４ｂ－３）

Ｃの座標：
ｘ座標はＢと同じであり、ｙ座標はＤと同じである。
したがって、Ｃ（－２,４ｂ－３）
ＡとＢのｘ座標より、ＡＢの長さが６ｃｍであるから、
ＢＣの長さは
－２ｂ＋４－（４ｂ－３）＝－６ｂ＋７＝６
ｂ＝１/６
Ｂのｙ座標は
ー２×１/６＋４＝１１/３
となり、これはＡのｙ座標と同じなので、
１６ａ＝１１/３
ａ＝１１/４８

大問2：平面図形

問1：証明

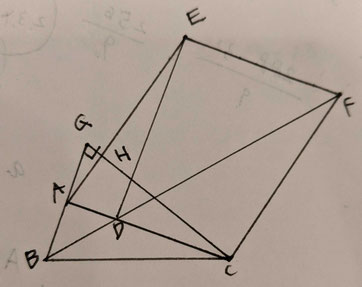
問1：四角形ＥＡＣＦが平行四辺形であることを証明する問題です。
【・証明例
問題文より、ＥＦ//ＡＣ　…①
△ＡＢＤはＡＢ＝ＡＤの二等辺三角形だから、∠ＡＢＤ＝∠ＡＤＢ　…②
ＡＢ//ＥＤであり、平行な２つの線の同位角は等しいから、∠ＥＤＦ＝∠ＡＢＤ　…③
①より、平行な２つの線の同位角は等しいから、∠ＥＦＤ＝∠ＡＤＢ　…④
②、③、④より、∠ＥＤＦ＝∠ＥＦＤであり、△ＥＤＦは二等辺三角形だから、ＥＦ＝ＥＤ　…⑤
△ＡＢＣ≡△ＤＡＥだから、ＣＡ＝ＥＤ　…⑥
⑤、⑥より、ＥＦ＝ＣＡ　…⑦
①、⑦より、一辺の対辺が平行かつ長さが等しいので、
四角形ＥＡＣＦは平行四辺形である。
】

問2 ①：辺の長さ

問2 ①：辺ＢＣの長さを求める問題です。
【・答え　４√３】
ＣＧの長さを求める　→　ＢＣの長さを求める

まずＣＧの長さを求める。ＡＣ＝６、ＡＧ＝２と分かっているので、ＣＧの長さは三平方の定理より、
ＣＧ²＋ＡＧ²＝ＡＣ²
ＣＧ²＝３６－４
ＣＧ＝４√２

次にＢＣの長さを求める。ＢＧの長さはＡＢ＋ＡＧ＝４よりＢＧ＝４とわかる。ＢＣの長さは三平方の定理より、
ＢＣ²＝ＢＧ²＋ＣＧ²
ＢＣ²＝１６＋３２＝４８
ＢＣ＝４√３

問2 ②：線分の長さ

問2 ②：線分ＥＨの長さを求める問題です。
【・答え　１４√３/５】
線分ＤＥと線分ＣＧの交点をＩとする。ＡＧ//ＥＤより、△ＡＧＨと△ＥＨＩが相似であることから、この相似比を求めることでＥＨを導出する。相似比を出すためにはＥＩの長さを導出する必要がある。

まず、△ＤＡＥ≡△ＡＢＣより、
ＡＥ＝ＢＣ＝４√３
ＣＤ＝ＣＡ－ＤＡ＝６－２＝４で求められる。
ＡＧ//ＤＩより△ＣＡＧ∽ＣＤＩとなるので、ＡＧ：ＡＣ＝ＤＩ：ＤＣの比が成り立つ。
これに代入してＤＩを求めると、
２：６＝ＤＩ：４
ＤＩ＝４/３
となる。ＥＩの長さはＥＤ－ＤＩで求められるので、
ＥＩ＝６－４/３＝１４/３

△ＡＧＨと△ＥＨＩの相似比はＡＧ：ＥＩ＝２：１４/３=６：１４＝３：７
であるから、ＥＨの長さは、
ＥＨ＝７/１０×ＡＥ＝７/１０×４√３＝１４√３/５ (ｃｍ)

問2 ③：面積

問2 ③：四角形ＥＨＣＦの面積を求める問題です。
【・答え　１０２√２/５】
△ＥＨＣ＋ＥＦＣの足し算として考える。
△ＤＥＡの面積の導出
①よりＣＧ＝４√２であるから、
△ＤＥＡ＝△ＡＢＣ＝ＡＢ×ＣＧ÷２＝２×４√２÷２＝４√２
△ＥＡＣの面積の導出
△ＤＥＡとＥＡＣの面積比はＡＤ：ＡＣで求められるから、
ＡＤ：ＡＣ＝２：６＝１：３
したがって、△ＥＡＣ＝３△ＤＥＡ＝１２√２
△ＥＦＣの面積の導出
△ＥＡＣと△ＥＦＣは平行四辺形ＥＡＣＦを対角線ＣＥで二分したものだから、面積は等しくなる。
したがって、△ＥＦＣ＝△ＥＡＣ＝１２√２
△ＥＨＣの面積の導出
△ＥＨＣとＥＡＣの面積比はＥＨ：ＥＡで求められるから、
ＥＨ：ＥＡ＝７：１０
したがって、△ＥＨＣ＝７/１０△ＥＡＣ＝４２√２/５

求める面積は、
△ＥＦＣ＋△ＥＨＣ＝１２√２＋４２√２/５＝６０√２＋４２√２/５＝１０２√２/５

大問3：立体図形

次の図について、各問題に答える大問です。

問1 ①：面積

問1 ①：△EJHの面積を求める問題です。
【・答え　６４/７(ｃｍ²)】

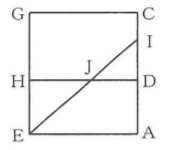
EJ+JIが最小となるとき、展開図上でJは線分EI上にあるので、△EJH＝1/2×HE×HJで求める。
GE//CAより、△EJH∽△IJDだから、HJ:DJ＝HE：DI＝4：3なので、HJ＝4/（4+3）HD＝4/7×8＝32/7（ｃｍ）
よって、△EJH＝1/2×4×32/7＝64/7（ｃｍ²）となる。

問1 ②：内角の大きさ

問1 ②：四角形ABIDの内角∠ＢＩＤの大きさを求める問題です。
【・答え　２ａ＋ｂ(°)】

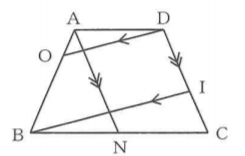
面ABCDについて、△EKH≡△AODなので、∠AOD＝∠EKH＝ｂ°である。
平行線の同位角は等しいので、OD//BIより、∠ABI＝∠AOD＝ｂ°である。
四角形ANCDは平行四辺形だから、AN=DC=5ｃｍである。
よって、△ABNはAB=ANの二等辺三角形だから、∠ANB＝∠ABN＝a+b（°）である。
平行線の同位角は等しいので、AN//DCより、∠DCN＝∠ANB＝a+b（°）である。
三角形の1つの外角は、これととなりあわない2つの内角の和に等しいから、
△BICについて、∠BID＝∠IBC+∠ICB＝a+（a+b）＝2a+b（°）である。

問1 ③：線分の長さ

問1 ③：線分KFの長さを求める問題です。
【・答え　１５/４(ｃｍ)】

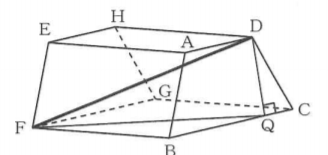
KF=OBなので、OBの長さを求める。
PD//BIより、PB：BC＝DI：IC＝3：（5-3）＝3：2なので、PB=3/2BC＝3/2×8＝12（ｃｍ）
AD//PCより、△AOD∽△BOPだから、OA：OB＝AD：BP＝4：12＝1：3
よって、OB＝3/（1+3）AB＝3/4×5＝15/4（ｃｍ）だから、KF=OB=15/4（ｃｍ）

問2 ①：線分の長さ

問2 ①：線分ＤＦの長さを求める問題です。
【・答え　１１(ｃｍ)】

上図のように、DからBCに対して垂線DQを引くと、DQは面FBCGに対して垂直なので∠DQF＝90°となる。
これより三平方の定理を利用して、DFの長さを求める。
四角形ABCDはAB=DCの台形なので、QC=（BC－AD）÷2＝（8－4）÷2＝2（ｃｍ）となる。
△CQDについて、DQ²＝DC²－QC²＝5²－2²＝21
BQ＝8－2＝6（ｃｍ）より、△BQFについて、FQ²＝FB²+BQ²＝8²＋6²＝100
△DFQについて、DF＝√（DQ²+FQ²）＝√21+100＝11（ｃｍ）

問2 ②：線分の長さ

問2 ②：線分ＡＭの長さを求める問題です。
【・答え　８√２１/１１(ｃｍ)】

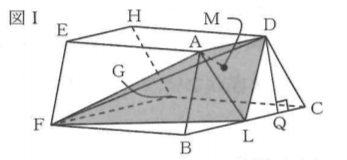
AMは上図Ⅰの色付きの三角錐ADFLにおいて、面DFLを底面としたときの高さなので、
三角錐ADFLの体積＝1/3×△DFL×AMから、AMの方程式を立てる。
三角錐ADFLは底面を△ADLとすると、高さはFB=8ｃｍとなる。
DQ=√21ｃｍとなるから、△ADL＝1/2×AD×DQ＝1/2×4×√21＝2√21（ｃｍ²）である。
三角錐ADFLの体積は、1/3×2√21×8＝16√21/3（ｃｍ³）である。
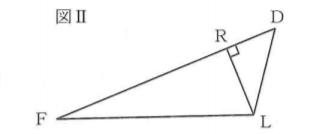
△DFLについて上図Ⅱのように作図し、DR=ｘｃｍとする。
三平方の定理を用いて、RL²を2通りのｘの式で表し、ｘの方程式を作る。
EF//DL，EF//ABより、AB//DLであり、AD//BLだから、四角形ABLDは平行四辺形なので、DL=AB=5ｃｍである。
△DRLについて、RL²＝DL²－DR²＝25－ｘ²・・・①
BL＝AD＝4ｃｍより、△LFBについて、FL²＝FB²+BL²＝8²+4²＝80であり、FR=DF－DR＝11－ｘ（ｃｍ）だから、
△FRLについて、RL²＝FL²－FR²＝80－（11－ｘ）²＝－ｘ²+22ｘ－41・・・②
①、②より、RL²について、25－ｘ²＝－ｘ²+22ｘ－41となり、ｘ=3を得る。
よって、RL＝√25－3²＝4ｃｍだから、△DFL＝1/2×DF×RL＝1/2×11×4＝22（ｃｍ²）である。
したがって、三角錐ADFLの体積について、16√21/3＝1/3×22×AMより、AM＝8√21/11（ｃｍ）

 大阪府のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、大阪府にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。