【滋賀県】平成31年度/2019年度入学者高校入試選抜試験：数学の解説
滋賀県の2019年3月実施の平成31年度（2019年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
滋賀県の数学は4つの大問から構成され、そのうち1つは必ず小問集合が出題されます。
難易度としては難です。癖のある問題が多く、しっかり理解をして解かないと大問の問題を全て間違えるということもあり得ます。
【滋賀県】平成31年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら＞＞
大問1：小問集合
問1：正負の数
問1：A市におけるある日の最高気温と最低気温の温度差は19℃だった。この日のA市の最高気温が15℃だったとき、最低気温は何℃だったか求める問題です。
【・答え「-4℃」】
15-19=-4 なので-4℃となる。
問2：文字と式
問2：1/4a-5/6a+a を計算する問題です。
【・答え「5/12a」】
与式=3/12a-10/12a+12/12a=5/12a
問3：連立方程式
問3：連立方程式x-2y=7，4x+3y=6 を計算する問題です。
【・答え「x=3，y=-2」】
x-2y=7 …①，4x+3y=6 …②とすると
①×3+②×2を解くと、x=3となる。…③
③を①に代入すると、3-2y=7 -2y=4 y=-2
問4：平方根
問4：√27+12/√3 を計算する問題です。
【・答え「7√3」】
与式=3√3+12√3/3=(9√3+12√3)/3=21√3/3=7√3
問5：二次方程式
問5：二次方程式2x²+4x-7=x²-2 を解く問題です。
【・答え「x=-5，1」】
与式をすべて左辺に移項すると、
x²+4x-5=0 (x+5)(x-1)=0 よって、x=-5，1
問6：多項式
問6：14x²y÷(-7y)²×28xy を計算する問題です。
【・答え「8x³」】
与式=(14x²y×28xy)/49y²=8x³
問7：二次関数
問7：関数y=-7x²のグラフ上にy座標が-28である点があり、その点のx座標を求める問題です。
【・答え「-2，2」】
-28=-7x² x²=4 x=±2
問8：確率
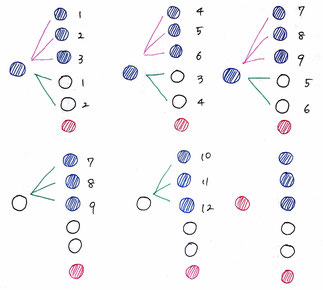
問8：青玉3個、白玉2個、赤玉1個が入った袋の中から玉を1個取り出して、それを袋に戻してかき混ぜてからまた1個取り出します。このとき、青玉が2回出る場合と、青玉と白玉が1個ずつ出る場合とではどちらが起こりやすいかについて考えた文中の空欄に当てはまる数と選択肢を選ぶ問題です。
【・答え「(a)…1/4 (b)…1/3 (c)…イ」】
6個の玉が入っている袋の中から1個取り出して、一度戻してからもう1個取り出すときに起こるのは6×6=36(通り)である。
青玉が2回出るのは画像の樹形図をピンク色で結んだ部分の9通りなので、9/36=1/4
青玉と白玉が1回ずつ出るのは画像の樹形図の緑色で結んだ部分の12通りなので、12/36=1/3
よって、イ「青玉と白玉が1回ずつ出る場合」の方が起こりやすい。
問9：平面図形
問9：AB=ACである二等辺三角形ABCについて①，②の問いに答える問題です。
①AB=9、BC=6のときにBE=3となる点Eをとり、辺BC上に∠BAC=∠BDEとなる点Dを取ったときの線分BDの長さを求める問題です。
②辺BCに平行な直線と、辺AB，ACの交点をF，Gとするとき、△AFGの面積が△ABCの面積の半分になるような点Fおよび点Gを、コンパスと定規を使って作図する問題です。
【・答え「①…9/2 ②…画像を参照」】
＊①
∠BAC=∠BDE、∠Bは共通から
2組の角がそれぞれ等しいので、△ABC∽△DBEであると言える。
相似な図形は辺の比がそれぞれ等しいので
AB：BC=DB：BE
AB=9、BC=6、BE=3、DB=BD
9：6=BD：3 6BD=27 BD=9/2
＊②
大問2：標本調査・資料の分析と活用
問1
問1：標本の選び方として最も適切なものを、選択肢ア～エの中から一つ選ぶ問題です。
【・答え「エ」】
ア…全校生徒が対象の調査なので、特定のクラスからだと偏りがあるため不適切。
イ…「協力してくれる人」=多くキャップを持ってきた人である可能性が高いので不適切。
ウ…アと同様、全校生徒が対象なので、特定の学年だけでは不適切。
エ…適切だと言える。
問2
問2：標本調査で30人選んで調査したときに、50個よりも多く持ってきた人は12人だったとすると、全校生徒では何人と推測できるか答える問題です。
【・答え194人】
全校生徒で50個より多く持ってきた人数をxとすると、
30：12=485：x 30x=5820 x=194
よって、194人。
問3
問3：3年生150人に全数調査を行った結果をまとめたヒストグラムを見ながら話している会話文中の下線部について、ヒストグラムから読み取ることができることをもとに「階級」「平均値」「度数」の3語を用いて説明する問題です。
【・答え「平均値が含まれる階級の度数より大きい度数の階級が、平均値より大きい値が含まれる階級と小さい値が含まれる階級に分かれている」】
平均値を含む階級の度数より度数の多い階級が、小さな階級と大きな階級の両方にあるということが説明できれば正解。
問4
問4：全クラス30人である3年生5クラスについて、各クラスの度数分布表を基に作成した5つのヒストグラムがそれぞれどのクラスのものかを《各クラスのヒストグラムから読み取れること》から考え、①，②の問いに答える問題です。
【・答え「①…60個以上80個未満 ②…58個」】
どのヒストグラムがどのクラスのものかを考えます。
「B，C，D組の中央値は、3クラスとも同じ階級にある」
→それぞれのヒストグラムからわかる中央値は
(Ⅰ)が60以上80未満の階級
(Ⅱ)が40以上60未満の階級
(Ⅲ)が60以上80未満の階級
(Ⅳ)が40以上60未満の階級
(Ⅴ)が40以上60未満の階級
なので、B，C，D組は(Ⅱ)，(Ⅳ)，(Ⅴ)のいずれかであることがわかる。
「B組は、C組より範囲が小さい」
→上記から、BとCは(Ⅱ)，(Ⅳ)，(Ⅴ)のどれかであるから
(Ⅱ)の範囲は120、(Ⅳ)の範囲は120、(Ⅴ)の範囲は80なのでB組のヒストグラムは(Ⅴ)だと言える。
「E組の中央値は、ヒストグラムからそれぞれ求めた最頻値や平均値と同じ階級に含まれている」
→それぞれのヒストグラムからわかる最頻値は
(Ⅰ)は80以上100未満の階級
(Ⅱ)は40以上60未満の階級
(Ⅲ)は60以上80未満の階級
(Ⅳ)は40以上60未満の階級
(Ⅴ)はB組なので省略
平均値は
(Ⅰ)は58で、40以上60未満の階級
(Ⅱ)は58で、40以上60未満の階級
(Ⅲ)は62で、60以上80未満の階級
(Ⅳ)は54で、40以上60未満の階級
(Ⅴ)はB組なので省略
このなかで中央値、最頻値、平均値が同じ階級にあるのは(Ⅱ)，(Ⅲ)，(Ⅳ)だが、
(Ⅱ)と(Ⅳ)はC組かD組なので、E組のヒストグラムは(Ⅲ)、A組は(Ⅰ)であると言える。
「A組とD組は、ヒストグラムから求めた平均値が同じ」
→上記から、平均値が同じなのは(Ⅰ)と(Ⅱ)なので、D組のヒストグラムは(Ⅱ)、よってB組は(Ⅴ)であると言える。
よって、①で(Ⅲ)のヒストグラムにおいて最頻値が含まれるのは60以上80未満の階級。
(Ⅱ)の平均値は58である。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3：文字と式、円
問1
問1：半径OAの長さを求める問題です。
【・答え「r=49.5」】
AD=9から、コップのフチの円周は9πであることがわかる。
コップ③は円を1周するのに11回転したことから、
円Oの円周は9π×11=99π であるから
直径は99、よって円Oの半径にあたるOA=99×1/2=49.5(cm)
問2
問2：コップ②を1回転させたときの∠AOSの大きさを求める。また、コップが円を1周するのに必要なコップの回転数が多くなったとき、∠AOSの大きさがどのように変化するか、選択肢ア～ウのなかから1つ選び、その理由を∠AOSの大きさをy°、コップの回転数をm回としてyとmの関係式を用いて説明する問題です。
【・答え「∠AOS=40° イ(説明は解説の通り)」】
コップ②は円を1周するのに9回転するので、
∠AOS=360°/9=40°
①、③の場合は、
①→1/7×360°≒51.4°
③→1/11×360°≒32.7°ｎ なので、回転数が多くなるほど∠AOSの大きさは小さくなる。
これらから考えて、∠AOS=y°、回転数=mとすると
y=360/m となるので、割る数である回転数(m)が大きくなればなるほどyは小さくなる。
問3
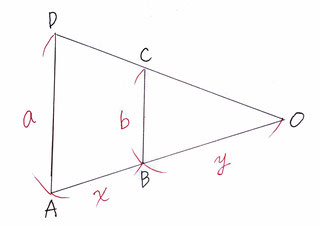
問3：線分ADの長さをa(cm)，線分BCの長さをb(cm)，線分ABの長さをx(cm)，コップの回転数をm(回転)として、a，b，x，mの文字を用いて説明し、その式になる理由をa，b，x，mの文字を用いて説明する問題です。
【・答え「m=2x/(a-b)」】
OB=yとして、図で表すと画像のようになる。
OA：OB=AD：BC (x+y)：y=a：b ay=b(x+y) ay=bx+by
ay-by=bx (a-b)y=bx y=b/(a-b)x …①
半径OBの円周の長さは
y=2π×y=2yπ
BCを直径とする円周の長さはbπだから
m=2yπ/bπ=2y/b …②
①に②を代入すると、
m=2/b×b/(a+b)x=2x/(a-b) となる。
大問4：平面図形
問1
問1：図1について、線分BEの長さをxを用いた式で表す問題です。
【・答え「BE=√2-x²」】
問2
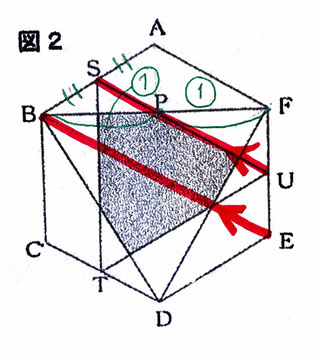
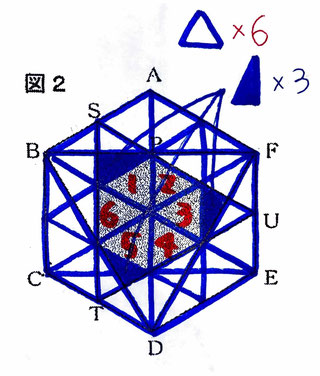
問2：図2について①～③の問いに答える問題です。
【・答え「①…解説の通り ②…4√15/3 ③…25√3/2」】
＊①
補助線BEを書き込むと、BE//SU
点SはABの中点なので、
AS：SB=1：1
よって、FP：PB=1：1
中点連結定理より、点Pは線分BEの中点である。
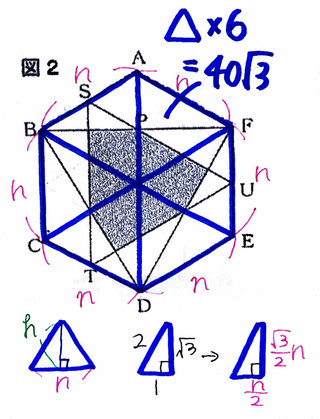
＊②
正六角形ABCDEFは正三角形が6つ集まった図形である。
正三角形を取り出すと、画像からもわかるように
正三角形を二等分すると辺の比が1：2：√3の直角三角形であることがわかる。
正六角形の1辺の長さをnとすると、正三角形は底辺がn、高さが√3/2nとなり、
正六角形の面積は40√3であるから、
(n×√3/2n×1/2)×6=40√3 が成り立ち、
これを解くと、6√3/4n²=40√3 n²=40√3×4/6√3=80/3
n=√80/√3=4√5/√3=4√15/3
＊③
斜線部分は、図で示した小さな正三角形が6つ分と、
その半分の直角三角形が3つ分であることがわかる。
正三角形は、②で6つの正三角形に分けたところから、さらに4つに分けた正三角形なので
1つ当たりの面積は、40√3×1/24=5√3/3 …①
直角三角形はその正三角形の半分の大きさなので、
5√3/3×1/2=5√3/6 …②
よって、(斜線部分の面積)=①×6+②×3 だから
5√3/3×6+5√3/6×3=10√3+5√3/2=25√3/2
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、滋賀県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
