







滋賀県の2020年3月実施の令和2年度(2020年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
滋賀県の数学は4つの大問から構成され、そのうち1つは必ず小問集合が出題されます。
難易度としては難です。癖のある問題が多く、しっかり理解をして解かないと大問の問題を全て間違えるということもあり得ます。
【滋賀県】令和2年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら>>
(1):A市における3月と4月の2カ月の人口の変化を求める問題です。
【・答え「-5」】
解説)3月の1ヶ月間と4月の1ヶ月間の人口の変化の和を考えればよいので、-11+6=-5である
(2):7a/4-3a/5を解く問題です。
【・答え「23a/20 」】
解説)与式=35/20 a-12/20 a=23/20 aしっかり通分して計算ミス無いように!
(3):2x-3y=1,3x+2y=8の連立方程式を解く問題です。
【・答え「x=2、y=-1」】
解説)2x-3y=1… ① 3x+2y=8… ②とする。①×2 + ②×3でyを消去すると
4x+9x=2+24 13x=26 x=2
②にx=2を代入すると、3×2+2y=8 2y=2 y=1
(4):√3(2-√6)を解く問題です。
【・答え「2√3-3√2」】
解説)与式=√3×2-√3×√6=2√3-3√2分配法則を使用し計算の順番を間違えないようにしよう!
(5):x²-7x+12=0を解く問題です。
【・答え「x=3,4」】
解説)積が12、和が-7となる2数を探すと、-3と-4が見つかるから、
(x-3)(x-4)=0より x=3,4
(6):x³×(6xy)²÷(-3x²y)を解く問題です。
【・答え「-12x³ y」】
解説)与式=x³×36x² y²÷(-3x² y)=(-x³×36x² y²)/(3x² y)=-12x³ y
文字の累乗の数を数え間違えないようにしよう!
(7):xの変域とyの変域から関数y=ax²を解く問題です。
【・答え「y=1/9x²」】
解説)0≦y≦1 より、y=ax²のグラフは上に開けた放物線なのでa>0であり、xの絶対値が
大きいほどyの値は大きくなる。よって、-3≦x≦1でのyの最大値は、x=-3の時のy=1
1=a×(-3)² 9a=1 a=1/9 これはa>0 を満たす。
(8):表を元に、最頻値を求める問題です。
【・答え「7」】
解説)最頻値とは、最も度数(人数)の多い値(小テストの点数)なので、7である。
(9):平行四辺形ABCDの中にAC//EFとなるE,Fをとり、C,D,E,Fと書かれたカードから2枚ずつ取り出し、Aとその他取り出したカードを結んで△DFCと同じ面積になる確率を求める問題です。
【・答え「1/2」】
解説)底辺の長さと高さの等しい三角形は
面積が等しいことを利用して解く。
AD//FCより、△DFC=△AFC
AC//EFより、△AFC=△AEC
AE//DCより、△AEC=△AED
なので
△DFC=△AFC=△AEC=△AED
である。
よって、4枚のカードのうち、CとF、CとE、DとEを引いた時に△DFCと同じ面積になる。
下の樹形図から2枚のカードの引き方は6通りあり、条件に合うのは樹形図の〇部分になる
為求める確率は3/6=1/2である。
旅行会社が企画した観光バスツアーの料金について調べた結果から(1)~(4)までの問いに答える問題です。
(1):参加者が15人のときの旅行会社の売り上げ金額を求める問題です。
【・答え「75000」】
解説)5000×15=75000 一人当たりの売り上げが5000円なので15人分計算するだけ!
(2):旅行会社の利益をプラスにするためには、少なくとも何人の参加者が必要になるのか求める問題です。
【・答え「26人」】
解説)観光バスツアーの参加者をx人とすると、旅行会社の利益は
5000x-(1900x+80000)=3100x-80000(円)
なので、3100xが8000より大きくなる最小の整数xを求めればいい。
3100x=80000のとき、x=80000÷3100=25.8
なのでxが26以上のとき、3100xが80000より大きくなる
よって、求める人数は26人である。
(3):調べたこと①~③の式をグラフに表したとき、x座標が40の点Aとx座標が0の点Bのy座標の差が表すものをア~オの中から選ぶ問題です。
【・答え「エ」】
解説)①②は比例であり、グラフは原点を通る直線となるので、2点ABを通っているグラフは、
③のグラフだとわかる。よってAのy座標はy=1900×40+80000
Bのy座標はy=1900×0+80000=80000なので、2点A.Bのy座標の差は1900×40+80000-80000=19×40である。
これは、参加者が40人の時のお弁当代、お土産代、美術館の入場料の合計(参加者1人につき1900円)を表しているので、求める記号はエである。
(4):45人の参加者がいたとき、旅行会社の利益を100000円以上にするために1人あたりの参加費を少なくともいくらにする必要があるか求める問題です。
【・答え「5900円」】
【説明】一人あたりの参加費をA円とすると、旅行会社の売上金額の合計は、45×A(円)となる。
また、旅行会社が観光バスツアーを開催するための費用の合計は、1900×45+80000=165500
となり、100000円の利益を出すためには、100000=45A-165500 45A=165500+100000
45A=265500 A=5900
したがって、一人当たりの参加費を5900円以上にすると、100000円以上の利益を出すことができる。
【一人当たりの参加費】 5900円
解説)表やグラフを見ながら解く問題はややこしく感じるが、一つ一つ読み解けば必ず解けるようになっているのであきらめずに頑張ろう!
展示室にあるパネルによって見えなくなる壁面があることを説明するために行った考えをもとに、(1)~(3)の問いに答える問題です。
(1):点Pが点Aにあるときの線分CGの長さと、点Gが点Dに重なったときの線分APの長さを求める問題です。
【・答え「線分CG:2 線分AP:6」】
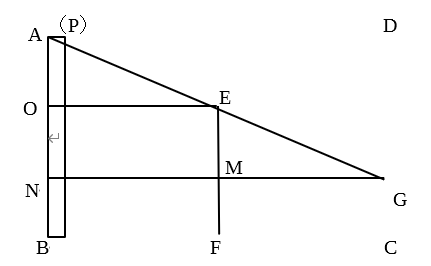
上の図のように作図する。OE//NGより、
△AOE∽△ANGであり、相似比は、
OE:NG=BF:BC=6:12=1:2である。
AO=AB-EF=8-5=3(m)なので
AN=2AO=6(m)である。よって、OG=DC-DG=AB-AN=8-6=2(m)である。
四角形ANGDは長方形なので、対角線の交点はそれぞれの対角線の中点であるEを通ることが分かる。したがってGがDに重なるとき、半直線DEと辺ABとの交点はNとなるから。AP=AN=6(m)となる。
(2):点Pが線分BF上を点Bから2m移動した時、半直線FEと辺ADの交点をHとしたとき、△PFEと△GHEが相似であることを証明し、線分DGの長さを求める問題です。
【・答え「証明は以下参照、線分DG・・・18/5」】
【証明】
△PFEと△GHEについて、対頂角は等しいので∠FEP=∠HEG・・・①
辺ADと辺BCは並行であるから、平行線の錯角は等しいので、∠EPF=∠EGH・・・②
①、②から、2組の角がそれぞれ等しいので△PFE∽△GHEといえる。
解説)相似の証明は、対頂角や平行線の錯角の性質から、解答例になる。
△PFE∽△GHE、PF=6-2=4(m)より、PF:GH=FE:HE 4:GH=5:(8-5)
GH=(4×3)/5=12/5(m) DG=6-12/5=18/5(m)である。
(3):点Pが辺CD上を点Cから点Dまで移動する。線分CPの長さが線分AGの長さと等しくなるとき、線分CPの長さを求めなさい。
【・答え「(11-√73)/2」】
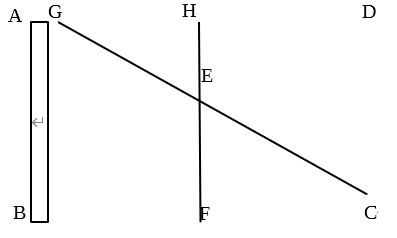
解説)上の図のように作図する。HE//DPより、
△GHE∽△GDPである。
CP=AG=xmとすると、GH=6-x(m)
GD=12-x(m)、HE=8-5=3(m)
DP=8-x(m)、GH:GD=HE:DPなので
(6-x):(12-x)=3:(8-x)となる。
計算していくと、
(6-x)(8-x)=3(12-x) 48-14x+x²=36-3x
x²-11x+12=0 となる。
2次方程式の解の公式を使用し、
x=(-(-11)±√(〖(-11)〗^2-4×1×12))/(2×1)=(11±√73)/2
0≦x≦8であり、√64<√73<√81より8<√73<9である。
したがってx=(11+√73)/2は、(11+8)/2=9.5より大きいので 0≦x≦8を満たさない。
x=(11-√73)/2は、(11-9)/2=1 より大きく (11-8)/2=1.5より小さいので0≦x≦8
を満たす。したがって、CPの長さは、 (11-√73)/2mである。
大問3と同じ平面図形が単元としては題材ですが、独特な内容になっています。
円の面積を三等分する方法を参考にして(1)~(3)までの問いに答える問題です。
(1):円の面積を三等分する方法が可能なことを証明する問題です。
【・答え「以下参照」】
【証明】
点Aから半径OAと長さが等しい点B、また点Bからも、半径OAと長さが等しい点Dを取るので、△AOB、△BODは正三角形である。
したがって、∠AOB=60°・・① ∠BOD=60°・・②
①+②より、∠AOD=120°・・③ 同様にして、∠AOE=120°・・④
③、④より∠DOE=360°-240°=120°・・⑤
③、④、⑤により、3つの扇形の中心角は、それぞれ120°になるので、3つの扇形の面積は、それぞれ円の面積の120/360倍になり、等しくなる。
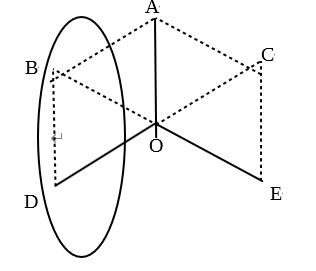
解説)上の図のように円1周が360°であることを利用し、
∠AOD=∠AOE=∠DOE=360÷3=120°となれば円が三等分されていることが分かる。
よって正三角形の性質を利用すれば解答例のように答えることができる。
(2):正方形ABCDの対角線の交点Pを通る線分を使い、面積を三等分し、EB=GC,∠PFD=90°となるように点E,F,Gを取ったとき、線分EP,FP,GPで切り分けたときに正方形ABCDの面積が三等分になるような線分AEと線分EBの長さの比を求める問題です。
【・答え「5:1」】
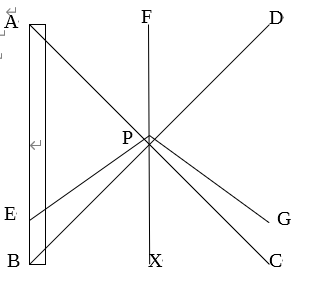
解説)上の図のように作図し、FP=PX=AF=a EB=b とする。
台形AEPFと台形PEBXの面積比は2:1であり、二つの台形の高さがAF=aなので、
(上底)+(下底)の長さの比は2:1である。AE=AB-EB=2a-bより
(a+2a-b):(a+b)=2:1
3a-b=2(a+b) 3a-b=2a+2b a=3b
よって、AE=2×3b-b=5bなので
AE:EB=5b:b=5:1である
(3):辺の長さが異なる三角形ABCの面積が三等分になるような点Q,E,Fと線分BQ,EQ,FQを作図する問題です。
【・答え「下図参照」】
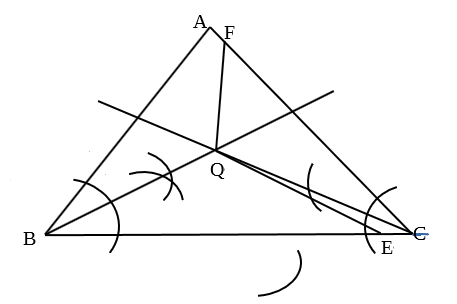
解説)2つの辺から等しい距離にある点は2つの辺で出来た角の2等分線上にあるので、Qは∠ABCの2等分線と∠ACBの2等分線の交点である。
この時、Qから3辺AB、BC、CAまでの距離は等しいので、この長さを2sとする。
Qから3辺AB、BC、CAに引いた垂線が2Sになる。
△ABC=△QAB+△QBC+△QCA=1/2×AB×2s+1/2×BC×2s+1/2×CA×2s
=1/2(AB+BC+CA)×2s=(6+8+7)×s=21s
よって、△ABCの面積が三等分になるとき、1つの図形の面積は21s÷3=7sとなる。
△QBE=7sなので、1/2×BE×2s=7Sより。BE=7
したがって、ACの長さにンパスを合わせ、BC上にEを取る。
EC=8-7=1より、△QEC=1/2×1×2s=s△QCF=7s-s=6sなので、
1/2×CF×2s=6sよりCF=6なるFをとる(ABの長さを取る)。
家庭教師のやる気アシストは、滋賀県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3%という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから!
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

