【滋賀県】令和3年度/2021年度入学者高校入試選抜試験：数学の解説
滋賀県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
今年の滋賀県の数学は4つの大問から構成され、小問集合・図形が2つ・関数という構成でした。
難易度としては激難です。全国の中でも有数の難易度になっているかと思います。
唯一の救いは小問集合です。ここが簡単なので確実に得点を取っておきたいです。またその他の大問の（1）は必ず解けるようにしておくと良いと思います。
【滋賀県】令和3年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら＞＞
大問1：小問集合、難易度：易
次の（1）から（9）までの各問いに答えなさい。
（1）２×（－３）＋１を計算しなさい。
【答え】－５
【解説】2×(-3)+1=-6+1=-5
（2）5a/3－3a/4を計算しなさい。
【答え】(11/12)a
【解説】5a/3-3a/4=20a/12-9a/12=11a/12
（3）次の連立方程式を解きなさい。
ｘ－3ｙ＝6
2ｘ＋ｙ＝5
【答え】x=3,y=-1
【解説】x-3y=6を①,2x+y=5を②として②-2*①よりy=-1,①に代入してx=3
（4）6/√2＋√8を計算しなさい。
【答え】5√2
【解説】6/√2=6/√2×√2/√2=3√2,√8=2√2より3√2＋2√2が答えとなる。
（5）次の2次方程式を解きなさい。
ｘ²＋ｘ＝6
【答え】x=2,-3
【解説】x²+x-6=0→(x+3)(x-2)=0
（6）15a³b²÷5ab²/2を計算しなさい。
【答え】6a²
【解説】15a³b²×2/5ab²=6a²
（7）下の表は、関数y=ax²について、ｘとｙの関係を表したものです。このとき、aの値および表のbの値を求めなさい。
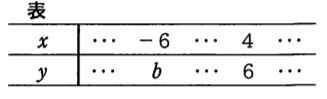
【答え】a=3/8,b=27/2
【解説】x=4,y=6をy=ax²に代入。a=3/8が決定。x=-6をy=3/8x²に代入。b=27/2
（8）大小2個のさいころを同時に投げたとき、大きいさいころの出た目を十の位の数、小さいさいころの出た目を一の位の数として2けたの整数をつくる。このとき、2けたの整数が素数となる確率を求めなさい。ただし、さいころは、1から6までのどの目が出ることも同様に確からしいとします。
【答え】2/9
【解説】条件を満たすような出目は(大、小)=(1,1)(1,3)(2,3)(3,1)(4,1)(4,3)(5,3)(6,1)の8通り。2つのサイコロを同時に投げた時の出目の総数は36通りであるから、8/36=2/9
（9）下の度数分布表は、ある学級の生徒の自宅から学校までの通学時間を整理したものです。この表から通学時間の平均値を求めると20分であった。（ア）、（イ）にあてはまる数と最頻値を求めなさい。
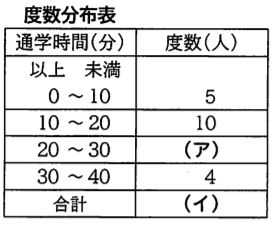
【答え】（ア）13、（イ）32、最頻値25
【解説】階級20~30の人数をxとする。度数分布表において平均値を求める場合、(階級値×度数の和/人数の和)で求められるから、次式が成り立つ。
(5×5+15×10+25×x+35×4)/(5+10+x+4)=20 よってx=13
これにより(ア)=13,(イ)=32が決定する。
また最頻値は度数が13である20~30の階級の階級値をとれば良い。
大問2：図形、難易度：難
太郎さんは、花子さんと体育大会で使う応援用のメガホンを学級の人数分作ることにしました。後の（1）から（4）までの各問いに答えなさい。
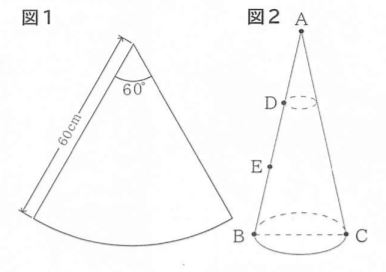
まず、ボール紙に図1の展開図をかき、母線の長さが60ｃｍの円すいの形を作ると図2のようになりました。点Ａは頂点、線分ＢＣは底面の直径を表しています。また点Ｄ，Ｅは、母線ＡＢを3等分する点です。
（1）図2の直径BCの長さを求めなさい。
【答え】20πｃｍ
【解答】図1の扇形の弧の長さは60×2×π×60/360=20π
次に、点Dを通り、底面に平行な平面でこの円すいを切って図3のメガホンを作りました。線分DFはメガホンの上面の円の直径を表しています。図4の実線は、図3のメガホンの展開図です。このメガホンに図5のような飾りのついたひもを側面に巻き付けながら貼り付けて完成となります。
2人は飾りのついたひもをどのように巻き付けるか、またどれくらいの長さのひもが必要かを考えました。ただし、ボール紙の厚さとひもの太さは考えないものとします。
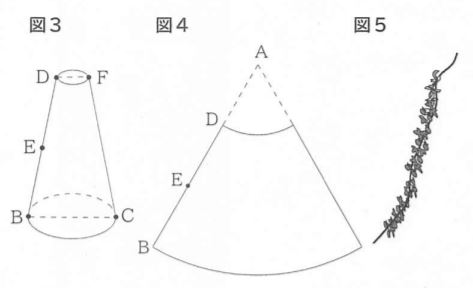
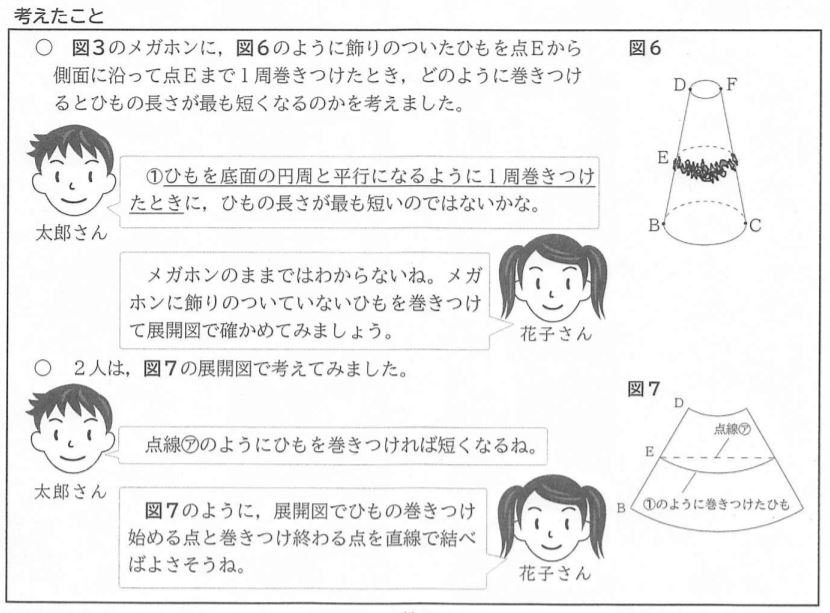
（2）下線部①のように太郎さんがひもを巻き付けたとき、ひもと線分FCとの交点Pをコンパスと定規を使って作図しなさい。ただし、作図に使った線は消さないこと。
【解説】Dとその右側にある点をD’とし、それぞれの点からコンパスで同じ半径で弧を描き、2点から等しい距離にある点を作図する。
その点と点Aを通るような直線を引き、点D、点Bが含まれる弧との交点がそれぞれ点F、点Cである。直線FCとその垂直二等分線の交点が点Pである。
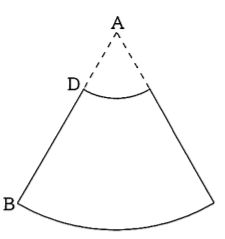
（3）次に太郎さんは、図8のようにひもを点Eから側面に沿って線分FCを横切って点Dまで巻き付けようと考えました。巻き付けるひもの長さが最も短いときのひもの長さを求めなさい。
【答え】20√3cm
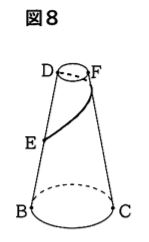
【解説】母線AIを3等分する点をG,Hとすると、AE=AH.
∠A=60°であるから△AEHは正三角形.
本問では図1中の線分DHの長さを問われているので、△DHEについて各辺の比が1:2:√3であることを用いれば求めることが可能である
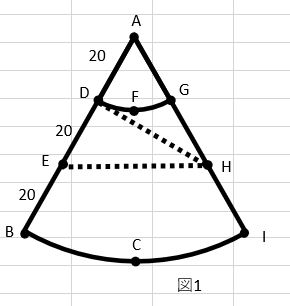
（4）さらに太郎さんは、ひもを点Bから側面に沿って線分FCを2回横切って点Eまで巻き付けようと考えました。図9は、花子さんと考えたことを応用して、ひもの長さが最も短くなるように巻き付ける様子を表したものです。巻き付けるひもの長さを求めなさい。
【答え】20√19cm
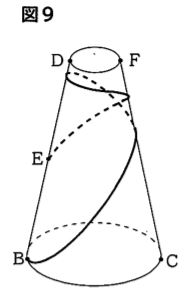
【解説】本問で問われている長さは図2中の線分BH(点線部分)である。
△ABJは辺の比が1:2:√3の直角三角形であるから、BJ=30√3
△BJHについて三平方の定理を用いることでBHの長さが求められる。
JH=JA+AH=30+40=70であるから
BH²=BJ²+JH²=2700+4900=7600
BH=20√19
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3：図形、難易度：難
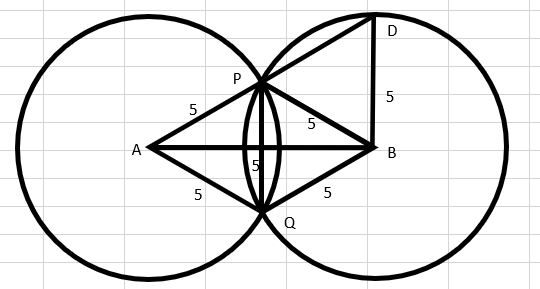
太郎さんと花子さんは、数学の授業で円について学習した後、2点で交わる2つの円について調べることにしました。太郎さんは、次の手順でノートに右の図をかきました。後の（1）から（3）までの各問いに答えなさい。
①から③の手順で、線分ABの長さや円の半径をいろいろ変えて調べます。
（1）太郎さんは、まず線分ABの長さを8ｃｍにして、円の半径をいろいろ変えて調べました。すると、4点Ａ，Ｂ，Ｐ，Ｑが、点Ｃを中心とする円周上にある場合がありました。このとき、線分ＡＰの長さと∠ＡＰＢの大きさを求めなさい。
【答え】AP：4√2cm、∠ＡＰＢ：90°
【解説】点Cを中心とする円上にA,B,P,QがあることからAC=CP=CB=4cm
△ACPは∠ACP=90°,AC=CPの直角二等辺三角形であるから、辺の比が1:1:√2であることを用いてAP=4√2
△ACPと△BCPはともに直角二等辺三角形であり∠APBはそれらの底角の和で表されるので∠APB=45°+45°=90°
太郎さんと花子さんは、図を見て気付いたことを話しています。
（2）2人の会話の中にある太郎さんの言った波線部の考え方を使って、下線部を証明しなさい。
【答え】
△APQと△BPQについて、
仮定より、AP＝BP･･･①、AQ＝BQ･･･②、PQは共通･･･③
①～③より、3組の辺がそれぞれ等しいから、△APQ≡△BPQである。
合同な三角形の対応する角の大きさは等しいので、∠APQ＝∠BPQ･･･④
よって、PQは∠APBの二等分線である。
次に、△APCと△BPCについて、PCは共通…⑤
④より、∠APC＝∠BPC…⑥
①、⑤、⑥より、2組の辺とその間の角がそれぞれ等しいから、△APC≡△BPC
よって、合同な三角形の対応する角の大きさはそれぞれ等しいので、∠ACP＝∠BCP
よって、∠ACP＋∠BCP＝2∠ACP＝180°
∠ACP＝90°より、AB⊥PQ
（3）AP＝PQ=5ｃｍのとき、線分ＡＰの延長線が点Ｂを中心とする円と、点Ｐ以外にもう1点で交わりました。その交点をＤとしたとき、線分ＰＤの長さを求めなさい。
【答え】5cm
【解説】問題の条件よりAP=PQ=5cm.
2つの円は半径が等しいのでAP=AQ=BP=BQ=5cm.
同じ円の半径であるからBP=BD=5cm.
以上より△APQと△BPQは正三角形であるから∠BPD=180°-(∠APQ+∠BPQ)=60°
△BPDは底角が60°の二等辺三角形、すなわち正三角形であるのでPD=5cm
大問4：関数、難易度：難
太郎さんは、寒かったので衣類に貼るカイロを貼ろうとしました。裏紙（剥離紙）をはがすとき、カイロの粘着部分の形や面積が変化していくことに気付き、下のような考え方をもとに、その変化について考えました。後の（1）から（4）までの各問いに答えなさい。
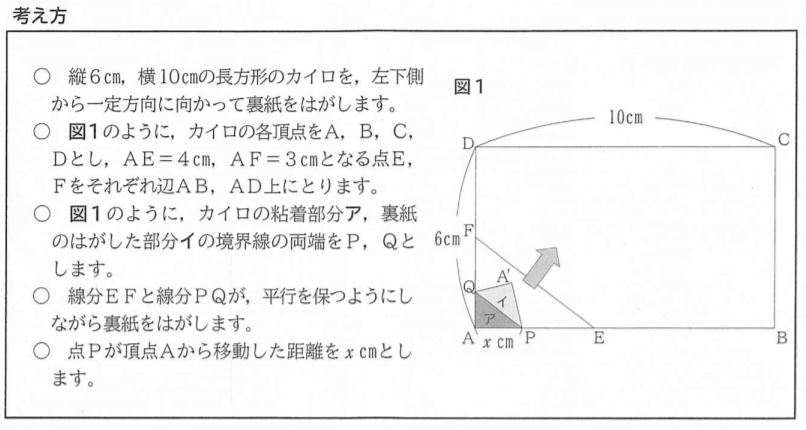
（1）裏紙をはがし始めてから、はがし終えるまでのｘの変域を表しなさい。
【答え】0≦x≦16
【解説】剥がし終えるまでの点Pの動きはA→B→Cであるからxがとりうる値は0から10+6=16までである。
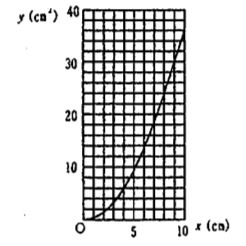
（2）0≦ｘ≦10のとき、カイロの粘着部分アの面積をｙｃｍ²とする。ｘとｙの関係をグラフに表しなさい。
【解説】PQ//EFを用いて△APQ∽△AEF
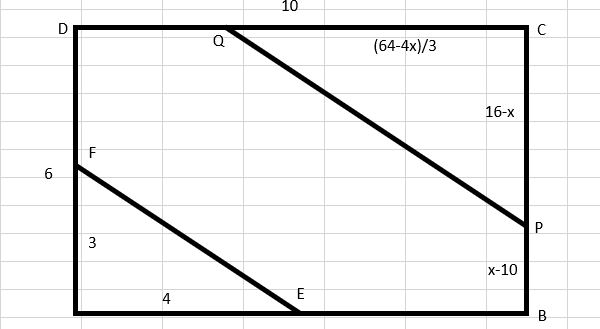
（3）裏紙をはがしていくと、カイロの粘着部分アの面積が、長方形ABCDの面積の5/8になりました。このときのｘの値を求めなさい。
【答え】x=16-3/2 √15
【解説】(長方形ABCDの面積の5/8)=10×6×5/8=75/2
x≦8の時、yの最大値はy=8×6/2=48<75/2
x≦10の時、yの最大値はy=6×10-24=36<75/2
すなわち面積が75/2になるのは点Pが辺BC上に存在する時である。
点Pが辺BC上に存在する場合について以下考察する。AB+BP=xであるから、BP=x-10(∵AB=10)
BP+PC=6であるからPC=6-(x-10)=16-x
PQ//EFから△AFE∽△CQP(詳細な証明は割愛)であるから、AF:AE=CP:CQ
3:4=16-x:CQ
CQ=(64-4x)/3
この時△CQP=6×10-75/2=45/2であるから、(16-x)×(64-4x)/3×1/2=45/2が成立。
(16-x)×(64-4x)=135
4×(16-x)²=135
16-x=±√135/2=±3√15/2
x=16±3√15/2
ここでxについての範囲が0≦x≦16であることからx=16+3√15/2は不適。
以上よりx=16-3√15/2
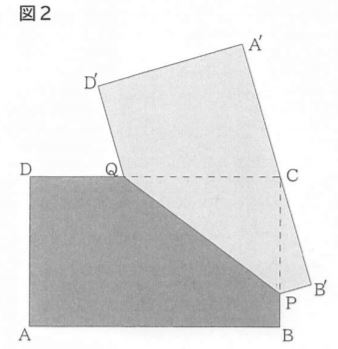
（4）図2のように、辺A’B’上に頂点Cが重なるまで裏紙をはがしました。このときｘの値を求めなさい。
【答え】x=181/16
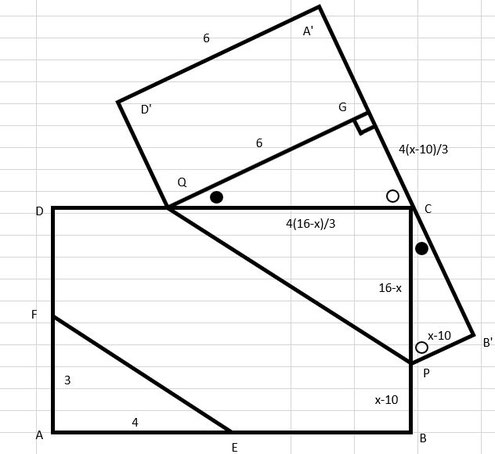
【解説】A’D’//QGになるような点GをA’B’上にとる。
前問と同様、AB+BP=xからPC=16-x,CQ=4(16-x)/3である。(詳細は前問参照)
三角形の内角の和が180°であることと直線が180°であることを利用すれば△GQC∽B’CPである。(詳細な証明は割愛)
よってB’P:PC=GC:CQであるから、
(x-10):(16-x)=GC:4(16-x)/3
GC=4(x-10)/3
△GQCについて三平方の定理を用いて
{4(16-x)/3}²={4(x-10)/3}²+6²
16×(16-x)²=16×(x-10)²+324
(16-x)²=(x-10)²+81/4
(16-x)²-(x-10)²=81/4
{(16-x)+(x-10)}{(16-x)-(x-10)}=81/4
6(26-2x)=81/4
26-2x=81/24=27/8
208-16x=27
16x=181
x=181/16
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、滋賀県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
