【滋賀県】令和4年度/2022年度入学者高校入試選抜試験：数学の解説
滋賀県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
【滋賀県】令和4年度一般入学者選抜の過去問はこちらから
数学の過去問題はこちら＞＞
大問1
問題文
次の（1）から（9）までの各問いに答えなさい。
（1）12－6÷（-3）を計算しなさい。
（2）1/2a－4/3aを計算しなさい。
（3）A＝4ｘ-1、B＝-2ｘ+3とするとき、次の式を計算しなさい。
-4A+3B+2A
（4）-15a²b÷3ab²×（-2b）²を計算しなさい。
（5）（√2－√3）²+√6を計算しなさい。
（6）次の2次方程式を解きなさい。
ｘ²＝ｘ+12
（7）関数ｙ＝-3ｘ²について、ｘが-4から3まで増加したときの、ｙの変域を求めなさい。
（8）3，4，5，6，7の数字の書かれたカードが1枚ずつある。この5枚のカードから同時に2枚のカードを引くとき、2枚のカードの数字の積が2の倍数でなく、3の倍数でもない確率を求めなさい。ただし、どのカードを引くことも同様に確からしいとします。
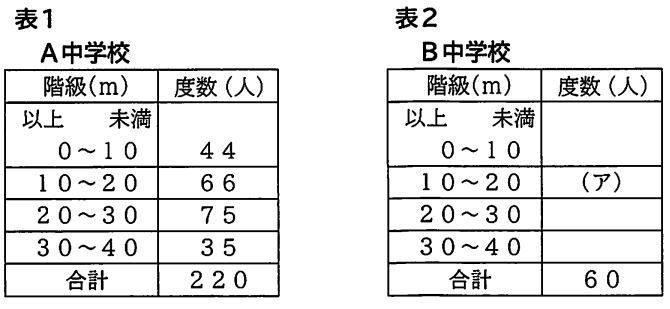
（9）下の表1は、A中学校におけるハンドボール投げの記録を度数分布表に整理したものです。表1をもとに、表2のB中学校の度数分布を推定します。A中学校とB中学校の10ｍ以上20ｍ未満の階級の相対度数が等しいとしたとき、表2の（ア）にあてはまる度数を求めなさい。
解答・解説
（1） 【正答 14】
加減乗除は乗除から計算する
【与式】＝12+2＝14
（2） 【正答 −5a/6】
展開して計算すればよい
【与式】＝（3a-8a）/6＝−5a/6
（3） 【正答 -14ｘ+11】
【与式】＝-2Ａ+3Ｂ
Ａ、Ｂをそれぞれ代入して、
-2Ａ+3Ｂ＝-2（4ｘ-1）+3（-2ｘ+3）
＝-8ｘ+2-6ｘ+9
＝-14ｘ+11
（4） 【正答 -20ab】
（5） 【正答 5-√6】
【与式】＝2-2√6+3+√6
（6） 【正答 ｘ＝-3、-4】
【与式】＝x²-x-12＝0
⇔(x-4)(x+3)＝0
⇔ｘ＝-3、-4
（7） 【正答 -48≦y≦0】
ｙ＝-3ｘ²にｘ＝0を代入してｙ＝0
ｙ＝-3ｘ²にｘ＝-4を代入してｙ＝-48
（8） 【正答 1/10】
条件を満たす数字の組み合わせは、5、7の1通りのみ。
数字の組み合わせ方は10通りあるので、求める確率は1/10。
大問2
問題文
優さんは、コンピュータを使って、関数のグラフや図形について調べました。このコンピュータでは、一次関数ｙ＝ax+bのaとbに値を代入すると画面に直線が表示されます。後の（1）から（4）までの各問いに答えなさい。
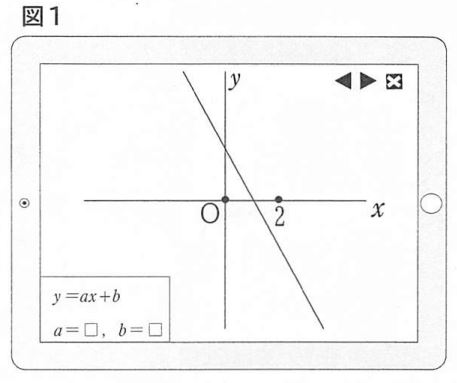
はじめに、優さんは、aとbにある値を代入すると図1の直線が表示されました。
（1）優さんが代入したaの値は、正の値、負の値、0のいずれになりますか。また、3a+bの値は、正の値、負の値、0のいずれになりますか。それぞれ答えなさい。
さらに、優さんは、aとbの値をいろいろと変えました。
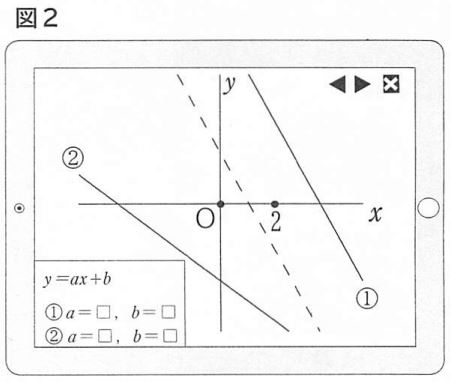
（2）図2の②の直線を表示するには、図1の直線とくらべて、aとbの値をどのように変えましたか。下線部のように「aの値は～bの値は～」の形式で答えなさい。
次に優さんは、コンピュータの画面上に4点A,B,C,Dをとり、四角形ABCDを表示しました。そして、図3のように、点B,C,Dは動かさず、点Aは点線上を動かすことにしました。
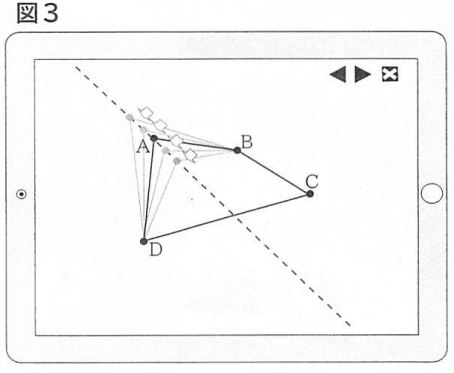
図4は、点Aが①、②、③、④の順に点線上を動くとき、点AとB、BとC、CとD、DとAを線分で結んでできる図形が変化していく様子を表しています。
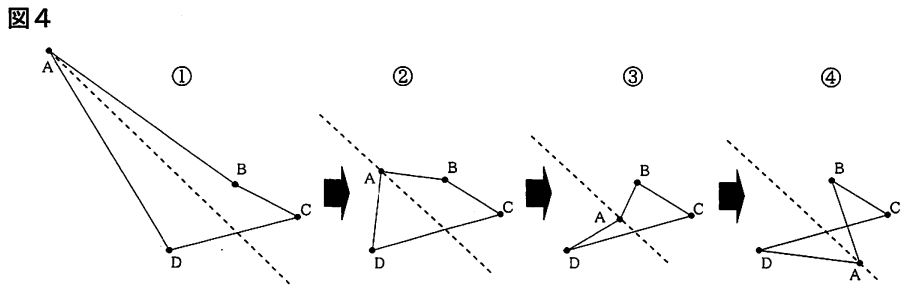
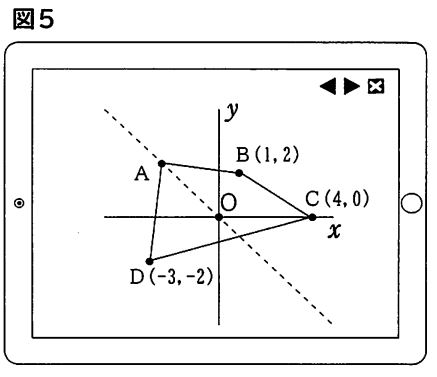
優さんは、この変化の様子を図5のように座標平面上で考えました。3点の座標を、B（1,2）C（4,0）D（-3,-2）とし、点Aは点線で示された直線ｙ＝-ｘ上を動くこととします。
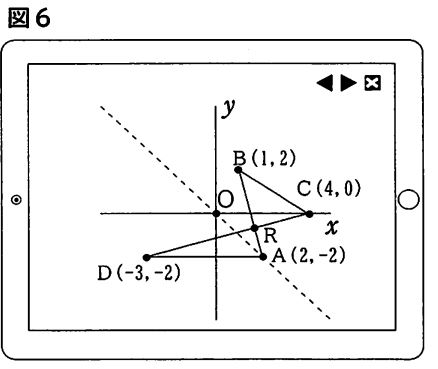
（4）図4の④のような2つの三角形が出来る場合、点Aの座標が（2，-2）のときに2つの三角形の面積が等しくなりました。図6のように、線分ABと線分CDの交点をRとすると、△RADと△RBCの面積が等しくなることを証明しなさい。
解答・解説
（1） 【正答 (aの値)負の値 (bの値)負の値】
グラフの傾きからaの値は負。
y＝ax+bにx＝3を代入したときのグラフの値を読み取ると、負の値になっている。
（2） 【正答 aの値は大きくする bの値は小さくする】
図1の直線とくらべて、傾きが緩くなっているので、aの値は大きくする。
図1の直線とくらべて、切片の値は小さくなっているので、bの値は小さくする。
（3） 【正答 S：T＝1：4】
線分BDと直線y＝-x、直線BCと直線y＝-xのそれぞれの交点をA´、A´´とする。
S＝△BCD、T＝△A´´CDとおける。
直線BCは、傾きが(2-0)/(1-4)＝-2/3なので、
y＝-2/3x+bに(4,0)を代入して、
y＝-2/3x+8/3 ー①
y＝-xと①より、点A´´(-8,8)
BC＝√{(4-1)²+(0-2)²}＝√13、
A´´C＝√{(-8-4)²+(8-0)²}＝4√13、
△BCD、△A´´CDにおいて、線分BC、A´´Cを底辺とすると高さな同じである。
よって、底辺の長さの比が、面積の比と等しくなるので、
S：T＝△BCD：△A´´CD＝√13：4√13＝1：4
（4） 【正答 (例)
直線ACの傾きは１、直線DBの傾きも１
よってAC//DB ー①
△ADCと△ABCについて、ACを底辺とする①より△ADC＝△ABC ー②
△RAD＝△ADC－△ARC、△RBC＝△ABC－△ARC
②より△RAD＝△RBCの距離は等しい 】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問3
問題文
涼さんと純さんは、食パンとロールパンをつくります。次の（1）から（3）までの各問いに答えなさい。
（1）涼さんは、つくったロールパンを友人に同じ個数ずつ配りたいと考えています。4個ずつ配ると9個あまり、6個ずつ配ると5個足りません。友人の人数を求めなさい。
食パン1斤とロールパン6個をつくるために使う小麦粉とバターの分量は、次のとおりです。
（2）純さんは食パンとロールパンをつくるために、小麦粉1.5ｋｇ、バター80ｇを用意しました。用意した小麦粉とバターは残さずに使います。純さんは、食パンとロールパンをそれぞれいくつつくる予定ですか。方程式をつくり、答えを求めなさい。ただし、答えを求めるまでの過程も書きなさい。
2人は、図1のような食パン1斤を焼き上げたあと、食パンを2つ切って2人で分けました。図2は純さんの食パンを表し、図3は、図2の食パンの大きさを表しています。ただし、食パン1斤を直方体とみて、頂点E,F,G,Hが同じ平面上にあるとします。
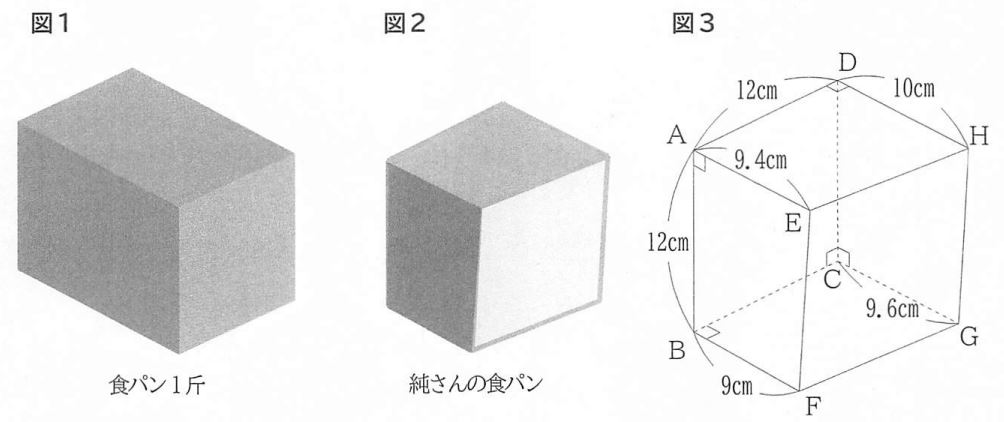
（3）純さんは図3の四角形EFGHが平行四辺形であることに気づきました。このときの、対角線FHの長さを求めなさい。
解答・解説
（1） 【正答 7人】
友人の人数をx人とすると、ロールパンの個数はそれぞれ、
4x+9(個)ー①、6x-5(個)ー②
①、②より
4x+9＝6x-5
⇔x＝7
（2） 【正答 (食パン)2斤 (ロールパン)36個
(求める過程)食パンをx斤、ロールパンをy個つくるとすると、
小麦粉が1.5㎏だから、300x+150y/6＝1500 ー①
バターが80gだから10x+10y/6＝80 ー②
①より12x+y＝60 ー③
②より6x+y＝48 ー④
③－④より6x＝12 x＝2
④よりy＝36 】
（3） 【正答 17㎝】
線分FHを対角線とする直方体をつくる
点Hと点Fは10-9＝1㎝分座標に差があり、直方体の高さと横の長さは12㎝なので、
直方体の対角線を求める公式√(a²+b²+c²)に代入して
√(12²+12²+1²)＝√289＝17
大問4
涼さんと純さんは、体育の授業中に3人で行うダンスの隊形移動について考えています。3人の位置を点A,B,Cとします。後の（1）から（4）までの各問いに答えなさい。
はじめに、点A,B,Cを図1の①から②、②から③の順に動かすことにしました。ただし、①において、点A,B,Cは一直線上にあり、AB＝AC＝2ｍとします。
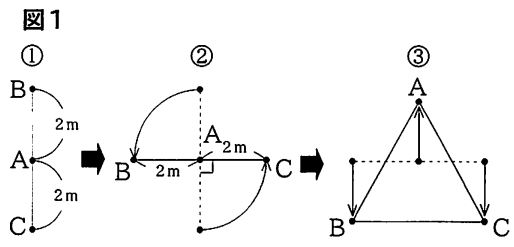
（1）図1の②のように、点B、Cは点Aを中心とする半径2ｍの円周上を反時計回りに90°それぞれ動きます。点Ｂ，Ｃがそれぞれ動くとき、点Ｂ，Ｃの2点が動く距離の合計を求めなさい。
次に、2人は、図1の③から点Ａ，Ｂ，Ｃを動かすことを考えています。
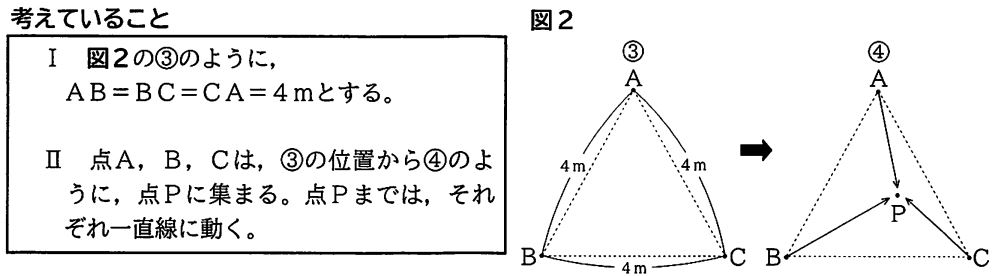
2人は、点A,B,Cが動く距離の合計が、最も短くなる点Pの位置を求めるにはどうしたらよいか先生に質問したところ、アドバイスをもらいました。
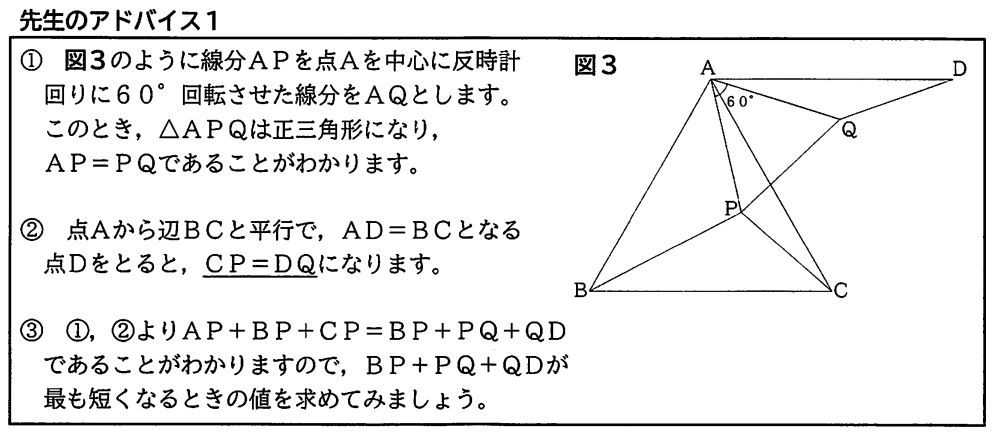
（2）下線部のCP＝DQであることを証明しなさい。
（3）点A,B,Cが動く距離の合計が最も短くなるときの値を求めなさい。
さらに2人は、先生から次のアドバイスをもらいました。
先生のアドバイス2の①をもとに作図すると、点Pは、3つの頂点から等距離にあることがわかりました。
図4の三角形ABCは正三角形で、点Pは正三角形の3つの頂点からの距離の合計が最も短くなる点です。また、△BCTはｍＣＢ＝ＣＴの二等辺三角形でＢＣ＝２ＢＴです。
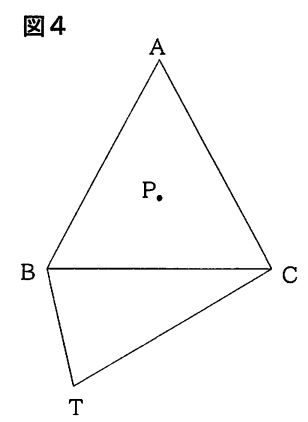
（4）先生のアドバイス2をもとに、3点Ｂ，Ｃ，Ｔからの距離が最も短くなる点Ｒをコンパスと定規を使って作図しなさい。ただし、作図に使った線は消さないこと。
解答・解説
（1） 【正答 2π㎝】
点B、点Cはそれぞれ、円周の1/4分だけ動くので、あわせて半円分動くことになる。
この円の円周は、2×2×π＝4π
これの半分なので、2π
（2） 【(例)
△APQ、△ABCは正三角形より
AP＝AQー①、AC＝BCー②、∠PAQ＝∠BCA＝60°ー③
AD//BCだから∠BCA＝∠DAC(錯角)
よって③より∠DAC＝60°ー④
△APCと△AQDについて、
③より∠PAC＝∠PAQ－∠CAQ＝60°－∠CAQ
④より∠QAD＝∠CAD－∠CAQ＝60°－∠CAQ
よって、∠PAC＝∠QADー➄
また、AD＝BCだから②よりAC＝ADー⑥
①、➄、⑥より2組の辺とその間の角が等しいので△APC≡△AQD
合同な2つの三角形の対応する辺の長さは等しいのでCP＝DQ】
（3） 【正答 4√3ｍ】
線分BP、PQ、QDの直線が一直線になるとき、BP∔PQ∔QDが最も短くなる。
△ABCより、BC＝AB＝4㎝
AD＝4㎝なので、△ABDはAB＝ADの二等辺三角形 ー①
また、AD＝BCかつAD//BCなので四角形ABCDは平行四辺形 ー②
①、②より四角形ABCDはひし形とわかる
線分ACと線分BDの交点を点Oとすると、
∠AOC＝90°ー③
また、△ABCは正三角形なので∠BAC＝60°ー④
③、④よりAB：BO：OA＝2：√3：1
BO＝4×√3/2＝2√3
BD＝2×BO＝4√3
（4） 【正答】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストは、滋賀県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。
高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
