滋賀県の2023年3月実施の令和5年度（2023年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。

 滋賀県の公立高校入試情報はこちら

大問1

問題文

(1) 13+3×(-2)を計算しなさい。

(2) 13a-54aを計算しなさい。

(3) 次の等式を〔〕内の文字について解きなさい。
3x+7y=21

(4) 次の連立方程式を解きなさい。

2x+y=5x+3y=-1

(5) 9√3-√12を計算しなさい。

(6) 次の式を因数分解しなさい。
x²-2x-24

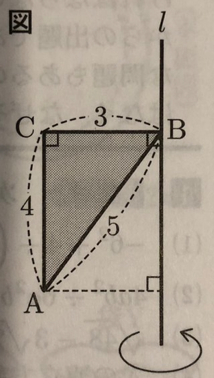
(7) 図の△ABCは、辺AB、BC、CAの長さがそれぞれ5、3、4の直角三角形です。この三角形を、直線lを軸として1回転させてできる回転体の体積を求めなさい。ただし、辺BCとlは垂直である。

(8) 下のデータは、ある生徒12人の先月読んだ本の冊数を調べ、冊数が少ない順に並べたものです。第3四分位数を求めなさい。
データ
【1 2 3 3 4 5 5 6 8 10 10 12】(冊)

(9) 3枚の硬貨を同時に投げるとき、2枚以上裏となる確率を求めなさい。ただし、硬貨は、表と裏のどちらかが出ることも同様に確からしいとする。

解答・解説

(1) 13+3×(-2)=13-6=7

(2) 1/3a-5/4a=4/12a-15/12a=4-15/12a=-11/12a

(3)
3x+7y=21
3x=-7y+21
x=-7/3y+7

(4) 2x+y=5x+3y=-1
2x+y=-1・・・➀、5x+3y=-1・・・②
➀の両辺に3をかけて、 6x+3y=-3・・・③
③-②をして、 x=-2
x=-2を➀に代入して、
-4+y=-1
y=3
よって、x=-2、y=3

(5) 9/√3-√12=9√3/3-2√3=3√3-2√3=√3

(6)
x²-2x-24=0
(x+4)(x-6)=0

(7)
2/3×(3×3×π)×4=24π

(8) 8+10/2=9(冊)

(9) 4/2×2×2=48=12

大問2

問題文

紙でふたのない容器をつくるとき、次の(1)から(4)までの各問いに答えなさい。ただし、紙の厚さは考えないものとする。

(1) 図1は正三角形です。底面にあたる正三角形DEFの1辺の長さを10√2㎝、辺ADの長さを10㎝とする容器をつくります。図2の線分の長さを10㎝とするとき、底面にあたる正三角形DEFをコンパスと定規を使って作図しなさい。ただし、作図に使った線は消さないこと。

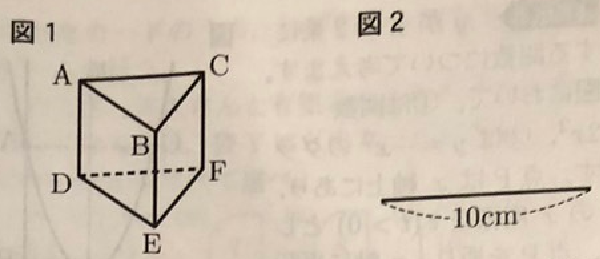
(2) 図3のような紙コップを参考に、容器をつくります。紙コップをひらいたら、図4のような展開図になります。図4において、側面にあたる辺ABと辺A’B’をそれぞれ延ばし、交わった点をOとすると、弧BB’、線分OB、線分OB’で囲まれる図形が中心角45°のおうぎ形になります。このとき、弧AA’の長さを求めなさい。

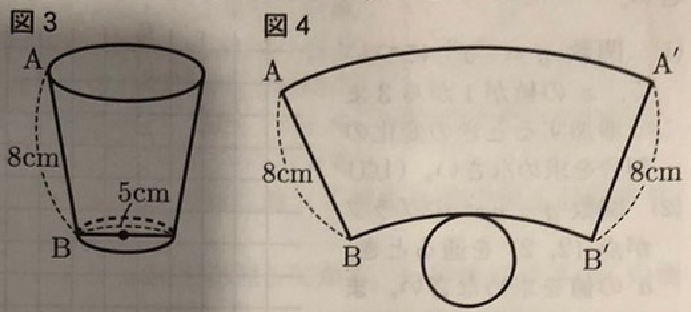
(3) 図5のような、長方形の紙があります。この紙の4すみから、図6のように1辺が、x㎝の正方形を切り取り、縦の長さを8㎝、横の長さを12㎝の長方形を底面とする図7のような直方体をつくります。図5の長方形の紙の面積と、図6の斜線部の長方形の面積の比が、2：1になるとき、xの長さを求めなさい。ただし、xの長さを求めるための方程式をつくり、答えを求めるまでの過程も書きなさい。

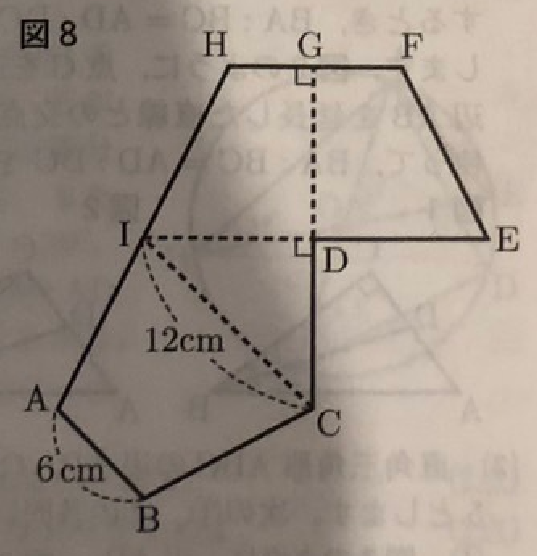
(4) 図8は容器の展開図です。辺AB、ICの長さはそれぞれ6㎝、12㎝とします。また、DC=DE=DG=DI=HF、GF=GH=、AI=HI=BC=FE、CG⊥HF、CG⊥IE、AB//ICとします。この展開図を組み立てたとき、辺ABとねじれの位置にある辺をすべて答えなさい。ただし、組み立てたときに重なる辺は、どちらか一方の辺を書くこととします。

解答・解説

(1) 省略

(2)
弧BB’の長さは図3の紙コップの底面の円の円周の長さと等しいから、
弧BB’=5π(㎝)
よって、
2×OB×π×45/360=5π
1/4OB=5
OB=20(㎝)
したがって、弧AA’の長さは
AA’=2π×(20+8)×45/360=2π×28×1/8=7π(㎝)・・・(A)

(3)
(図5の長方形の紙の面積)=(8+2x)×(12+2x)=4(x+4)(x+6)
(図6の斜線部の長方形の面積)=8×12=96
よって、
4(x+4)(x+6)：96=2：1
4(x+4)(x+6)=96×2
(x+4)(x+6)=48
x²+10x+24=48
x²+10x-24=0
(x+12)(x-2)=0
x=-12、2
ここで、x>0なので、x=2(㎝)・・・(A)

(4) 辺DI、DG、CD(ED)

大問3

問題文

yがxの2乗に比例する関数について考えます。図において、➀は関数y=2x²、②はy=-x²のグラフです。点Pはx軸上にあり、点Pのx座標をt(t>0)とします。点Pを通り、y軸に平行な直線と➀、②のグラフが交わる点を、それぞれA、Bとします。また、y軸について点Aと対称な点をCとします。次の(1)から(4)までの各問いに答えなさい。

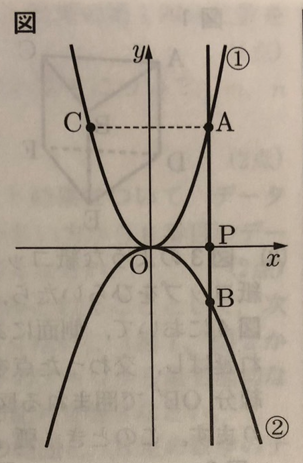
(1) 関数y=-x²について、xの値が1から3まで増加するときの変化の割合を求めなさい。

(2) 関数y=ax²のグラフが点(2,2)を通るとき、aの値を求めなさい。また、この関数のグラフをかきなさい。

(3) AB+ACの長さが1になるときのtの値を求めなさい。

(4) xの変域が-1≦x≦3のとき、関数y=2x²とy=bx+c(b<0)のyの変域が等しくなります。このとき、b、cの値を求めなさい。

解答・解説

(1) -9-(-1)/3-1=-8/2=-4

(2) グラフは省略
y=ax²に(2,2)を代入して、
2=4a
a=12

(3)
点Pのx座標がtのとき、点A、B、Cそれぞれの座標は
A(t,2t²)、B(t,-t²)、C(-t,2t²)
よって、
AB=2t²-(-t²)=3t²
AC=t-(-t)=2t
したがって、
AB+AC=3t²+2t
とあらわせて、この値が1になるので、
3t²+2t=1
3t²+2t-1=0
(3t-1)(t+1)=0
t=13,-1
条件より、t>0なので、t=1/3・・・(A)

(4)
xの変域が-1≦x≦3のとき、関数y=2x²の変域は、 0≦y≦18
b<0なので、y=bx+cはx=-1のとき最大値18、x=3のとき最小値0をとる。
よって、(x,y)=(-1,18)、(3,0)をそれぞれ代入すると、
18=-b+c・・・➀
0=3b+c・・・②
となる。②-➀をすると
4b=-18
b=-9/2
これはb<0に適する。b=-4を➀に代入して、
18=9/2+c
36=9+2c
2c=27
c=27/2
したがって、b=-9/2、c=27/2・・・(A)

大問4

問題文

∠C=90°の直角三角形ABCについて、次の(1)、(2)の各問いに答えなさい。

(1) 図1のように、∠Bの二等分線と辺ACの交点をDとするとき、BA：BC=AD：DCが成り立つことを証明します。図2のように、点Cを通り、DBに平行な直線と、辺ABを延長した直線との交点をEとします。図2を使って、BA：BC=AD：DCを証明しなさい。

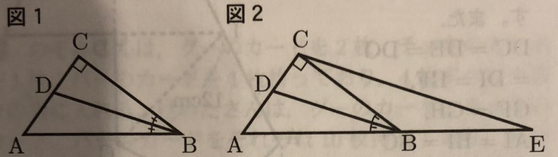
(2) 直角三角形ABCの辺AB、CAの長さをそれぞれ10、5とします。次の➀、②の各問いに答えなさい。

➀図3のように、辺ABの垂直二等分線をひき、辺AB、BCとの交点をそれぞれM、Nとします。このとき、△ABCと△NBMの面積比を求めなさい。

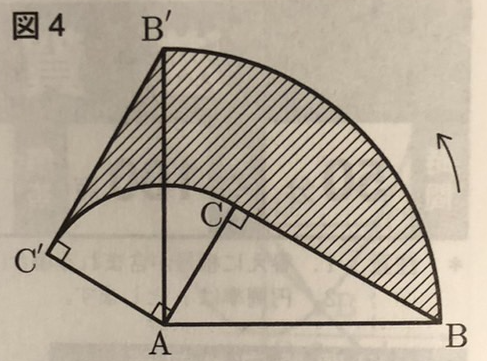
②図4のように、直角三角形ABCを頂点Aを中心に90°回転させます。このとき、辺BCが通過したときにできる傾斜部の面積を求めなさい。

解答・解説

(1)
DB//CEより、平行線の同位角は等しいので、
∠ABD=BEC
平行線の錯角は等しいので、
∠DBC=∠BCE
仮定より、∠ABD=∠DBC
以上より、∠BEC=∠BCE
2つの角が等しい三角形は二等辺三角形なので、
△BCEは二等辺三角形で、BE=BC・・・➀
△AECで、DB//CEより、AB：BE=AD：DC・・・②
➀②より、BA：BC=AD：DC

(2)
➀
△ABCについて、三平方の定理より、
BC²=10²-5²=100-25=75
BC=5√3
△ABC∽△NBMで、その相似比は BC：BM=5√3：5=√3：1
よって、△ABCと△NBMの面積比は (√3)²：1²=3：1・・・(A)

②
おうぎ形ABB’の面積は、 AB²×π×90/360=10²×π×1/4=25π
おうぎ形ACC’の面積は、 AC²×π×90/360=5²×π×1/4=25/4π
求める斜線部の面積は、 (おうぎ形ABB’+△AB’C)’-(おうぎ形ACC’+△ABC)
ここで、△AB’C’=△ABCより、求める面積は、
おうぎ形ABB’-おうぎ形ACC’=25π-25/4π=75/4π・・・(Ａ)

 滋賀県のその他の過去問を見る

志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！

家庭教師のやる気アシストは、滋賀県にお住まいの受験生のお子さんを毎年たくさん指導をさせ頂き、合格に導いています。
おかげさまで、昨年度の合格率は、関西エリア全体で97.3％という結果を残すことが出来ました。

高い合格率の秘訣は、指導経験豊富な先生の指導力に加え、1対1の指導でお子さん一人ひとりの状況に合わせた、お子さんだけのカリキュラムで勉強が進められるから！
家庭教師のやる気アシストは、お子さんの志望校合格まで全力でサポートさせて頂きます！

 アシストの受験対策をもっとみる

アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中

お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？

やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。