






島根県の2021年3月実施の令和3年度(2021年度)入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
問1 4ー12÷2を計算しなさい。
問2 方程式x²+8x+12 = 0 を解きなさい。
問3 連立方程式![]() を解きなさい。
を解きなさい。
問4 100gあたりa円の牛肉を300gと,100gあたりb円の豚肉を 500g買ったときの代金の合計が 1685 円 だった。この数量の関係を等式で表しなさい。ただし,すべての金額は消費税を含んでいるものとする。
問5 √8ー2/√2を計算しなさい。
問6 次のア~工の数の中で絶対値が最も大きいものを1つ選び,記号で答えなさい。
ア 2 イ √3 ウ -7/3 エ 0
問 7 y は x に反比例し,x=-4のとき y=2 である。xとyの関係を式に表しなさい。
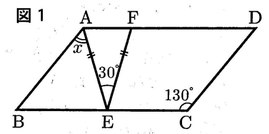
問8 図1のような平行四辺形ABCDにおいて,辺BC上に 点E,辺AD上に点 Fを,AE=EF,∠AEF= 30°となるようにとる。∠xの大きさを求めなさい。
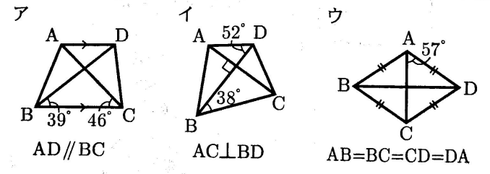
問9 次のア~ウの四角形 ABCD のうち, 4 点 A,B,C,Dが1つの円周上にあるものを1つ選び,記号で答えなさい。
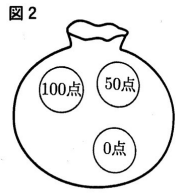
問10 図2のように100点,50点,0点と書いてある3個の玉が入った袋がある。袋の中から1個の玉を取り出して点数を調べて袋の中に戻し,もう一度1個の玉を取り出して点数を調べる。取り出した玉に書いてある点数の合計が50点以下になる確率を求めなさい。ただし,どの玉が取り出されることも同様に確からしいものとする。
問1 【正答 -2】
問2 【正答 x=-6,-2】
問3 【正答 x= 2, y= 3】
問4 【正答 3a+5b=1685】
問5 【正答 √2】
問6 【正答 ウ】
問7 【正答 y =-8/x】
問8 【正答 55度】
問9 【正答 イ】
問10 【正答 1/3】
次の問1,問2に答えなさい。
問1 1班と2班のそれぞれ10人に対してテストを実施したところ,点数が表のようになった。ただし点数は条件1を満たす。あとの1~3に答えなさい。
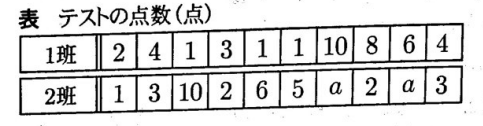
・点数は0点以上,10点以下の整数である。
・表中のaは同じ点数である。
・2班10人の点数の平均値は5.0点である。
1 1班10人の点数について,次の(1),(2)に答えなさい。
(1)中央値を求めなさい。
(2)平均値を求めなさい。
2 表中の点数aの値を求めなさい。
3 次の条件2を満たすように,1班のx点の生徒1人と2班のy点の生徒1人を入れかえた。このとき,x, yの値を求めなさい。
・1班10人の点数の平均値と2班10人の点数の平均値を等しくする。
・1班10人の点数の中央値を生徒を入れかえる前より大きくする。
問2 1,4,7,10,13,16,…のように1か ら3ずつ増える整数を図のように並べていく。下の1,2に答えなさい。
1 太郎さんは,図の2行目の5つの数の和を計算し,16 + 19 + 22 + 25 + 28 = 110 = 5 × 22 となった結果から,次のことが成り立つと予想した。
予想「各行の5つの数の和は,その行の3列目の数の5倍である。」
このことを,花子さんが,次のように説明した。 【ア】,【イ】に適する式を甚きなさい。また,【ウ】にその説明の続きを書き,説明を完成させなさい。
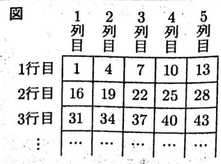
ある行の1列目の整数をnとすると,5つの数は小さい順に
n,【ア】,n+6,n+9,【イ】
と表せるわね。だから,
【ウ】
したがって,
「各行の5つの数の和は,その行の3列目の数の5倍である。」
という予想は正しそうね。
2 20行目の5つの数の和を求めなさい。
問1 1(1) 【正答 3.5点】
問1 1(2) 【正答 4.0点】
問1 2 【正答 a= 9】
問1 3 【正答 x=1,y=6】
問2 1 【正答 ア.n+3 イ.n+12 ウ.(例)この5つの数の和は,n + (n + 3) + (n + 6) + (n + 9) + (n + 12)= 5n + 30 = 5 (n + 6)より,3列目の数n+6の5倍である。】
問2 2 【正答 1460】
A中学校とB中学校には吹奏楽部があり,それぞれの中学校では毎月,活動費を支給する。ただし,中学校によって活動費の決め方は異なり,その決め方をまとめたものが,次の表である。
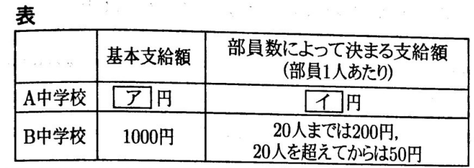
活動費は, 基本支給額と部員数によって決まる支給額の合計であり,基本支給額は,部員数が0人であっても必ず 支給される。
例えば,B中学校については,ある月の部員数が100人 のとき 基本支給額が1,000円であり, 部員数によって決まる支給額は20人までは1人あたり200円で,残りの80 人は1人あたり50円である。したがって, その月の活動費を求める式は,
1000 + 200 × 20 + 50 × 80
であり,これを計算すると,活動費は9000円になる。活動費と部員数の関係を一次関数を用いて考える。
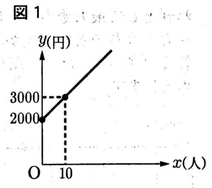
図1は,A中学校の吹奏楽部の部員数をx人,活動費をy円としたときのxとy の関係をグラフで表したものである。下の問1~問4に答えなさい。
問1 図1のグラフを利用して,表中の【ア】,【イ】にあてはまる値を求めなさい。
問2 A中学校の吹奏楽部の部員数が50人であったとき,その月の活動費を求めなさい。
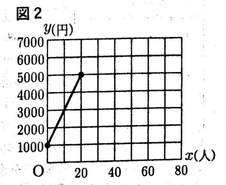
問3 図2は,B中学校の吹奏楽部の部員数をx人,活動費をy円 としたとき,0≦x≦20のときの Xとyの関係をグラフで表したものである
次の1,2に答えなさい。
1 x≧20のときのxとyの関係を表す式を求めなさい。
2 x≧20のときのxとyの関係を表すグラフを図 2にかき加えなさい 。
問4 A中学校とB中学校の吹奏楽部について,次の1,2に答えなさい。
1 活動費が等しく,部員数も等しくなる場合が2通りある。 その2通りの部員数を求めなさい。
2 活動費が等しく,部員数の差が20人となるときの活動費を求めなさい。
問1 【正答 ア.2000 イ.100】
問2 【正答 7000円】
問3 1 【正答 y = 50x+ 4000】
問3 2 【正答 】
問4 1 【正答 10人と40人】
問4 2 【正答 8000円】
関数y=1/2x²…①のグラフ上に2点A, Bがあり,そのx座標はそれぞれー2,4 である。次の問1,問 2 に 答えなさい。
問1 図1 のように,2点A,Bを通る直線をlとし,lとy軸との交点をCとする。下の1~3に答えなさい。
1 関数①について,xの変数が-2≦x≦4のとき,yの変域を求めなさい。
2 点Cのy座標を求めなさい。
3 △OABの面積 を求めなさい。
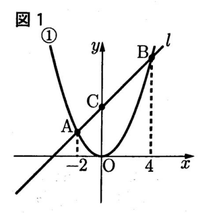
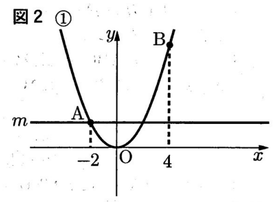
問2 図2のように,点A を通りx軸に平行な直線をmとする。下の1,2に答えなさい。
1 m上に△OABの面積と△OAPの面積が等しくなるような点Pをとるとき,点Pの座標を求めなさい。ただし,点Pのx座標は正であるとする。
2 問2 の1の点P に対して,四角形OABPを考える。辺BP上に点Q をとり,△ABQ の面積が四角形OABP の面積 の1/2となるように したい。点Qの座標を求めなさい。
問1 1 【正答 0 ≦y≦8】
問1 2 【正答 4】
問1 3 【正答 12】
問2 1 【正答 P (10, 2)】
問2 2 【正答 Q (8, 4) 】
図1のように,∠C=90°の直角三角形ABCがあり,BC=a,CA=b,AB=cとするとき,次の関係が成り立つ。
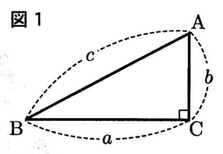
a²+b²=c²…[1](三平方の定理)
下の問1~問4に答えなさい。
問1 a=3,b=1のとき[1]が成り立つような正の数Cの値を求めなさい。
問2 次の長さを3辺とする三角形のうち,直角三角形はどれか。ア~ウから1つ選び,記号で答えなさい。
ア 2㎝,3㎝,4㎝
イ 3㎝,4㎝,5㎝
ウ 4㎝,5㎝,6㎝
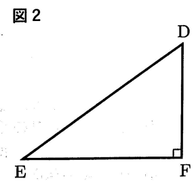
問3 図2の∠F = 90°の直角三角形 DEFにおいて,辺DE上に∠DGF = 90° となる点Gをとるとき,点Gの位置を 定規とコンパスを用いた作図で求め, 文字Gを書きなさい。ただし,作図に用いた線は消さないでおくこと。
問4 図3のように, 図1の直角三角形 ABC の辺 AB 上に∠ARC= 90° となる点 Hをとる。 次の1, 2に答えなさい。
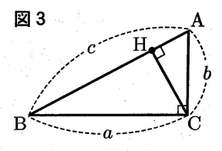
1 △ACH∽△CBHであることを証明しなさい。
2 ヒカルさんは,△ABC,△ACH,△CBHがすべて相似であることに気がつき,3つの三角形の面積の関係を用いて,[1](三平方の定理)が成り立つことを次のように説明した。
【ア】~【カ】にあてはまる文字や式を入れて,説明を完成させなさい。
△ABC, △ACH, △CBH の面積をそれぞれP, Q, Rとすると,
Q+R=P… ①
が成り立ちます。
ここで,△ABCと△ACHの相似比は,c:bであるから,△ABC と△ACH の面積の比は,
P:Q=【ア】:【イ】
この比例式を変形して,Qについて解くと,
Q=【ウ】×P…②
また,△ABC と△CBH の相似比は,
【エ】:【オ】であるから, 同様に考えると,
R=【カ】×P…③
そして,②,③を①に代入してできた式を変形すると,[1]が成り立ちます。
問1 【正答 c=√10】
問2 【正答 イ】
問3 【正答 】
問4 【正答 (例)
△ACHと△CBHにおいて,
∠AHC=∠CHB=90°…①
∠ACH+∠BCH= 90°より,
∠ACH=90°-∠BCH
∠CBH+∠BCH= 90°より,
∠CBH= 90°-∠BCH】
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています!
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…?」とご質問いただくことも多いですが、ご安心ください!家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです!
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます!
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか?
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか?
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。

