【徳島県】令和3年度/2021年度入学者高校入試選抜試験：数学
徳島県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の（1）～（10）に答えなさい。
（1）12÷(-4)を計算しなさい。
（2）√3×√8を計算しなさい。
（3）(x -4)(x -5)を展開しなさい。
（4）二次方程式x²-5x+3=0を解きなさい。
（5）ジョーカーを除く1組52枚のトランプをよくきって，そこから1枚をひくとき，1けたの偶数の札をひく確率を求めなさい。ただし，トランプのどの札をひくことも，同様に確からしいものとする。
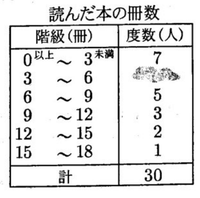
（6）表は，ある中学校の生徒30人が1か月に読んだ本の冊数を調べて，度数分布表に整理したものである。ただし，一部が汚れて度数が見えなくなっている。この度数分布表について，3冊以上6冊未満の階級の相対度数を求めなさい。
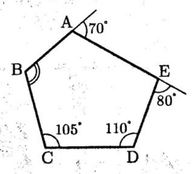
（7）図のように，五角形ABCDEがあり，∠BCD = 105°，∠CDE = 110°である。また，頂点Ａ，Eにおける外角の大きさがそれぞれ70°，80°であるとき，∠ABCの大きさを求めなさい。
（8）一次関数y = 5/2x + aのグラフは，点（4，3）を通る。このグラフとy軸との交点の座標を求めなさい。
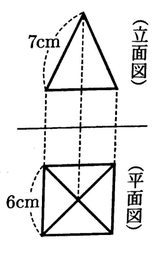
（9）図は，正四角錐の投影図で ある。この正四角錐の体積を求めなさい。
（10）336/nの値が，ある自然数の2乗となるような自然数nのうち，最も小さいものを求めなさい。
解答
（1） 【正答 -3】
（2） 【正答 2√6】
（3） 【正答 x² – 9x + 20】
（4） 【正答 x = 5±√13 / 2】
（5） 【正答 4/13】
（6） 【正答 0.4】
（7） 【正答 115度】
（8） 【正答 （0，-7）】
（9） 【正答 24√10㎤】
（10） 【正答 21】
大問2
問題文
中学生のみきさんたちは，職場体験活動を 行った。みきさんは，ゆうさんと一緒にスーバーマーケットで活動することになり，野菜売り場の特設コーナーで袋詰め作業や販売の手伝いをした。その日，特設コーナーでは，玉ねぎ3個を1袋に入れて190円，じゃがいも6個を 1袋に入れて245円で販売した。次は，活動後の2人の会話の一部である。（1）・（2）に答えなさい。ただし，消費税は考えないものとする。
みきさん 今日，特設コーナーでは，玉ねぎとじゃが いもが合わせて91袋売れ，その売上金額の合計は 19380円だった，と店長さんが言っていましたね。
ゆうさん はい。 91袋売れたということですが，玉ねぎとじゃがいもは，それぞれ何個売れたのでしょうか。
みきさん 数量の関係から連立方程式をつくって求めてみましょう。
（1）玉ねぎとじゃがいもが，それぞれ何個売れたかを求めるために，みきさんとゆうさんは，それぞれ 次のように考えた。【みきさんの考え方】の[ア]・ [イ]，【ゆうさんの考え方】の[ウ]・ [エ]にあてはまる式を，それぞれ書きなさい。
【みきさんの考え方】
玉ねぎ3個を入れた袋がx袋，じゃがいも6個を入れ た袋がy袋売れたとして，連立方程式をつくると，
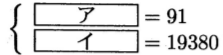
これを解いて，問題にあっているかどうかを考え，そ の解から，玉ねぎとじゃがいもが，それぞれ何個売れたかを求める。
【ゆうさんの考え方】
玉ねぎがx個，じゃがいもがy個売れたとして，連立方程式をつくると，
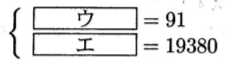
これを解いて，問題にあっているかどうかを考え，玉ねぎとじゃがいもが，それぞれ何個売れたかを求める。
（2）玉ねぎとじゃがいもは，それぞれ何個売れたか，求めなさい。
解答
（1）ア 【正答 x+y】
（1）イ 【正答 190x+245y】
（1）ウ 【正答 x/3+y/6】
（1）エ 【正答 190/3x+245/6y】
（2） 【正答 玉ねぎ159個，じゃがいも228個】
大問3
問題文
あゆみさんの中学校では，体育祭で学年ごとにクラス 対抗の応援合戦が行われる。(1)・(2)に答えなさい。
（1）3年生の応援合戦は，A組，B組，C組，D組の4クラスが1クラスずつ順に行う。応援合戦を行う順序のうち，A組がB組より先になるような場合は何通りあるか，求めなさい。
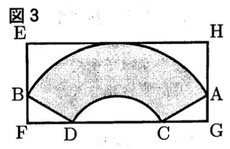
（2）あゆみさんのクラスでは，図1のように，おうぎ形に 切った厚紙を応援合戦で使 うことにした。これは，図2 のように，半径24cm，中心角120°のおうぎ形OABの厚紙に，おうぎ形OABから半径12cm，中心角120° のおうぎ形OCDを取り除いた図形ABDCを色画用紙で作って貼ったものである。(a)・(b)に答えなさい。
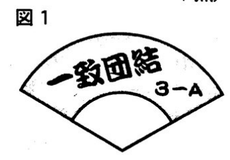
（a）あゆみさんたちは，図2のABに沿って飾りをつけることにした。ABの長さは何cmか，求めなさい。ただし， 円周率はπとする。
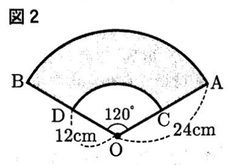
（b）あゆみさんたちは，図形ABDCをぴったり切り抜くことができる長方形の大きさを調ベてみることにした。図3のように，図形ABDCのABが辺EHに接し，点Aが辺HG上，点ABが辺EF上，2点C,Dが辺FG上にそれぞれくるように，長方形EFGHをかくとする。長方形EFGHのEF,FGの長さは，それぞれ何cmか，求めなさい。
解答
（1） 【正答 12通り】
（2）（a） 【正答 16πcm】
（2）（b） 【正答 EF18cm，FG24√3】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
図1，図2のように，2つの関数y = 1/2x²とy = x + 12のグラフが2点A，Bで交わっている。点Aのx座標は-4，点Bのx座標は6である。（1）・（2）に答えなさい。
（1）図1について，(a)・(b)に答えなさい。
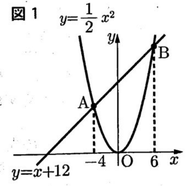
（a）点 A のy座標を求めなさい。
（b）関数y= x + 12のグラフとx軸について線対称となるグラフの式を求めなさい。
（2）図2のように，関数y = 1/2x²のグラフ上を点Aから点Bまで動く点Pをとり，点Pから平行な直線をひき，関数y = x + 12のグラフとの交点をQとする。また，点P, Qからの軸へ垂線をひき，の軸との交点をそれぞれ R, Sとする。(a) ・ (b)に答えなさい。
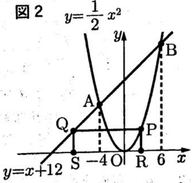
（a）点Pのの座標が2のとき，原点を通り，長方形 PQSRの面積を2等分する直線の式を求めなさい。
（b）長方形PQSRが正方形になるときのPRの長さをすべて求めなさい。
解答
（1）（a） 【正答 8】
（1）（b） 【正答 y = -x -12】
（2）（a） 【正答 y = – 1/4 x】
（2）（b） 【正答 9/2，8】
大問5
問題文
図のように，AB= 2 cm, AD = 4 cm の長方形ABCDがある。線分BCを延長した直線上に，∠BDE= 90°となるように点Eをとり，2点D,Eを結ぶ線分AEと線分BDとの交点をF，線分AEと線分CDとの交点をGとするとき，(1)・(4)に答えなさい。
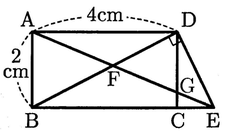
（1）∠AFD = a°とする。∠DEGの大きさをaを用いて表しなさい。
（2）△ABD∽△DEBを証明しなさい。
（3）頂点Dから線分AEにひいた垂線と線分 AEとの交点をHとする。線分DHの長さを求めなさい。
（4）四角形BCGFの面積を求めなさい。
解答
（1） 【正答 (a – 90)度】
（2） 【正答 （例）△ABDと△DEBで，
仮定より，LBAD= LEDB = 90°…①
AD II BEから， 平行線の錯角は等しいので，
∠ADB＝∠DBE…②
①，②から，2組の角が，それぞれ等しいので，
△ABD∽△DEB】
（3） 【正答 8√29/29㎝】
（4） 【正答 166/45㎠】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
