【徳島県】令和4年度/2022年度入学者高校入試選抜試験：数学
徳島県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の（1）～（10）に答えなさい。
（1）-7-(-3)を計算しなさい。
（2）15×(5x-2y)/6を計算しなさい。
（3）a<√30となる自然数aのうち、最も大きいものを求めなさい。
（4）二次方程式3x²-36=0を解きなさい。
（5）1個aｇのゼリー6個を、bｇの箱に入れたときの全体の重さは800ｇ未満であった。この数量の関係を不等式で表しなさい。
（6）yはxに反比例し、x=4のときy=5/4である。xとyの関係を式に表しなさい。
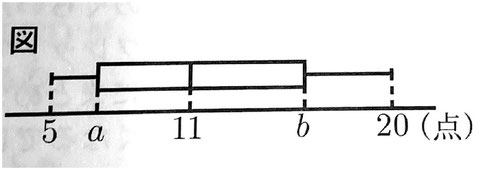
（7）次の表は、クイズ大会に参加した11人の得点である。この表をもとにして、箱ひげ図を書くと、次の図のようになった。a,bの値をそれぞれ求めなさい。
表
13,7,19,10,5,11,14,20,7,8,16
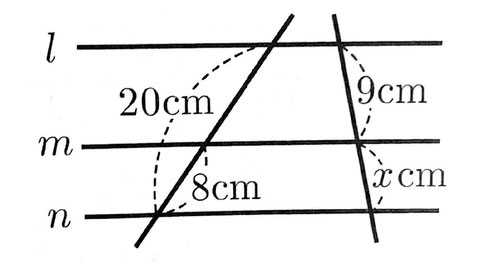
（8）次の図のように、平行な3つの直線l,m,nがある。xの値を求めなさい。
（9）1から6までの目が出る大小2つのさいころを同時に投げるとき、出る目の数の和が素数になる確率を求めなさい。ただし、それぞれのさいころについて、どの目が出ることも同様に確からしいものとする。
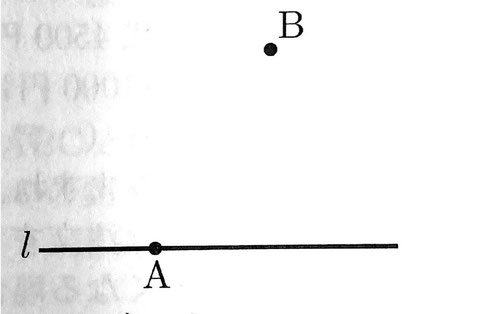
（10）次の図のように、直線lと直線l上の点A、直線l上にない点Bがある。点Aで直線lに接し、点Bを通る円の中心Oを、定規とコンパスの両方を使って次の図に作図しなさい。ただし、作図に使った線は消さずに残しておくこと。また、定規やコンパスを持っていない場合は、作図の方法を文章で書きなさい。
解答
【解答】
（1） 【正答 -4】
（2） 【正答 15x-6y】
（3） 【正答 5】
（4） 【正答 x =±2√3】
（5） 【正答 6a+b<800】
（6） 【正答 y=5/x】
（7） 【正答 a=7,b=16】
（8） 【正答 x=6】
（9） 【正答 5/12】
（10） 【正答 下記参照】
【解説】
（1） （与式）=-7+3=-4
（2） （与式）=3×(5x-2y)=15x-6y
（3） √5²<√30<√6²より5<√30<6であるから、求める自然数は5
（4） 3x²=36 x²=12 x=±√12 x=±2√3
（6） a=4×5/4=5 したがって、y=5/x
（7） 11人の得点を小さい方から順に並べると「7,7,8,10,11,13,14,16,19,20」。図のa,bはそれぞれ第1四分位数と第3四分位数を表しているから、a=7,b=16である。
（8） 平行線と比の性質から、8:(20-8)=x:9 2:3=x:9 よって、x=6である。
（9） 和が素数になるのは次の15通り。(1,1)(1,2)(2,1)(1,4)(2,3)(3,2)(4,1)(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)(5,6)(6,5)。したがって求める確率は15/36=5/12
（10） 以下に文章記述
①点Aを中心とする円を書き、直線lとの2交点をそれぞれ中心として、等しい半径の円をかく。この2円の交点とAを通る直線をひく。
②点A,Bをそれぞれ中心として、等しい半径の円をかき、この2円の交点を通る直線をひく。
③①、②でひいた2直線の交点が中心Oである。
大問2
問題文
かずきさんとみさきさんは、厚紙を切って、3種類の図形A,B,Cをたくさん作っている。図形Aは正方形、図形Bは1辺の長さが図形Aの1辺の長さと等しく、他方の辺の長さが1ｃｍの長方形、図形Cは1辺の長さが1ｃｍの正方形である。（1）、（2）に答えなさい。
（1）厚紙は、赤、青、白、黄、緑の5色ある。この5色から3色を選ぶとき、その選び方は全部で何通りあるか、求めなさい。
（2）2人は、図形A,B,Cを何枚か組み合わせて、重ならないようにすきまなくしきつめ、いろいろな四角形をつくろうと考えている。図形Aの1辺の長さをxｃｍとして、(a)～(c)に答えなさい。
(a)図形Aを1枚、図形Bを3枚、図形Cを2枚の合計6枚を組み合わせると、1つの長方形をつくることができる。x=3のとき、この長方形の2辺の長さは、それぞれ何ｃｍか、求めなさい。
(b)かずきさんは、図形Aを1枚、図形Bを6枚、図形Cを8枚の合計15枚を組み合わせて、1つの長方形をつくった。この長方形の周の長さをxを用いて表しなさい。
(c)みさきさんは、図形A,B,Cを何枚か組み合わせて、1辺の長さが(x+7)ｃｍの正方形を1つつくった。この正方形の面積は、図形Aを1枚、図形Bを6枚、図形Cを8枚の合計15枚を組み合わせてかずきさんが作った1つの長方形の面積より105ｃｍ²大きかった。このとき、xの値を求めなさい。
解答
【解答】
（1） 【正答 10通り】
（2）(a) 【正答 4ｃｍ、5ｃｍ】
（2）(b) 【正答 (4x+12)ｃｍ】
（2）(c) 【正答 x=8】
【解説】
（1） 求める場合の数は選ばない2色を選ぶ場合の数と等しいので、10通り。
（2）(a) 求める長方形は次の図のようになる。したがって、x=3のとき、縦4ｃｍ、横5ｃｍ
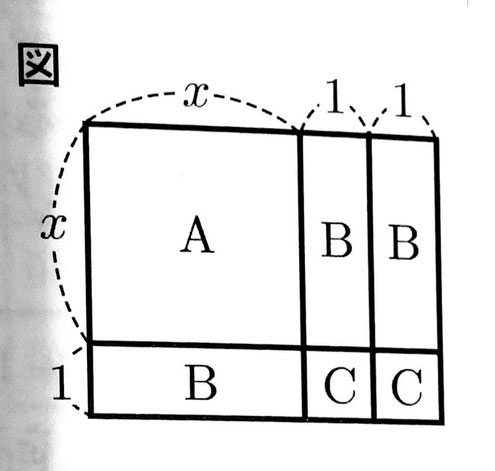
（2）(b) A,B,Cの図形の面積はそれぞれx²ｃｍ²、xｃｍ²、1ｃｍ²。よって、長方形の面積はx²+6x+8と表せる。x²+6x+8=(x+2)(x+4)であるから、求める長方形の周の長さは、2(x+2)+2(x+4)=4x+12（ｃｍ）
（2）(c) みさきさんのつくった正方形の面積は(x+7)²ｃｍ²、かずきさんのつくった長方形の面積は(x²+6x+8)ｃｍ²であるから、xについての方程式(x+7)²=(x²+6x+8)+105を解いて、x=8
大問3
問題文
高校生のあおいさんは、部活動でおそろいのTシャツをつくることになり、どの会社に注文するかについて、まことさんと相談している。次は、2人の会話の一部である。（1）、（2）に答えなさい。ただし、消費税は考えないものとする。
【会話の一部】
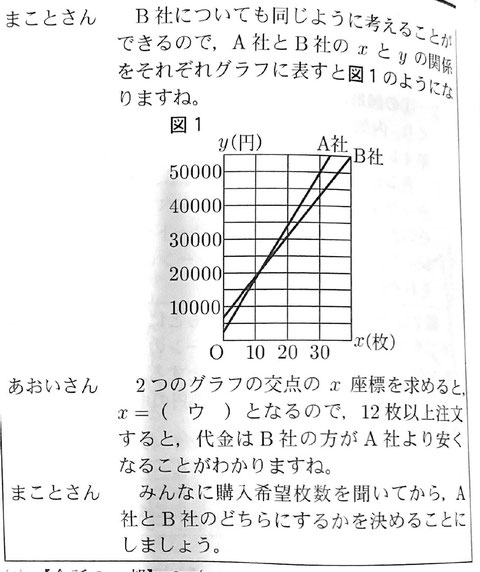
（1）【会話の一部】の（ア）・（ウ）にあてはまる数を、（イ）にはあてはまる式を、それぞれ書きなさい。
（2）相談した結果、あおいさんたちはB社に注文しようと考えていたが、インターネットでC社を見つけた。下の表2は、C社の料金についてまとめたものである。(a)・(b)に答えなさい。
(a)C社に25枚注文するときの代金を求めなさい。
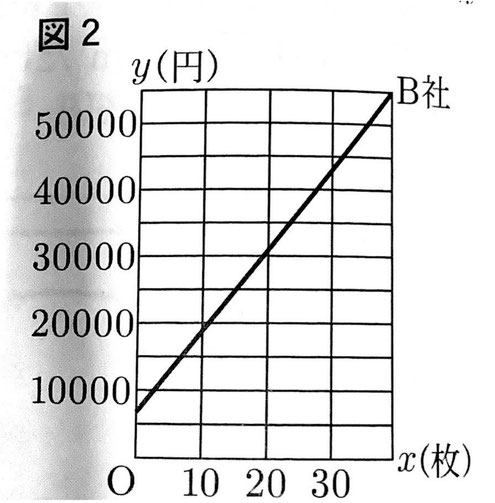
(b)まことさんは、何枚以上注文するとC社の方がB社より代金が安くなるかについて、次のように説明した。図2には、B社のグラフがかかれている。C社のグラフを考え、【まことさんの説明】の（エ）・（オ）にあてはまる言葉を、（カ）・（キ）にはあてはまる数をそれぞれ書きなさい。
解答
【解答】
（1） 【正答 ア：13000 イ：1500x+3500 ウ：35/3】
（2）（a） 【正答 39000円】
（2）（b） 【正答 エ：平行 オ：上 カ：30 キ：31】
【解説】
（1）ア 基本料金7000円とTシャツ代4000円、プリント代2000円で合計7000+4000+2000＝13000（円）
（1）イ y＝3500+900x+600xより、y＝1500x+3500
（1）ウ B社についてxとyの関係を式に表すとy=1200x+7000だから、連立方程式y=1500x+3500…①、y=1200x+7000…②を解くと、1500x+3500=1200x+7000 x=35/3
（2）（a） 基本料金11,000円とTシャツ代(800×25)円、プリント代(400×20)円の合計は11000+20000+8000=39000（円）
（2）（b） グラフは下図のようになる。
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
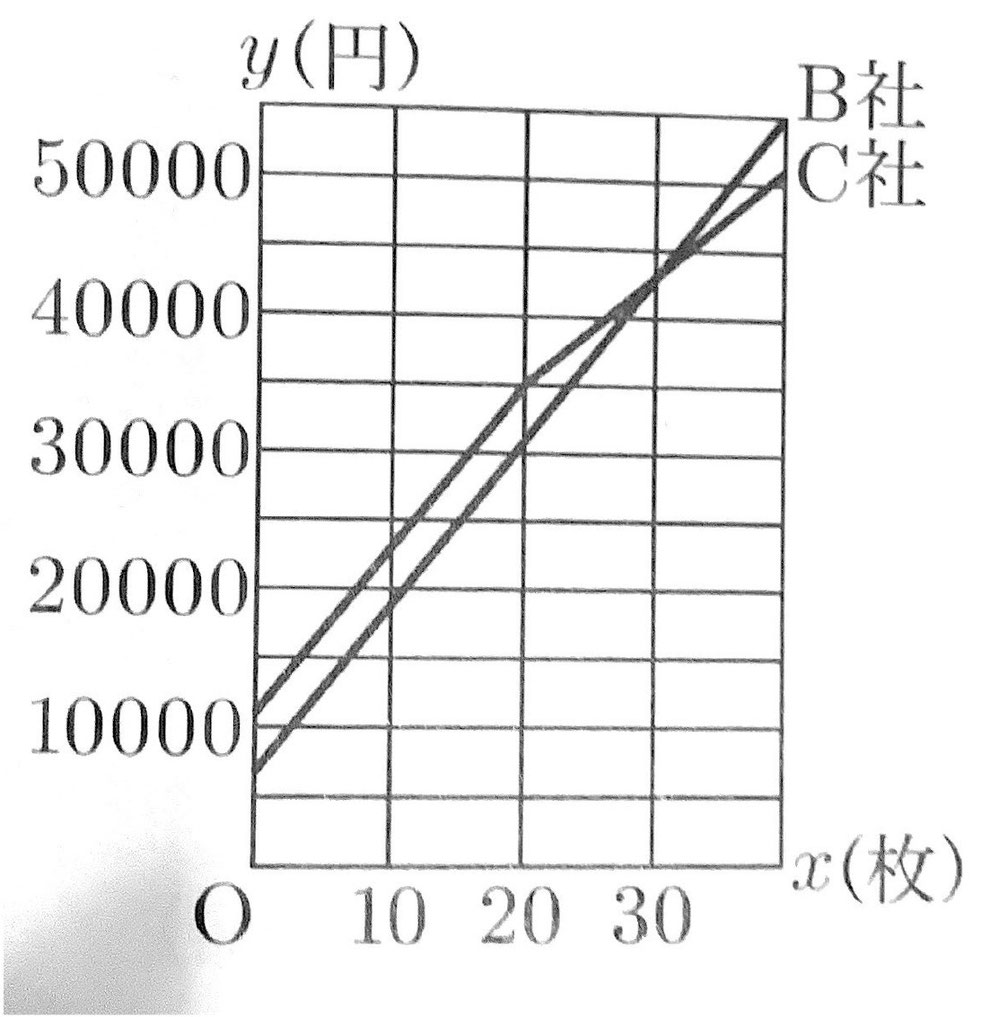
次の図のように、関数y=ax²(a>0)のグラフ上に2点A,Bがあり、点Aのｘ座標は-4、点Bのｘ座標は2である。また、直線ABとｙ軸との交点をCとする。（1）～（3）に答えなさい。
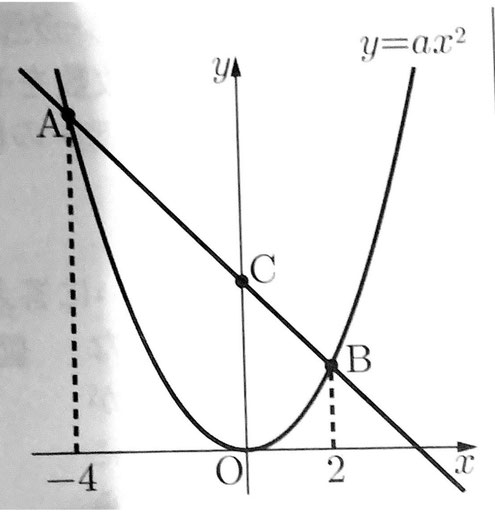
（1）点Aのｙ座標が6のとき、点Oを回転の中心として、点Aを点対称移動した点の座標を求めなさい。
（2）a=1/2のとき、線分ABの長さを求めなさい。
（3）a=1のとき、(a)・(b)に答えなさい。
(a)△OABの面積を求めなさい。
(b)線分ACの中点をPとし、点Qを関数y=ax²のグラフ上にとる。△OABと△OPQの面積が等しくなるときの点Qのｘ座標を求めなさい。ただし、点Qのｘ座標は正とする。
解答
【解答】
（1） 【正答 （4，-6）】
（2） 【正答 6√2】
（3）（a） 【正答 24】
（3）（b） 【正答 -3+√33】
【解説】
（1） A（-4，6）より、求める座標は（-(-4),-6）＝（4，-6）
（2） 放物線の式はy=1/2x²となるから、点A,Bの座標はそれぞれA（-4，8）、B（2，2）となる。よって、AB＝√｛2-（-4）｝²+（8-2）²＝√36+36＝6√2
（3）（a） 放物線の式はy=x²となるから、点A,Bの座標はそれぞれA（-4，16）、B（2，4）となる。よって、直線ABの式は、y=-2x+8であるから、点Cの座標はC（0，8）となる。△OAB＝△AOC+△BOC＝1/2×8×4+1/2×8×2＝24
（3）（b） 点Pの座標は（-4+0/2，16+8/2）＝（-2，12）また△OAB＝△OPRとなるようにｙ軸上に点Rをとり、ｙ座標を正とすると、R（0，24）となる。求める点Qは、Rを通り直線OP：y=-6xに平行な直線y=-6x+24と放物線y=x²との交点であるから、x²=-6x+24を整理して、x²+6x-24=0 したがって、x=-3±√33 x>0より、点Qのｘ座標はx=-3+√33
大問5
問題文
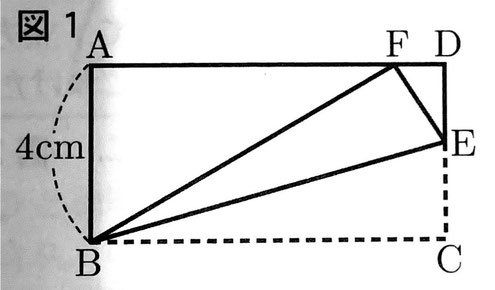
図1、図2のように、AB＝4ｃｍ、AB<ADである長方形ABCDを、ある線分を折り目として折り返したものがある。（1）、（2）に答えなさい。
（1）図1のように、長方形ABCDを、辺CD上の点Eと頂点Bを結んだ直線BEを折り目として、頂点Cが辺AD上にくるように折り返したとき、頂点Cが移る点をFとする。(a)・(b)に答えなさい。
(a)∠ABF＝50°のとき、∠BEFの大きさを求めなさい。
(b)DE:EC=7:9のとき、線分EFの長さを求めなさい。
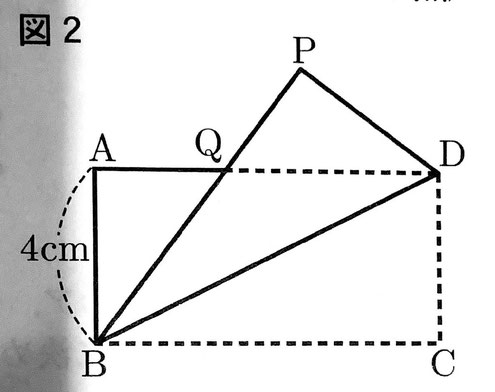
（2）図2のように、長方形ABCDを、対角線BDを折り目として折り返したとき、頂点Cが移る点をP、辺ADと線分BPとの交点をQとする。(a)・(b)に答えなさい。
(a)△ABQ≡△PDQを証明しなさい。
(b)対角線BDの中点をR、線分ARと線分BPとの交点をSとする。AD＝12ｃｍのとき、四角形RDPSの面積は△BRSの面積の何倍か、求めなさい。
解答
【解答】
（1）(a) 【正答 70度】
（1）(b) 【正答 9/4ｃｍ】
（2）(a) 【正答 下記参照】
（2）(b) 【正答 21/5倍】
【解説】
（1）(a) ∠FBE＝1/2∠FBC＝1/2（90°-∠ABF）＝20° ∠BEF＝180°-（90°+∠FBE）＝70°
（1）(b) EF＝xｃｍとすると、EF＝EC＝xｃｍ DE:EC＝7:9より、（4-ｘ）：ｘ＝7：9 ｘ＝9/4
（2）(a)
△ABQと△PDQで、四角形ABCDは長方形であり、対角線BDで折り返しているから、
AB＝PD…① ∠BAQ＝∠DPQ…②
対頂角は等しいので、∠AQB＝∠PQD…③
三角形の内角の和が180°であることと②、③より、
∠ABQ＝∠PDQ…④
①、②、④から、1組の辺とその両端の角がそれぞれ等しいから、△ABQ≡△PDQ
（2）(b) AQ＝xｃｍとすると、QD＝QB＝（12-x）ｃｍと表せる。△ABQについて三平方の定理より、4²+ｘ²＝（12-ｘ）² これを解いて、x＝16/3 よって、AQ＝16/3ｃｍ、QD＝20/3ｃｍとなる。これより、△AQP∽△DQBで相似比は4：5となるから、AP：BD＝4：5 また、点RはBDの中点であるからBD：BR＝2：1
これらより AP：BR＝8：5で、△ASP∽△RSBであるから、AS：RS＝8：5となる。したがって、△BRS＝5/13△ABR＝5/13×（1/4×4×12）＝60/13（ｃｍ²）
また、四角形RDPS＝△BDP-△BRS＝（1/2×4×12）-60/13＝252/13（ｃｍ²）
よって、四角形RDPS：△BRS＝252/13：60/13＝21：5であるから、四角形RDPSは△BRSの21/5倍である。
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
