【鳥取県】令和3年度/2021年度入学者高校入試選抜試験：数学の解説
鳥取県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
1 次の計算をしなさい。
（1） 3+(-5)
（2） -2/3×(-3/4)
（3） 5√6-√24+18/√6
（4） 3(x+y)-2(-x+2y)
（5） -4ab²÷(-8a²b)×3a²
2 (3x-y)²を展開しなさい。
3 a=-3のとき、a²+4aの値を求めなさい。
4 x²+5x-6を因数分解しなさい。
5 一次方程式5-3x/2-x-1/6=1を解きなさい。
6 二次方程式x²-x-1=0を解きなさい。
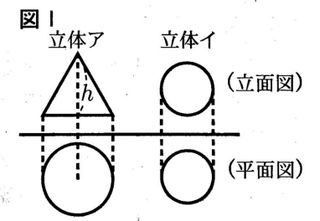
7 図Ⅰは2つの立体の投影図である。立体アと立体イは、立方体、円柱、三角柱、円錐、三角錐、球のいずれかであり、2つの立体の体積は等しい。平面図の円の半径が、立体アが4㎝、立体イが3㎝のとき、立体アの高さhの値を求めなさい。
8 関数y＝ax²のグラフが点(6,12)を通っている。このとき、次の（1）,（2）に答えなさい。
（1）aの値を求めなさい。
（2）xの変域が-4≦x≦2のとき、yの変域を求めなさい。
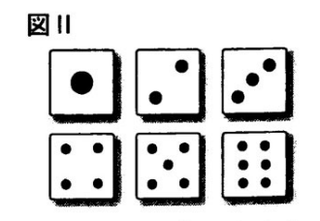
9 図Ⅱのような1～6までの目がある1個のさいころを2回投げて、1回目に出た目をa,2回目に出た目をbとする。このとき、積abの値が12未満となる場合と12以上となる場合とでは、どちらの方が起こりやすいか、次のア～ウからひとつ選び、記号で答えなさい。また、そのように判断した理由を、確率を計算し、その値を用いて説明しなさい。
ただし、さいころの目はどの目が出ることも同様に確からしいものとする。
ア 12未満になることの方が起こりやすい。
イ 12以上になることの方が起こりやすい。
ウ どちらも起こりやすさは同じ。
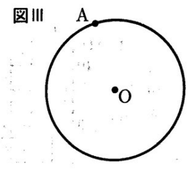
10 次の図Ⅲの円Oで、点が接点となるように、円Oの接線を作図しなさい。ただし、作図に用いた線は明確にして、消さずに残しておくこと。
解答
1（1） 【正答 -2】
1（2） 【正答 1/2】
1（3） 【正答 6√6】
1（4） 【正答 5x-y】
1（5） 【正答 3/2ab】
2 【正答 9x²-6xy+y²】
3 【正答 -3】
4 【正答 (x+6)(x-1)】
5 【正答 x=1】
6 【正答 x=1±√5/2】
7 【正答 27/4㎝】
8（1） 【正答 a=1/3】
8（2） 【正答 0≦ｙ≦16/3】
9 【正答 記号：ア
（理由）（例）積abが12以上となることの確率は1
+3+4+4+5/36=17/36
積abが12未満となることの確率は、
1-17/36=19/36>17/36
よって、アの12未満となることの方が起こりやすい。】
10 【正答】
大問2
問題文
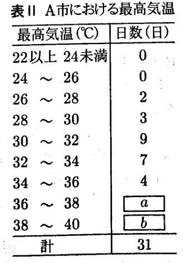
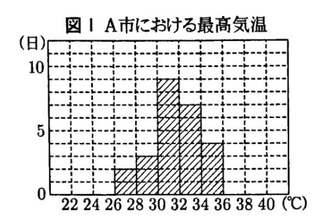
次の表Ⅰは、Ａ市とＢ市における、ある年の7月の各日の最高気温の記録である。あとの各問いに答えなさい。
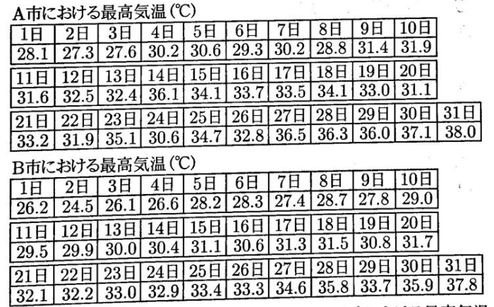
1 表Ⅱは、表ⅠのＡ市における最高気温の記録を度数分布表にまとめたものである。表Ⅱの【a】,【b】にあてはまる数を求め、図Ⅰのヒストグラムを完成させなさい。
2 次の表Ⅲ、図Ⅱは、表ⅠのＢ市における最高気温の記録を度数分布表とヒストグラムにまとめたものである。この表Ⅲまたは図Ⅱから最頻値を求めなさい。
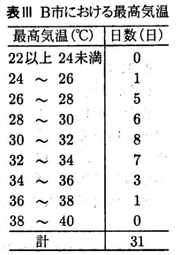
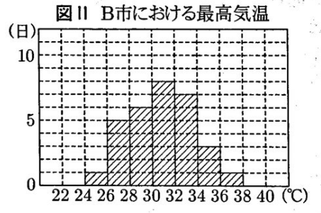
3 Ａ市とＢ市の度数分布表やヒストグラムからわかることとして、正しいものを、次のア～オからすべて選び、記号で答えなさい。
ア Ａ市は、26℃以上27℃未満の日が少なくとも1日ある。
イ Ａ市の度数が4である階級の階級値は、34℃である。
ウ Ａ市の中央値とＢ市の中央値を比べると、Ｂ市の方が低い。
エ Ｂ市の分布の範囲は14℃である。
オ Ｂ市の30℃以上32℃未満の階級の相対度数は0.25より大きい。
解答
1 【正答 a=5,b=1】
2 【正答 31℃】
3 【正答 ウ,オ】
大問3
問題文
右の図のような1辺の長さが3㎝の立方体がある。辺AB上に点Pを、辺AD上に点Qを、辺AE上に点RをそれぞれAP＝AQ＝AR=1㎝となるようにとる。
その3点P,Q,Rを通る平面で立方体を切断し、頂点Ａを含んだ立体を切り取る。
立方体の頂点Ｂ～Ｈに対しても、同様の操作を行う。
次の会話は、花子さんと太郎さんが、各頂点を切り取ったあと、残った立体の辺の数、頂点の数、面の数が、それぞれどうなるかについて話し合ったものである。
会話【ア】～【ケ】にあてはまる数を答えなさい。
会話
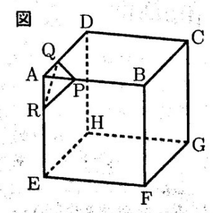
花子さん：「頂点Ａを含んだ立法を切り取る」という操作によって、残った立体の辺、頂点の面のそれぞれの数はどうなるのかな。
太郎さん：切り取る前の立方体の辺の数は【ア】本、頂点の数は【イ】個、面の数は【ウ】個だね。
花子さん：3点Ｐ，Ｑ，Ｒを通る平面で立法を切断した場合、立体ＡＰＱＲは三角錐になったね。残った立体の辺の数、頂点の数、面の数はどうなったかな。
太郎さん：残った立体の辺の数は【エ】本、頂点の数は【オ】個、面の数は【カ】個だよ。辺について考えてみると、切り取ることによって、新しくできた切り口に新たに辺ができているよ。
花子さん：確かにそうだね。では、これを参考にして「頂点を含んだ立体を切り取る」という操作を頂点B～Hに行い、同じように立体を切り取るとき、残った立体の辺の数、頂点の数。面の数が、それぞれどうなるのか考えてみようよ。
太郎さん：わかったよ。立方体のすべての頂点A～Hを同じように切り取るとき、残った立体の辺の数は【キ】本、頂点の数は【ク】個、面の数は【ケ】個だね。
解答
【正答
ア 12
イ 8
ウ 6
エ 15
オ 10
カ 7
キ 36
ク 24
ケ 14】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問4
問題文
ある中学校で、球技大会の日程を考えている。次の各問いに答えなさい。ただし、時間の単位は分とする。
1 次の図のように、試合時間をa分、チームの入れかわり時間をb分、昼休憩を40分をとる。
10試合を行うとき、最初の試合開始から最後の試合が終了するまでにかかる時間（分）を表す式を、aとbを用いて表しなさい。
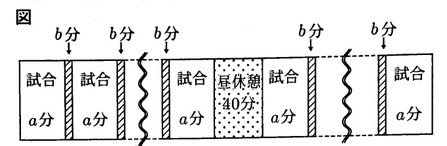
2 問1のとき、最初の試合を午前9時に開始して午後3時に最後の試合が終了するよう計画した。b=5のとき、試合時間（分）を求めなさい。
3 球技大会の種目をサッカーとソフトボールの2種目に決定し、次のように大会の計画をたてた。あとの（1）,（2）に答えなさい。
＜大会の計画＞
・サッカーの試合が、すべて終わった後に昼休憩を40分とり、その後ソフトボールの試合を行う。
・試合は午前9時に最初の試合を開始して、午後2時20分に最後の試合を終了する。
・サッカーは、4チームの総当たり戦で6試合行う。サッカー１試合の時間は、すべて同じ時間とする。
・ソフトボールは、5チームのトーナメント戦で4試合行う。ソフトボール１試合の時間は、すべて同じ時間とする。
・サッカーもソフトボールも１試合ずつ行い、試合と試合のあいだのチームの入れかわり時間は、4分とする。
・ソフトボール1試合の試合時間は、サッカー１試合の試合時間の1.6倍とする。
（1）この大会の計画にしたがって、サッカーとソフトボールの1試合の時間を決めることとした。サッカー1試合の時間をx分、ソフトボール1試合の時間をy分として連立方程式をつくりなさい。ただし、この問いの答えは、必ずしもつくった方程式を整理する必要はありません。
（2）サッカー1試合の時間（分）を求めなさい。
解答
1 【正答 10a+8b+40】
2 【正答 28分】
3（1） 【正答 （例）
ｙ＝1.6ｘ
6ｘ＋4ｙ＋8×4＋40＝320】
3（2） 【正答 20分】
大問5
問題文
右の図のように3点A,B,Cを通る円があり、△ABCは1辺の長さが9㎝の正方形である。BCは円周上の2点B,Cを両端とする弧のうち短い方を表すものとし、点PはBC上の点である。また、点を線分AP上にPC=PDとなるようにとる。このとき、次の各問いに答えなさい。
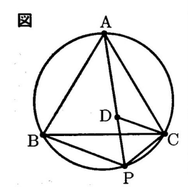
1 △ABCの面積を求めなさい。
2 △ADC△BPCであることを、次のように証明した。
証明の【1】,【2】にあてはまるものとして、最も適切なものを、あとの【1】,【2】の選択肢のア～エからそれぞれひとつずつ選び、記号で答えなさい。また、【3】にあてはまる三角形の合同条件を答え、この証明を完成させなさい。
ただし、証明の中にある【1】,【2】には、それぞれ同じ記号が入るものとする。
（証明）
△ADCと△BPCで
△ABCは正三角形だから AC＝BC…①
PCに対する円周角だから、∠PAC＝【1】
よって、∠DAC＝【1】…②
また、△ABCが正三角形だから ∠ABC＝60°
ACに対する円周角だから ∠ABC＝∠APC
よって ∠APC＝60°
これと、PC＝PDであることにより、△は正三角形である。よって、∠DCP＝60°
ここで、∠ACD＝60°-【2】
∠BCP＝60°-【2】
であるので、∠ACD＝∠BCP…③
①，②，③より【3】ので
△ADC△BPCである。
【1の選択肢】
ア ∠BAP
イ ∠PBC
ウ ∠CDP
エ ∠BCP
【2の選択肢】
ア ∠CDP
イ ∠APB
ウ ∠BAP
エ ∠BCD
3 AP＝10㎝のとき、四角形ABPCの周の長さを求めなさい。
4 線分BCと線分APの交点をQとする。BP：PC＝2：1のとき、△CDQの面積を求めなさい。
解答
1 【正答 81√3/4㎠】
2 【正答 1 イ，2 エ，3 1組の辺とその両端の角が、それぞれ等しい】
3 【正答 28㎝】
4 【正答 27√3/28㎠】
大問6
問題文
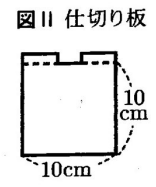
下の図Ⅰは、図Ⅱの仕切り板で9つに仕切られた容器である。次の図Ⅲのように、この容器のAの部屋に一定の割合で蛇口から水を入れ、Aの部屋の底面から水面までの高さが10㎝になった後、Aの部屋と隣り合っている部屋にそれぞれ同じ割合で水があふれていき、最終的にすべての部屋の水面が底面から10㎝の高さになったところで水を止める。Ａの部屋は、1分間で水面の高さが10㎝に到達した。ただし、この9つの部屋にはそれぞれ同じ体積の水が入り、各部屋の体積は1000㎤である。また、容器の壁や仕切り板の厚さは考えないものとする。
このとき、あとの各問いに答えなさい。
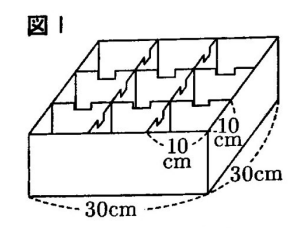
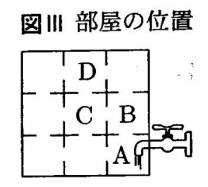
1 図ⅢのＡの部屋の水面の高さが10㎝になった後、Aの部屋からBの部屋には毎分何㎤の水が流れ込むか、求めなさい。
2 図ⅢのCの部屋の水面の高さが10㎝になるのは、Aの部屋に水を入れ始めてから何分後か、求めなさい。
3 図ⅢのDの部屋について、次の（1）,（2）に答えなさい。
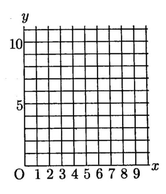
（1）Aの部屋に水を入れ始めてからx分後のDの部屋の水面の高さをy㎝とする。このとき、xとyの関係をグラフにかきなさい。ただし、xの変域は0≦x≦9とする。
（2）Ｄの部屋の水面の高さが8㎝となるのは、Aの部屋に水を入れ始めて何分後か、求めなさい。
解答
1 【正答 毎分500㎥】
2 【正答 5分後】
3（1） 【正答】
3（2） 【正答 38/5分後】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
