【山口県】令和3年度/2021年度入学者高校入試選抜試験：数学
山口県の2021年3月実施の令和3年度（2021年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の（1）～（5）に答えなさい。
（1） -7+9 を計算しなさい。
（2）15/2×(-4/5)を計算しなさい。
（3）10a -(6a + 8)を計算しなさい。
（4）27ab² + 9ab を計算しなさい。
（5）3(2x-y)+4(x+3y) を計算しなさい。
解答
（1） 【正答 2】
（2） 【正答 -6】
（3） 【正答 4a-8】
（4） 【正答 3b】
（5） 【正答 10x+9y】
大問2
問題文
次の（1）～（4）に答えなさい。
（1）次の【 】にあてはまる不等号を答えなさい。
小数第1位を四捨五入すると40になる数をxとする。このとき，xのとりうる値の範囲は，39.5≦x【 】40.5である。
（2）2つの整数m，nについて，計算の結果がいつも整数になるとは限らないものを，次のア～エから1つ選び，記号で答えなさい。
ア m+n
イ m-n
ウ m×n
エ m÷n
（3）yはxのに反比例し，x＝3のときy=2である。yをxの式で表しなさい。
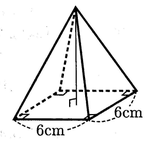
（4）底面が1辺6cmの正方形で，体積が96cm3である四角すいの高さを求めなさい。
解答
（1） 【正答 ＜】
（2） 【正答 エ】
（3） 【正答 y=6/x】
（4） 【正答 8㎝】
大問3
問題文
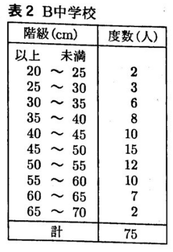
表1，表2は，それぞれA中学校の3年生全員25人とB中学校の3年生全員75人が行った長座体前屈の記録を度数分布表にまとめたものである。次の(1),(2)に答えなさい。
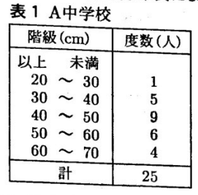
（1）表1をもとに，A中学校の3年生全員の記録の最頻値を，階級値で答えなさい。
（2）A中学校とB中学校の3年生全員の記録を比較するために，階級の幅をA中学校の10cmにそろえ，表3のように度数分布表を整理した。記録が60cm以上70cm未満の生徒の割合は，どちらの中学校の方が大きいか。60cm以上70cm未満の階級の相対度数の値を明らかにして説明しなさい。
解答
（1） 【正答 45㎝】
（2） 【正答 （例）60cm以上70cm未満の階級cmの相対度数は，A中学校が4/25=16/100=0.16，B中学校が9/75=3/25=12=100=0.12なので，A中学校の方が求める生徒の割合は大きいといえる。】
大問4
問題文
確率について，次の(1)～(3)に答えなさい。
（1）あたる確率が2/7 であるくじを1回引くときあたらない確率を求めなさい。
（2）1枚の硬貨があり，その硬貨を投げたとき表が出る確率と裏が出る確率はいずれも1/2である。この硬貨を多数回くり返し投げて，表が出る回数をa 回裏が出る回数をb回とするとき次のア～工の説明のうち，正しいものを2つ選び，記号で答えなさい。
ア 投げる回数を増やしていくと，a/bの値は1/2に近づいていく。
イ 投げる回数を増やしていくと，a/a+bの値は1/2に近づいていく。
ウ 投げる回数が何回でも，aの値が投げる回数と等しくなる確率は0ではない。
エ 投げる回数が偶数回のとき，bの値は必ず投げる回数の半分になる。
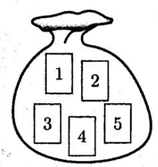
（3）図のような，数字1, 2, 3, 4, 5が1つずつ書かれた5枚のカードが入った袋がある。袋の中のカードをよく混ぜ．同時に3枚取り出すとき取り出し た3枚のカードに書かれた数の和が3の倍数となる確率を求めなさい。
解答
（1） 【正答 5/7】
（2） 【正答 イ，ウ】
（3） 【正答 2/5】
大問5
問題文
平方根や二次方程式について，次の（1）～（3）に答えなさい。
（1）14の平方根のうち，正の数であるものを答えなさい。
（2）次の【 】にあてはまる数を求めなさい。
二次方程式x²-2x+a=0の解の1つが1+√5であるとき，a=【 】である。
（3）差が1である大小2つの正の数がある。これらの積が3であるとき，2つの数のうち，大きい方を求めなさい。
解答
（1） 【正答 √14】
（2） 【正答 -4】
（3） 【正答 1+√13/2】
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問6
問題文
関数y=ax²について，次の(1)～(3)に答えなさい。
（1）次の【 】にあてはまる数を答えなさい。
関数y=5x²のグラフと，x軸について対称なグラフとなる関数はy=【 】x²である。
（2）関数y=-3/4x²について，次のア～エの説明のうち，正しいものを2つ選び記号で答えなさい。
ア 変化の割合は一定ではない。
イ xの値がどのように変化しても，yの値が増加することはない。
ウ xがどのような値でも，yの値は負の数である。
エ グラフの開き方は，関数y=-x²のグラフより大きい。
（3）図のように，2つの放物線①，②があり．放物線①は関数y=-1/2x²のグラフである。また，放物線①上にある点Aのx座標は4であり，直線AOと放物線②の交点Bのx座標はー3である。このとき放物線②をグラ フとする関数の式を求めなさい。
解答
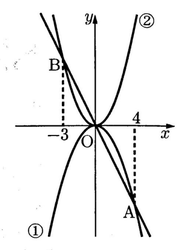
（1） 【正答 -4】
（2） 【正答 ア，エ】
（3） 【正答 y=2/3x²】
大問7
問題文
図1のような， 点Oを中心とする半径4の円Oと，図2のような，点 O’を中心とする半径の円O’がある。 次の（1）～（3）に答えなさい。
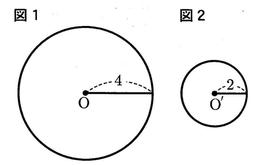
（1）次の【 】にあてはまる数を求めなさい。
円Oと円O’の面積比は，【 】：1である。
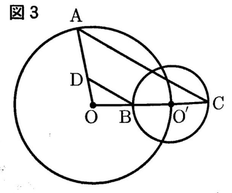
（2）図3において，2点O’，Aは円Oの周上にあり，2点B，Cは直線CO’と円Oの交点である。線分OA上に，AC//DBとなるような点Dをとったとき，線分ADの長さを求めなさい。
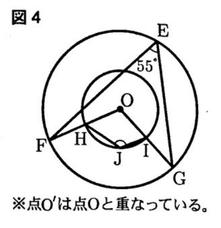
（3）図4において，点Oと点O’は同じ位置にあり， 3点E，F，Gは円Oの周上にある。また，2点H，Iは，それぞれ線分OF，OGと円O’の交点であり．点Jは弧HI上にある。∠GEF= 55°であるとき，∠HJIの大きさを求めなさい。
解答
（1） 【正答 4】
（2） 【正答 8/3】
（3） 【正答 125度】
大問8
問題文
一次関数について，次の(1)，(2)に答えなさい。
（1）表は，yがXの一次関数であり，変化の割合が-3であるときのxとyの値の関係を表したものである。表中の【 】にあてはまる数を求めなさい。
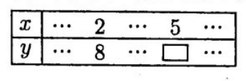
（2）図のように，2つの一次関数y= -x+a，y=2x+bのグラフがあり，X軸との交 点をそれぞれP,Qとし，y軸との交点をそれぞれR，Sとする。次の説明は， PQ= 12，RS=9のときの，aとbの値を求める方法の 1 つを示したものである。
説明中の【 】にあてはまる，aとbの関係を表す等式を求めなさい。また，a,bの値をそれぞれ求めなさい。
説明
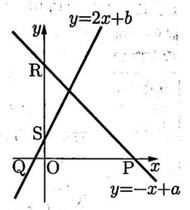
PQ= 12より，
【 】…①
RS=9より，
a-b=9…②
①，②を連立方程式として解くと，a,bの値を求めることができる。
解答
（1） 【正答 -1】
（2） 【正答 式：a+b/2=12，a=11，b=2】
大問9
問題文
図形の回転移動について，次の(1),(2)に答えなさい。
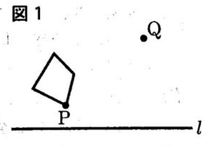
（1）図1において，点Pを頂点に もつ四角形を，点Oを回転の中心として，点Pが点Qの位置に移るように回転移動させる。点Oが直線ｌ上にあるとき，点Oを定規とコンパスを使って作図しなさい。ただし，作図に用いた線は消さないこと。
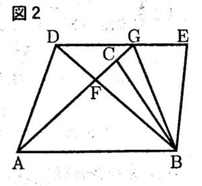
（2）図2において，△DBEは△ABCを，点Bを回転の中心として， DE//AB となるように回転移動したものである。線分ACと線分BDの交点をF，線分ACの延長と線分DEの交点をGとするとき，△FDA≡△FGBであることを証明しなさい。
解答
（1） 【正答 】
（2） 【正答 （例）
△FDAと△FGBにおいて，
仮定より△DBE≡△ABCなので，
∠BDE=∠BAC…①
AB//DEなので，平行線の錯角より，
∠BDE=∠ABD…②
∠BAC=∠DGA…③
①，②より，∠FAB＝∠FBAとなり，△FABは2つの角が等しいことから，二等辺三角形となり，FA=FB…④
①，③より，∠FDG＝∠FGDとなり，△FDGは2つの角が等しいことから，二等辺三角形となり，FD=FG…⑤
また，対頂角は等しいので，∠DFA＝∠GFB…⑥
④，⑤，⑥より，2組の辺とその間の角がそれぞれ等しい ので，△FDA≡△FGB】
大問10
問題文
Yさんのクラスでは文化祭で，集めた空き缶を並ぺて大きな長方形の絵にする空き缶アートをつくることになった。
Yさんは，空き缶アートの大きさや，並べる空き缶の個数を確認するため，図1のように，空き缶を底面が直径6.6㎝の円で高さが12.2cmの円柱として考えることにした。また，2個の空き缶を縦に並べると，図2のように0.3㎝重なった部分ができた。
この空き缶を図3のように並べて空き缶アートにし，正面から見たものを長方形ABCDと表す。
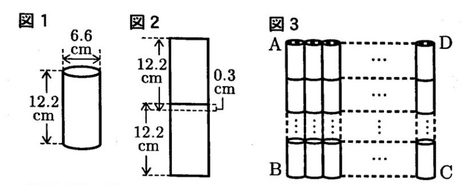
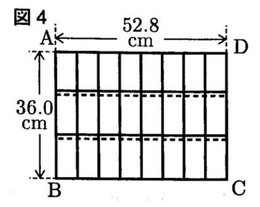
例えば，図4のように， 縦に3 個， 横に8 個の空き缶を並べると，並べる空き缶の個数の合計は24個であり，長方形ABCDの縦の長さABは36.0 cm，横の長さADは52.8cmとなる。
次の(1)～(3)に答えなさい。
（1）縦に20個の空き缶を並べるとき，横に並べる空き缶の個数に比例しないものを， 次のア～エから1つ選び，記号で答えなさい。
ア 並べる空き缶の個数の合計
イ 長方形ABCDの横の長さ
ウ 長方形ABCDの4辺の長さの合計
工 長方形ABCDの面積
（2）横に105個の空き缶を並べ，横の長さADが縦の長さ ABより300cm長い空き缶アー トをつくる。このとき縦に並べる空き缶の個数を x 個として一次方程式をつくり，縦に並べる空き缶の個数を求めなさい。ただし，答えを求めるまでの過程も書きなさい。
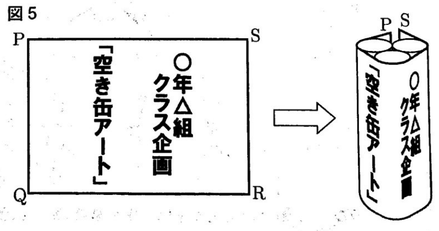
（3）Yさんは，余った空き缶と，文字を書いた長方形の用紙を使い，案内板をつくることにした。
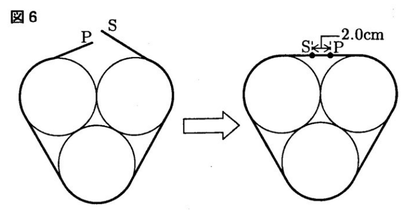
図5のように長方形の用紙PQ郎を，3個の空き缶 が互いに接するように並べて縦に重ねたものに巻きつける。線分PQが空き缶の底面に垂直になるように巻きつけると，用紙の左右の端が2.0cm重なった。図6は，巻きつける様子を真上から見たものである。
このとき，図5の長方形の用紙PQ郎の横の長さPSを求めなさい。ただし，円周率はπとする。
解答
（1） 【正答 ウ】
（2） 【正答 （例）横に105個の空き缶を並べるので， 横の長さADは， AD=6.6×105=693(cm)
1縦に空き缶をx個並べると考えると，縦の長さABは，
AB=12.2+11.9×(x-1)=11.9x+0.3(cm)
したがって，
11.9x+0.3+300=693
となるので，これを解いて，ｘ＝33
（答え） 33個】
（3） 【正答 (6.6π+21.8)cm】
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
