【山口県】令和4年度/2022年度入学者高校入試選抜試験：数学
山口県の2022年3月実施の令和4年度（2022年度）入学者の公立高校入試問題の解説をしています。
受験勉強において、過去問を解くことはとても効果的な勉強法です。ぜひ、受験までに一度挑戦し、問題の傾向を掴んでおきましょう。合わせて、対策などをたてられるととても良いですね。
また、過去問で苦手な点が見つかった場合は、そこを中心に試験日当日までにしっかりと対策しておきましょう。
大問1
問題文
次の（1）～（5）に答えなさい。
（1） 8-（-5） を計算しなさい。
（2）2/5÷（-1/10）を計算しなさい。
（3）（-4a）²×3b を計算しなさい。
（4）（6x+y）-（9x+7y） を計算しなさい。
（5）（a+3）（a-3）を計算しなさい。
解答
【解答】
（1） 【正答 13】
（2） 【正答 -4】
（3） 【正答 48a²b】
（4） 【正答 -3x-6y】
（5） 【正答 a²-9】
【解説】
（1） 8-（-5）＝8+5＝13
（2） 2/5÷（-1/10）＝-2/5×10＝-4
（3） （-4a）²×3b＝16a²×3b＝48a²b
（4） （6x+y）-（9x+7y）＝6x+y-9x-7y＝-3x-6y
（5） （a+3）（a-3）＝a²-9
大問2
問題文
次の（1）～（4）に答えなさい。
（1） 直方体の形をした水槽があり、水槽の底から7ｃｍの高さまで水が入っている。この水槽に、毎分3ｃｍずつ水面が上がるように水を入れる。水を入れ始めてからｘ分後の水槽の底から水面までの高さをｙcmとしたとき、水槽が満水になるまでのｘとｙの関係について、ｙをｘの式で表しなさい。ただし、ｘの変域はかかなくてもよい。
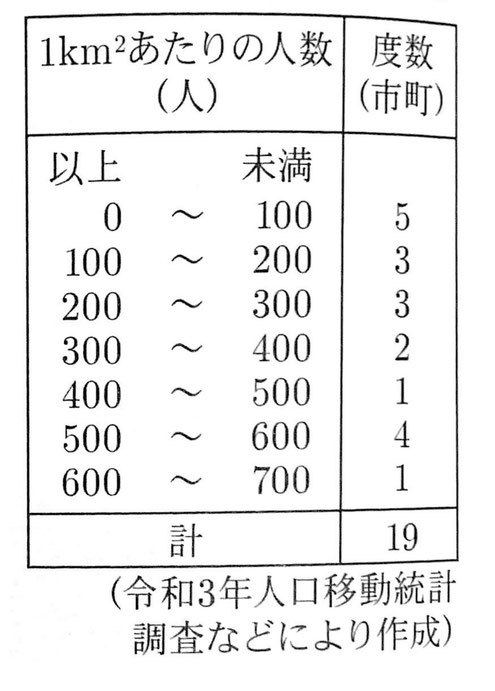
（2） 次の表は、山口県の19市町別の人口密度（1km²あたりの人数）を度数分布表にまとめたものである。
19市町の中央値が含まれている階級を、次のア～エから1つ選び、記号で答えなさい。
ア 100人以上200人未満
イ 200人以上300人未満
ウ 300人以上400人未満
エ 400人以上500人未満
（3） 次の条件①と条件②の両方を満たす数を答えなさい。
条件① 4より大きく5より小さい無理数である
条件② 2乗すると18より小さい整数となる
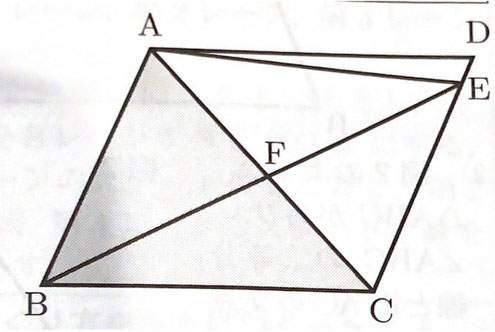
（4） 次の図のような平行四辺形ABCDで、辺CD上にあり、頂点C,Dと重ならない点をE,線分ACと線分DEの交点をFとする。
このとき、△ABCと面積の等しい三角形を、次のア～エから1つ選び、記号で答えなさい。
ア △ACE
イ △BCE
ウ △ABE
エ △BCF
解答
【解答】
（1） 【正答 y=3x+7】
（2） 【正答 イ】
（3） 【正答 √17】
（4） 【正答 ウ】
【解説】
（1） はじめに水面の高さが7cmあり、そこから毎分3cmずつ水面が上がっていくので、変化の割合は3である。
（2） 中央値は人口密度の低い方から10番目となるので、中央値の属する階級は、200人以上300人未満。
（3） 求める数をnとすると、条件①より、√16＜n＜√25、この中で条件②n²＜18を満たすのは、n=√17のみ。
（4） AB//CDより、△ABCと△ABEは共に底辺をABとすると、その高さも等しいことから面積も等しくなる。
大問3
問題文
SさんとTさんは、インターネットを利用する機会が増えたので、データ量や通信料に興味をもった。次の（1）、（2）に答えなさい。
（1） Sさんのタブレット端末には、1枚3MBの静止画がa枚、1本80MBの動画がb本保存されており、それらのデータ量の合計は500MBよりも小さかった。この数量の関係を不等式で表しなさい。なお、MBとは、情報の量を表す単位である。
（2） SさんとTさんはそれぞれ、アプリケーションソフトウェア（以下、「アプリ」）PとQを使用したときの、インターネット通信料を調べた。下の表はその結果である。アプリP,Qはどちらも、使用時間と通信料が比例することが分かっている。
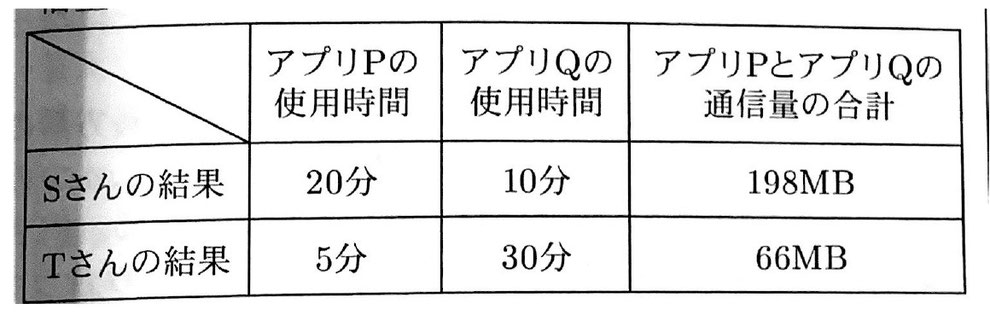
このとき、アプリPの1分間当たりの通信料をxMB、アプリQの1分間あたりの通信料をyMBとして連立方程式を作り、アプリP,Qの1分間あたりの通信料をそれぞれ求めなさい。なお、MBとは、情報の量を表す単位である。
解答
【解答】
（1） 【正答 3a+80b＜500】
（2） 【正答 式：20x+10y=198、5x+30y=66 アプリP：9.6MB アプリQ：0.6MB】
大問4
問題文
空間図形について、次の（1）、（2）に答えなさい。
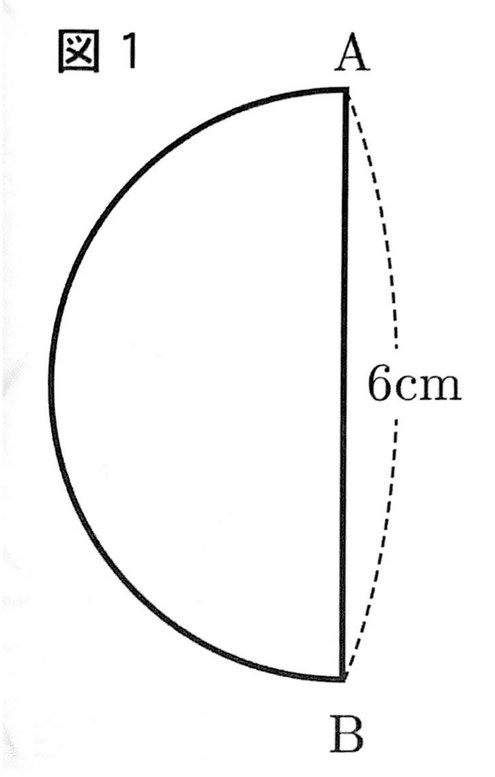
（1） 図1のような直径ABが6cmの半円がある。線分ABを軸としてこの半円を1回転してできる立体の体積を求めなさい。ただし、円周率はπとする。
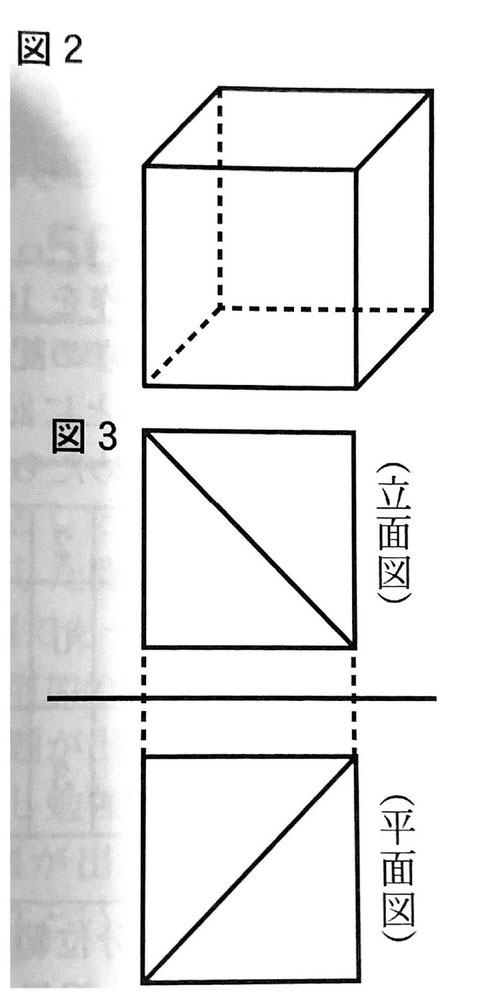
（2） 図2は1辺の長さが1ｍである立方体である。この立方体を、ある3つの頂点を通る平面で切り取ると、立体Ｘと立体Ｙができる。図3は立体Ｘの投影図である。
立体Ｘの体積をＶ、立体Ｙの体積をＶ’としたとき、体積の比Ｖ：Ｖ’を、次のア～エから1つ選び、記号で答えなさい。
ア Ｖ：Ｖ’＝1：1
イ Ｖ：Ｖ’＝3：1
ウ Ｖ：Ｖ’＝5：1
エ Ｖ：Ｖ’＝7：1
解答
【解答】
（1） 【正答 36πcm³】
（2） 【正答 ウ】
【解説】
（1） 半径3ｃｍなので、4π×3³/3＝36π（cm³）
（2） 立体Ｙの体積Ｖ’＝1×1×1/2×1×1/3＝1/6（ｍ³）、立体Ｘの体積Ｖ＝1－Ｖ’＝5/6（ｍ³）
0120-740-100
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
大問5
問題文
AさんとBさんは花壇に花の苗を植える計画を立てた。次の（1）（2）に答えなさい。
（1） 買ってきた花の苗を5人で植えると、1人あたり70個変えることになる。買ってきた花の苗をa人で植えると、1人あたり何個植えることになるか。aを使った式で表しなさい。
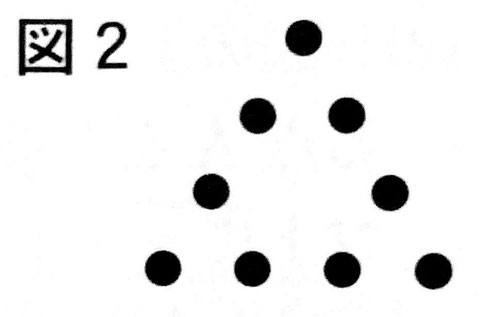
（2） AさんとBさんは、買ってきた花の苗の一部を使って図1のように、花の苗を三角形の辺上に同じ数ずつ植えることにした。例えば、花の苗を三角形の辺上に4個ずつ植えると、図2のようになる。ただし、●は花の苗を表す。
Aさんは、三角形の辺上にn個ずつ植えるときの、苗の合計を次のように考えた。
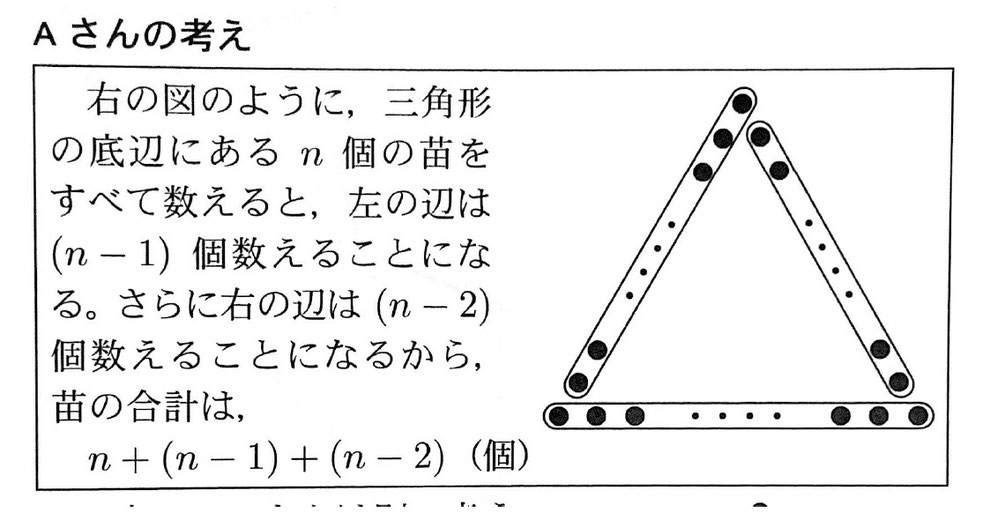
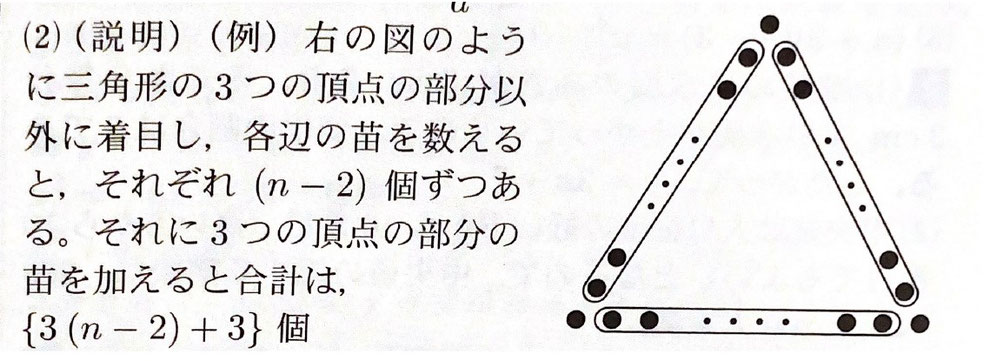
一方で、Bさんは別の考え方で、｛3（n-2）+3｝個と考えた。Bさんの考え方について、Aさんの考え方に習って、●を囲んだうえで説明しなさい。
解答
【解答】
（1） 【正答 350/a個】
（2） 【正答 下図参照】
大問6
問題文
大小2個のさいころについて、次の操作を行うとき、次の（1）、（2）に答えなさい。ただし、この大小2個のさいころは、どの目が出ることも同様に確からしいものとする。
操作
大小2個のさいころを同時に1回投げて、出た目の数の和を記録する。
（1）下の表は、操作を10回繰り返したときの記録Aと50回繰り返したときの記録Bを整理したものである。また、説明は、表をもとに記録Aと記録Bの散らばり度合いについてまとめたものである。
| 目の数の和 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 10回くりかえしたときの記録A | 0 | ||||||||||
| 50回くりかえしたときの記録B |
説明
記録Aの四分位範囲は（ア）、記録Bの四分位範囲は5である。記録Aと記録Bの四分位範囲を比較すると、記録（イ）の方が散らばりの度合いが大きい。
説明 が正しいものとなるように、（ア）には、あてはまる数を求め、（イ）には、A、Bのうち適切な記号を答えなさい。
（2） 操作を多数回繰り返していくと、目の数の和が6，7，8になる回数が他よりも多くなっていくことが分かっている。大小2個のさいころを同時に1回投げたとき、目の数の和が6以上8以下になる確率を求めなさい。ただし、答えを求めるまでの過程も書きなさい。
解答
【解答】
（1） 【正答 ア：3 イ：B】
（2） 【正答 下記参照】
（例）大小2個のさいころを投げたときの出る目は全部で36通りある。そのうち、和が6以上8以下になる目の出方は
（大、小）＝（1，5）（1，6）（2，4）（2，5）（2，6）（3，3）（3，4）（3，5）（4，2）（4，3）（4，4）（5，1）（5，2）（5，3）（6，1）（6，2）の16通りなので、求める確率は16/36＝4/9
【解説】
（1） 記録Aは、第1四分位数が6、第3四分位数が9なので、四分位範囲は9-6＝3、記録Bの四分位範囲は5なので、四分位範囲が大きい方がデータの散らばりが大きいといえる。
大問7
問題文
関数y=ax²について、次の（1）（2）に答えなさい。
（1） 関数y=x²について、xの値が1から2まで増加したときの変化の割合は3である。xの値が-3から-1まで増加したときの変化の割合を求めなさい。
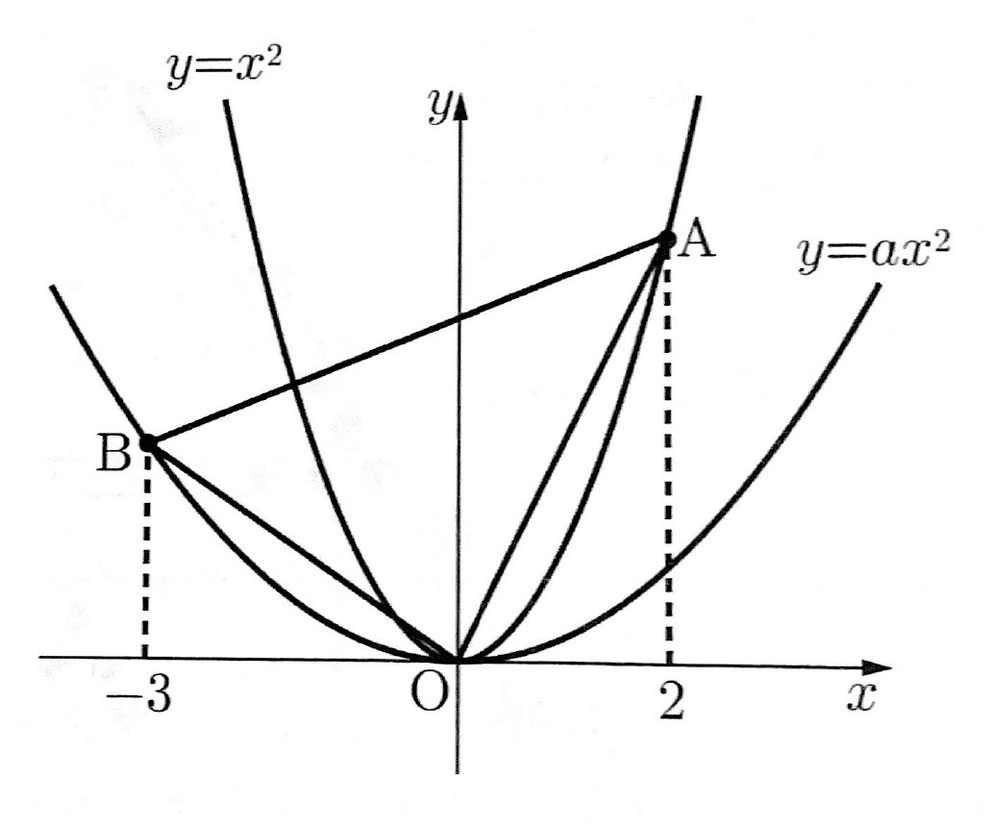
（2） 図のように、関数y=x²のグラフ上にx座標が2となる点Aをとる。またa>0である関数y=ax²のグラフ上にx座標が-3となる点Bをとる。△OABの面積が8となるとき、aの値を求めなさい。
解答
【解答】
（1） 【正答 -4】
（2） 【正答 a=2/9】
【解説】
（1） ｘ＝-3のときｙ＝9、ｘ＝-1のときｙ＝1なので、変化の割合は1-9/-1-（-3）＝-4
（2） 直線ABとｙ軸との交点をＤとする。△OABの面積が8となるとき、OD×｛2-（-3）｝×1/2＝8、OD＝16/5となり、D（0,16/5）となる。よって、2点A,Dの座標から直線ABの傾きは、（4-16/5）÷（2-0）＝2/5とわかるので、直線ABの式はy=2/5x+16/5、これにB（-3,9a）を代入すると、a=2/9
大問8
問題文
三角形に関連して、次の（1）（2）に答えなさい。
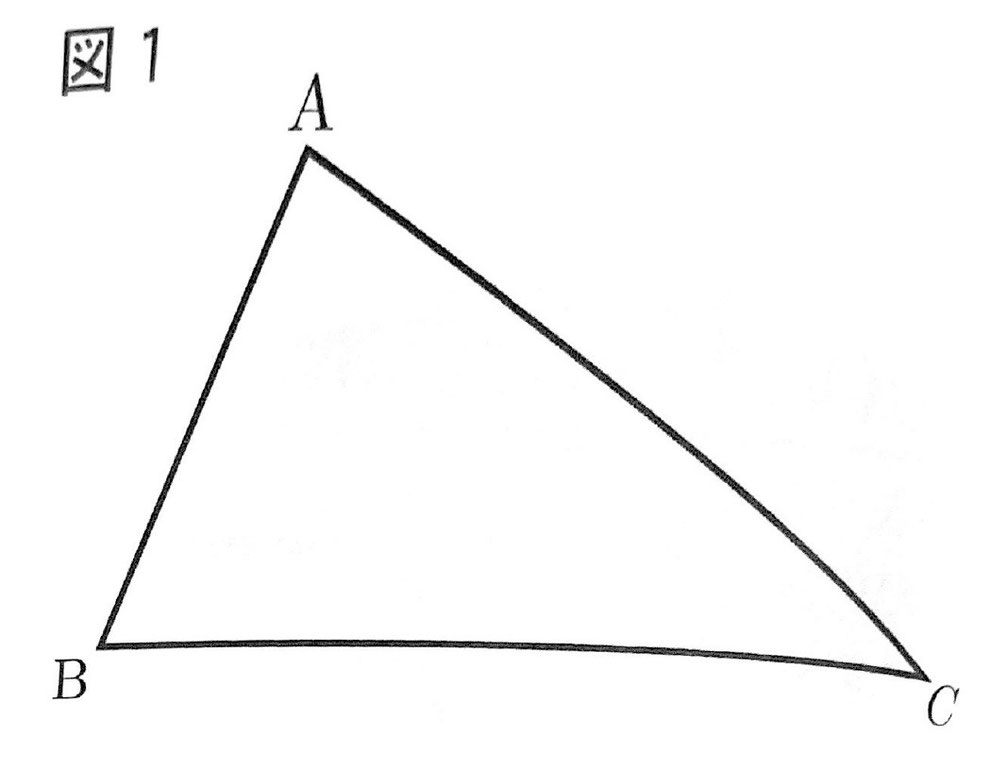
（1） 図1のように、∠ABC＝70°、∠ACB＝30°である△ABCがある。辺AC上に点D、辺BC上に点Eをとり、∠BDE＝55°、∠BED＝90°であるような直角三角形BEDをつくりたい。このとき、点Eを定規とコンパスを使って作図しなさい。ただし、作図に用いた線は消さないこと。
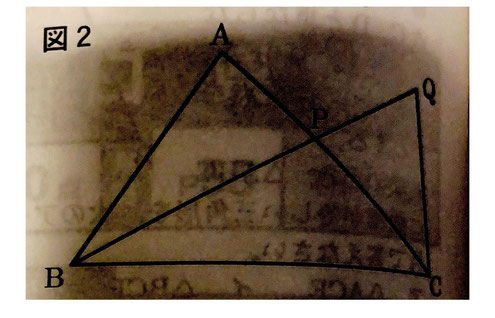
（2） 図2のような△があり、∠ABCの二等分線と辺ACの交点をPとする。また、線分BPの延長上にあり、CP＝CQとなる点Qをとる。
このとき、BA:BC＝AP:CPであることを証明しなさい。
解答
【解答】
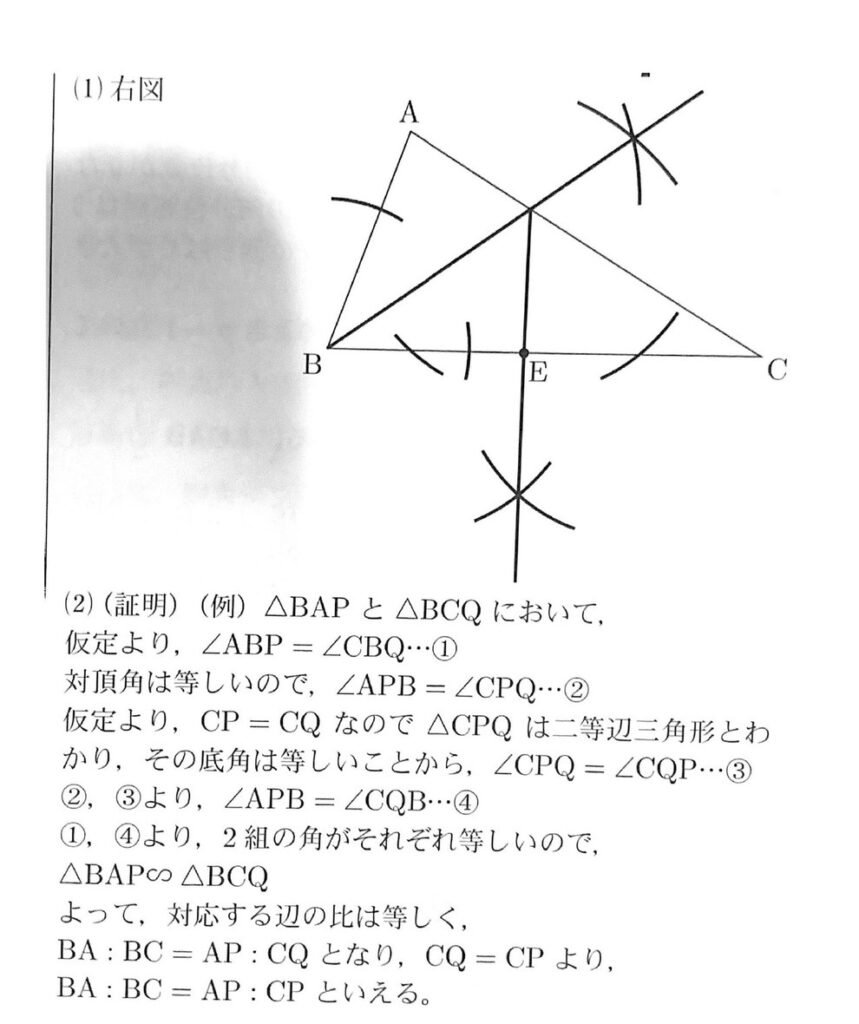
（1） 【正答 下図参照】
（2） 【正答 下記参照】
大問9
問題文
ある中学校では、体育祭の準備を行っている。次の（1）～（3）に答えなさい。
（1） Sさんは、倉庫にある玉入れ用の玉の中に、使える玉が何個かあるか確認することにした。そこで、無作為に抽出した20個の玉を調べると、そのうち15個が使える玉であった。
玉が全部で413個あることが分かっているとき、使える玉はおよそ何個と推定されるか。小数第1位を四捨五入した概数で答えなさい。
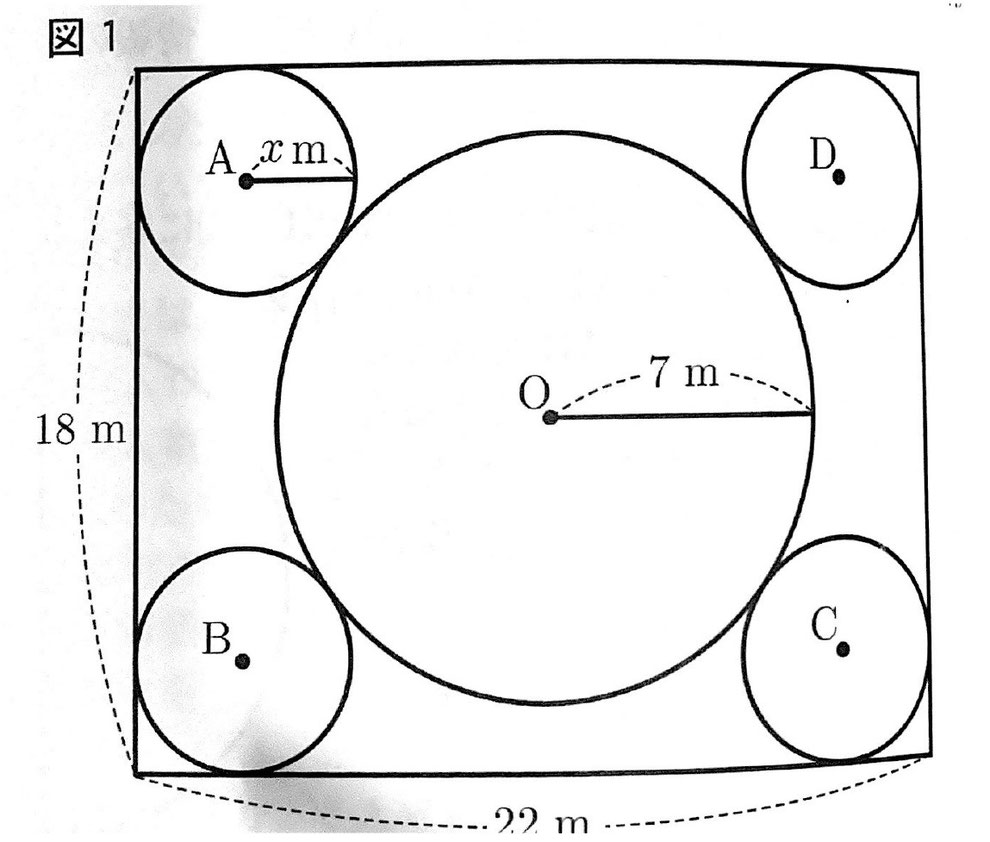
（2） Tさんのクラスでは、ダンスの隊形について話し合っている。ダンスは運動場に用意された縦18ｍ、横22ｍの長方形の形をした区域の中で踊ることになっている。
図1は、Tさんが考えた隊形を示しており、長方形の対角線の交点を中心とした半径7ｍの円Ｏと、4つの同じ大きさの円A,B,C,Dを表したものである。円A,B,C,Dは、円Oより小さく、長方形の隣り合う2辺と円Oに接している。
円A,B,C,Dの半径をxｍとしたとき、xの値を求めなさい。
（3） Uさんは、運動場に200ｍ走のトラックをつくることになった。そこで、陸上競技用のトラックの作り方について調べ、以下のように作るようにした。
トラックの作り方
① 半径がrｍの2つの半円と、縦の長さが2rｍ、横の長さがbｍの長方形を組み合わせる。
② ①の図形の外側に、幅が1ｍの4つのレーンをつくり、内側から第1レーン、第2レーン、第3レーン、第4レーンとする。
③ 各レーンのゴール位置は同じライン上とし、トラックを走る距離を各レーンすべて200ｍにする。そのため、第1レーンのスタート位置に対し、第2レーン、第3レーン、第4レーンのスタート位置をそれぞれ前方にずらす。
図2はトラックの作り方をもとに つくったイメージ図である。第1レーン、第4レーンのスタート位置の最も内側の点を、それぞれA,Bとする。①の2つの半円のうち、ゴール位置のある方の半円の中心を点Cとする。
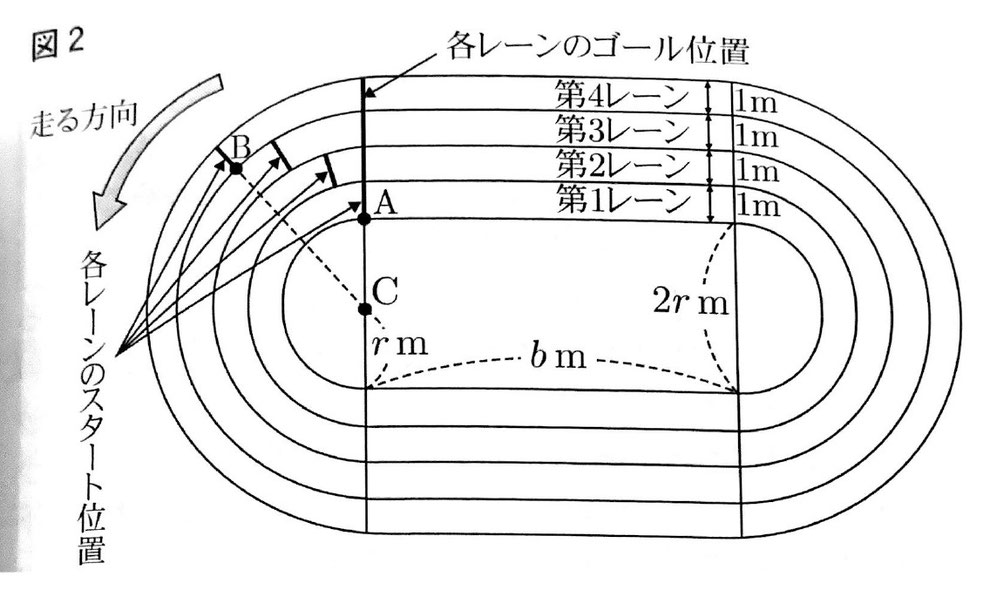
実際にトラックを作るために、Uさんは図2を使ってクラスメイトに下のように説明した。この説明が正しいものとなるように（ア）、（イ）にあてはまる数を求めなさい。また（ア）については、答えを求めるまでの過程も書きなさい。ただし、円周率はπとする。
各レーンで走る距離は、各レーンの内側にある線の長さを測るものとする。第4レーンのスタート位置は、第1レーンのスタート位置より（ア）ｍだけ前方にずらす必要がある。r=21としてつくると、∠ACBの大きさは（イ）度となる。
解答
【解答】
（1） 【正答 およそ310個】
（2） 【正答 ｘ＝3】
（3） 【正答 ア：下記参照 イ：45度】
【解説】
（1） 413×15/20＝1239/4＝309.7…となり、およそ310個。
（2） 直角三角形ABCをつくり三平方の定理を利用する。AB＝18-2ｘ、BC＝22-2ｘ、AC＝14+2ｘより、（14+2ｘ）²＝（18-2ｘ）²+（22-2ｘ）²、ｘ＜7より、ｘ＝3
（3）ア 第1レーンの1周のながさは（2πr+2b）ｍであり、第4レーンの1周の長さは｛（2r+6）π+2b｝ｍとなる。その距離の差は｛（2r+6）π+2b｝-（2πr+2b）＝6π（ｍ）より、第4レーンの方が6πｍだけ長いので、走る距離を同じにするためには、第4レーンのスタート位置は第1レーンのスタート位置より6πｍだけ前方にずらす必要がある。
（3）イ r=21なら、第4レーンの曲線部分の半円の半径が24で、半円の弧の長さは24π。このうち6πだけスタート位置が前にいくので、∠ACB＝180°×6/24＝45°
志望校に合わせた受験対策なら、やる気アシストにお任せ下さい！
家庭教師のやる気アシストでは、毎年スタッフが関西エリア各府県の入試問題を分析し、例年の傾向や次年度に向けての対策を行っています！
教育の現場は時代に合わせて目まぐるしく変化していくため、毎年対策を考えていく必要があります。「家庭教師って塾に比べて受験対策とかしっかりしてくれるの…？」とご質問いただくことも多いですが、ご安心ください！家庭教師だからこそ、お子さんの志望校、志望校の傾向など個々に合わせてより細やかなサポートをすることができるんです！
受験指導について気になることやわからないことがあればまずはアシストまでご連絡ください。専門スタッフがお子さんの受験勉強についてご相談に乗らせていただきます！
LINE問合せ窓口
LINEからもお問合せいただけます！
公式Instagram
勉強のお役立ち情報を配信中！
お問い合わせ、ご質問も受付中です！
ご質問などお気軽にお問い合わせください。
アシストの指導方法がじっくり見れる！知れる！無料の体験授業実施中
お子さんにとって「成果が出る勉強法」ってどんな勉強法だと思いますか？
お子さんそれぞれに、個性や性格、学力の差もあります。そんな十人十色のお子さん全員に合う勉強法ってなかなかないんです。
たからこそ、受験生の今だけでもお子さんだけの勉強法で受験を乗り越えてみませんか？
やる気アシストには、決まったカリキュラムはありません。お子さんの希望や学力、得意や不得意に合わせて、お子さんだけのカリキュラムで指導を行っていきます。また、勉強法もお子さんそれぞれに合う合わないがあります。無料体験授業では、お子さんの性格や生活スタイルを見せていただき、お子さんにとって効率的な成果の出る勉強のやり方をご提案させて頂きます。
