理科の中でも電気の分野は考える事が多く、計算量も多い為、困っているお子さんが多いと思います。
その中でも、「オームの法則」は特に頭を悩ませる内容の一つです。

今回はこのオームの法則とは何か、そしてこれを用いた「電圧」「電流」「抵抗」の求め方について解説していきます！

オームの法則について

そもそもオームの法則とは？

そもそもオームの法則とは何かというと、
「電流を流れにくくする部分(抵抗)での、電流・電圧・抵抗の関係を表した法則」
のことです。

オームの法則を式で表すと？

オームの法則を式で表すと、

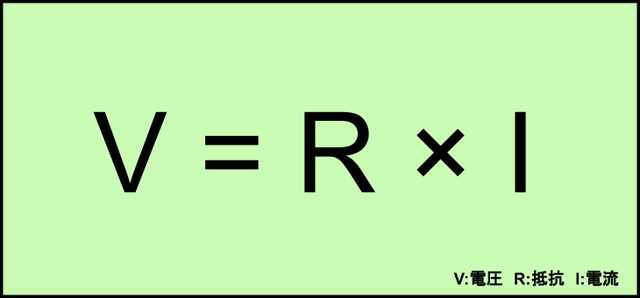
となります。ここで、
Vは電圧、Rは抵抗、Iは電流です。

回路中の電圧・電流・抵抗を求める方法は？

オームの法則によって、回路中に流れる電圧・電流・抵抗を決めることができます。
まず、電圧と抵抗が分かっている場合に電流を求めることができます。
例えば

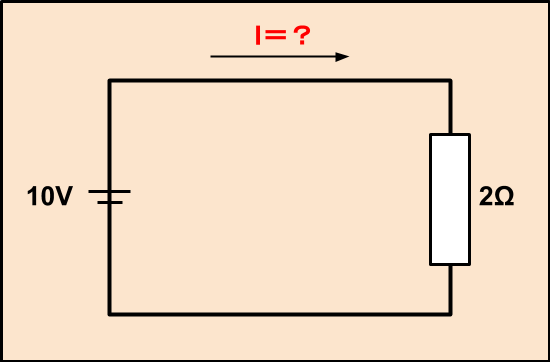
のような回路があったとします。
電圧が10V、抵抗が2Ωの時の電流はオームの法則を用いて計算することができ、
10=2×I
I=5
より、電流は5Aと分かります。

また、電流と電圧が分かっている場合の抵抗を求めることができます。

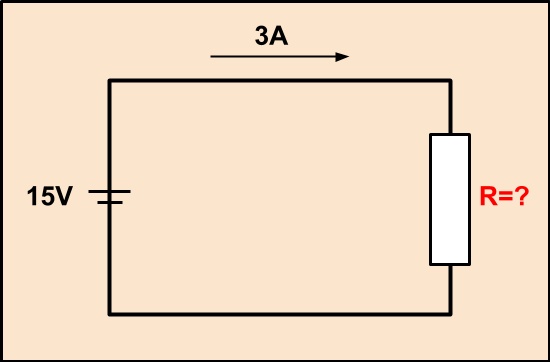
のように、電流が3A、電圧が15Vと分かるとき、抵抗はオームの法則より、
15=R×3
R=5
となり、抵抗は5Ωであると分かります。

最後に、電流、抵抗が分かっているときの電流を求めることができます。

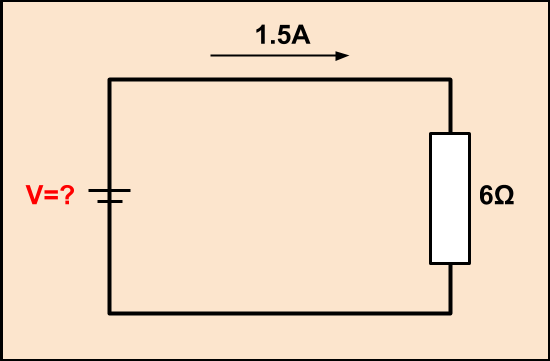
のように、電流が1.5A、抵抗が6Ωと分かるとき、電圧はオームの法則より、
V=1.5×6=9
となり、電圧は9Vであると分かります。

このように、電圧、電流、抵抗のうち、2つが分かれば、のこり1つを知ることができます。

抵抗が同じ時の電圧と電流の関係は？

抵抗が同じ時、電圧と電流の関係はどのようになっているのか考えてみましょう。
例えば、抵抗が10Ωのとき、電流を1Aずつ増やしていくと、電圧がどのように増えていくか計算してグラフに表してみると、

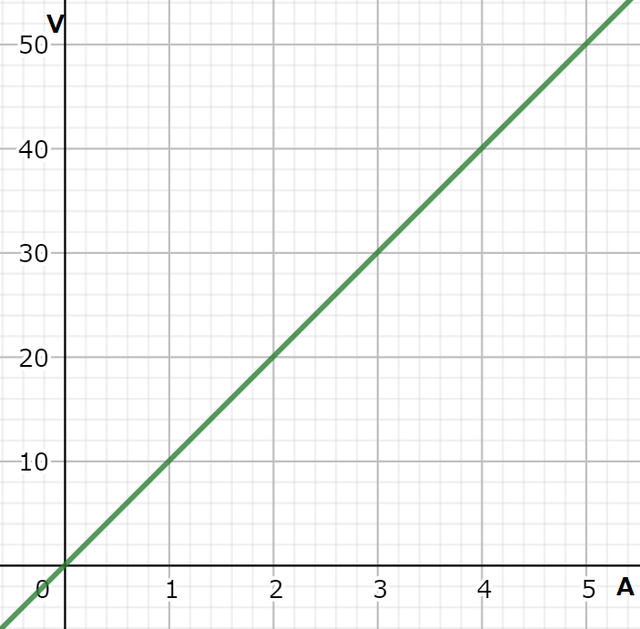
のようになります。
抵抗が同じ時は、電圧と電流が比例の関係となります。

また、同様に抵抗が5Ωのときを考えて、10Ωの場合と重ねると、

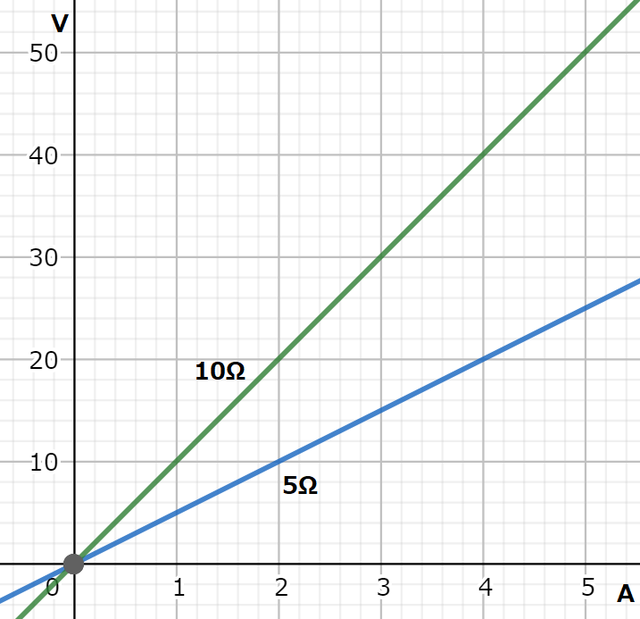
のようになります。
グラフより、電圧が10Vの時の電流を見てみると、10Ωの時は1A、5Ωの時は2Aであると分かります。

また、電流が1Aの時の電圧を見てみると、10Ωの時は10V、5Ωの時は5Vであると分かります。
このことから、
• 抵抗が大きいほど、ある電圧の時に電流が流れにくい
• 抵抗が大きいほど、ある電流を流すための電圧が大きくなる
ということが分かります。

テストの時に、式だけを覚えて臨むと、当日急に忘れてしまって困ることもあるので、
上の2つのように、意味を理解しておくとより確実だと思います！

水の流れで考えると分かりやすい

電気の流れは水の流れで考えると非常にわかりやすいです！
電圧・電流・抵抗を水路に例えると、
• 電圧は「水の位置(高さ)」
• 電流は「時間当たりに流れる水の量」
• 抵抗は「水の流れを妨げるもの」
とすることができます。

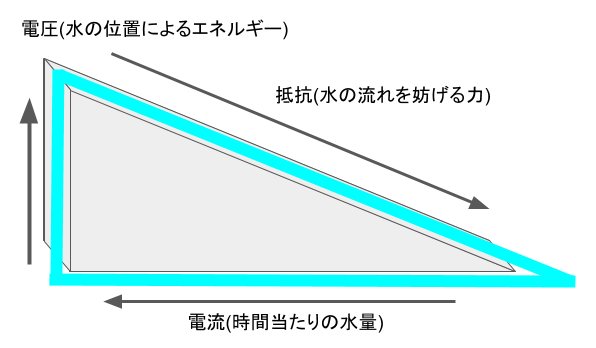
抗は水路でいうと、高さを下げる部分になるので、現時点で勉強する回路には必ず抵抗が必要です。(抵抗が無いと「ショート」という危険な現象が発生してしまいます。)

＼小・中・高校生の勉強にお悩みのある方へ／

2つ以上の抵抗を含む場合は？

抵抗は回路中にいくつでも入れることができます。
ここで難しいのが「直列」につないだ場合と「並列」につないだ場合の計算が違う点です。

抵抗が直列の場合

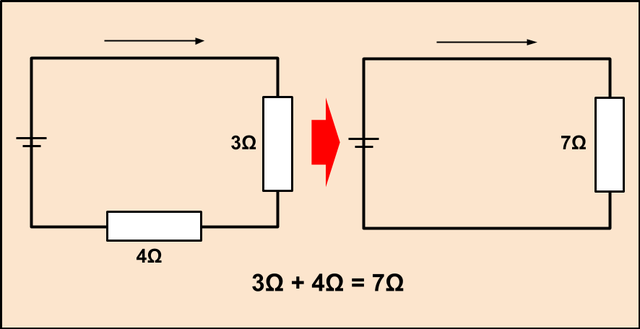
上の図のように、抵抗が直列に2つついている場合は、
二つの抵抗の値を合計して、\一つの抵抗として扱うことができます。
この場合、3Ωの抵抗と4Ωの抵抗が直列につながっているので、これらを計算して、
7Ωとなります。
3つの抵抗を直列につなぐ場合も、2つの場合と同様にどんどん足し合わせていけばOKです。

抵抗が並行の場合

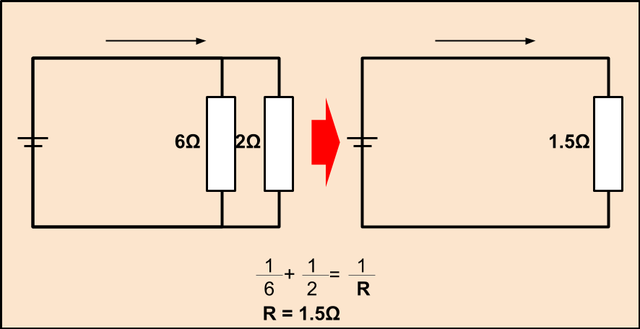
上の図のように、抵抗が並列に2つついている場合は、
分数の足し算によって2つの抵抗を1つの抵抗としてみなすことができます。

この場合、6Ωと2Ωの抵抗が並列についているので、図の下にあるように式をつくると、
この抵抗は1.5Ωとみなすことができると分かります。
抵抗が3つ以上の場合も同様に分数の数を増やして計算することができますよ。