エネルギーという言葉を聞いたことがあっても、これがどういったものなのか説明することができる人はあまりいないと思います。
今回は、エネルギーってなんなのか、そして、物体にはどんなエネルギーが掛かっているのかについて、身近な例を含めて説明していきます。
定期テストや宿題でつまづいてしまっている方は、是非読んでみて下さいね!
力の向きを変えたり、変形させる力をもつ物体を「エネルギーがある」物体といいます。エネルギーが大きいほど、力の向きを変えたり、変形させたりする能力をもつということです。
物体がもつエネルギーには「運動エネルギー」と「位置エネルギー」の2種類があります。
運動エネルギーとは「動くことができるエネルギー」、位置エネルギーは「場所によるエネルギー」という風に言えます。これらのエネルギーは実際の世の中で視ることはできませんが、常に存在しているものです。
運動エネルギーは、物体の質量が重く、速度が大きいほど大きくなるエネルギーです。
具体的には、物体の質量に比例し、速度の2乗に比例して大きくなります。
物同士がぶつかるとき、より早く、より重いほど、変形したり破壊されたりするというのは想像に難しくはないですよね。
位置エネルギーは、物体が基準の高さよりも高い位置にあるほど大きくなるエネルギーです。50cmの高さから落ちたときと、2mの高さから落ちたときでは、当然2mの高さから落ちる方が痛いことは分かると思います。
また、球を物の下に落とすと、高いところから落とすほど強い勢いで当たることも想像に難くないと思います。
このように、高さが違うだけで、その物体がもつエネルギーが変わるのです。動いていなくても持っているエネルギーというところが運動エネルギーとの違いですね。
力学的エネルギーとは、運動エネルギーと位置エネルギーの合計のことを表します。
この力学エネルギーは、外から力を受けない限り、一定となります。
なので、もし物体の運動エネルギーが減ったとき、その減った分を丁度埋めるだけ位置エネルギーが増えるということになります。
では、その具体的な例を挙げてみましょう。
まず振り子を想像してみてください。昔ながらの時計についているあれです。
この振り子が力学的エネルギーを説明するのが一番簡単な例になります。
一番左端をスタート、一番右端をゴールとしましょう。(順番はどちらでも大丈夫です)
スタート地点では振り子は動いていませんが、エネルギーはたくさん持っています。
上で説明した通り、動いていなくても持っているエネルギー:位置エネルギーを持っていますね。
運動エネルギーは動いていないのでゼロです。
ではこの運動エネルギーが一番大きくなる、速度が速くなる時はどんな時でしょうか?
答えは一番下に行ったときです。
この時は位置エネルギーはゼロです。
さて最後にゴール地点を見てみましょう。
振り子は動いていないので運動エネルギーはゼロになります。
代わりに一番高いところにいるので位置エネルギーは最大になるということが分かりますね。
このような、位置エネルギーと運動エネルギーの和が一定に保たれることを、
力学的エネルギーの保存
といいます。
グラフ位置エネルギーと運動エネルギーの関係を図で表してみると、
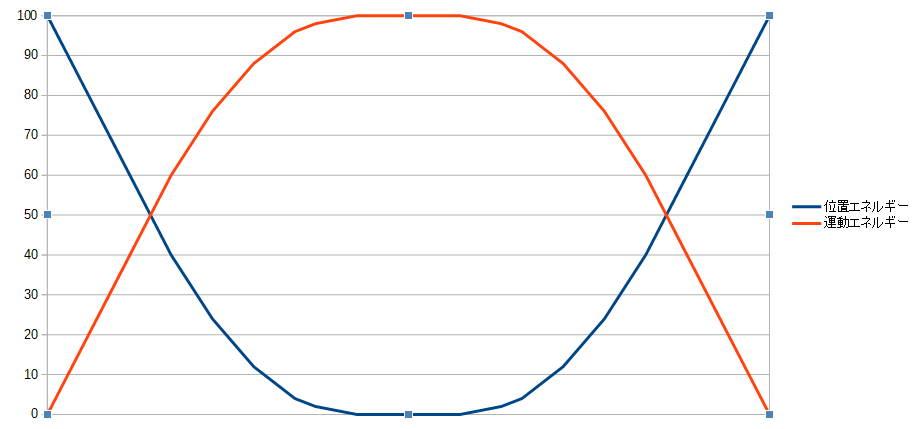
のようになります。力学的エネルギーが100あるとして、どの地点にあっても、位置エネルギーと運動エネルギーの和が100に保たれています。
\小・中・高校生の勉強にお悩みのある方へ/
力学的エネルギーの考え方は現実で実際に応用されています。
その最たる例が、ジェットコースターです!
ジェットコースターは一番最初に、最も高い点に向けてカタカタと上っていきます。このときは、リフトの力によって上に押し上げているので、力学的エネルギーは保存されていません。
さて、リフトの力が掛からなくなり、ジェットコースターの最高点に達します。ここから先は、基本的に進むための力を他から受けることなく滑るように落ちたりまた上ったりすることができます。これは運動エネルギーと位置エネルギーの考えが使われているんですね。
ところで、ジェットコースターは一番最初が最高点で、それ以降はそれを超えることがありません。
なぜかというと、最初の位置が「位置エネルギー最大、運動エネルギー0」という、さっきの斜面を転がる球のような状態なので、それより上にいくためのエネルギーが無いからです。
(摩擦力・空気抵抗が掛かっているので、厳密には力学的エネルギーの保存はされていません。)