前回は、正の数・負の数について学びました。

今回は足し算と引き算のやり方を学んでいきます。本文中でも触れますが、数直線をイメージすると理解がしやすいです。
ただ、数が大きくなった時の為に他のやり方もご紹介していきますので参考にしてください。
次回の掛け算を読んでから再度読んでみると理解が深まると思います。

それでは早速やっていきましょう！

1.同符号どうしの足し算

最初に言葉の説明から始めたいと思います。
タイトルにある「加法」。これは足し算のことです。また、足し算によって得られた答えのことを「和」と呼びます。

正の数と正の数の加法は今までやってきたものと変わらないので、ここでは負の数と負の数の加法をピックアップして解説していきます。

1-1.数直線のイメージで理解しよう

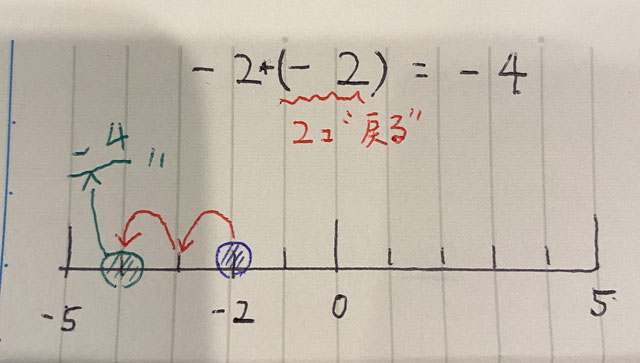
数直線で確認してみましょう。
－２は数直線で考えると2つ”戻る”と考えることができます。
現在「－２」に居るところから２つ戻ると「－４」のところに移動するので、答えは－４と分かります。

1-2.同符号は数字をそのまま計算

数が小さいときは、上のような数直線のイメージで問題ないと思いますが、数が増えてきた場合はどうでしょうか？
例えば－２５＋（－５４）のような式があったとき、数直線を書いて54こ戻って・・・等はややこしいですよね。

そこで同符号の時は、符号をそのままにして数字のみ足し算すると覚えておくと対応できます。

今回の場合、符号は「－」でそのまま。数字の部分は25+54＝79。よって答えは－79である。といった次第です。

2.異符号どうしの足し算

次に異符号どうしの足し算について解説していきます。
今回も、数直線を使う方法とそれ以外の方法の２パターンから見ていきます。

2-1.数直線のイメージで理解しよう

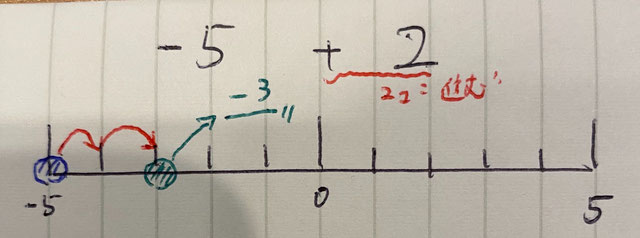
負の数+正の数のケースを見てみましょう。
＋２は数直線で考えると2つ”進む”と考えることができます。

現在「－５」に居るところから２つ進むと「－３」のところに移動するので、答えは－３と分かります。

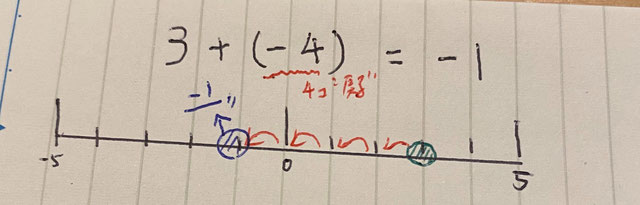
次は、正の数+負の数のケースを見てみましょう。
－４は数直線で考えると4つ”戻る”と考えることができます。
現在「＋３」に居るところから4つ戻ると「－１」のところに移動するので、答えは－１と分かります。

2-2.異符号は絶対値を利用して解く

それでは数字が大きくなった時に対応できるように、他のやり方も学んでおきましょう。
異符号の時は、符号を絶対値の大きい数字の方に揃えて数字を引き算すると対応することができます。

加法なのに引き算！？と混乱するといけないので実際の問題で確認してみましょう。

例題2

以下の式を計算せよ。
（1）－45＋32
（2）58+（－46）

解説2

（1）は負の数の方が絶対値が大きいので、符号は「－」にします。
そして数字部分は引き算をすればよいので４５－３２＝１３となるので
答えは－１３になります。

（2）は正の数の方が絶対値が大きいので、符号は「＋」にします。
そして数字部分は引き算をすればよいので５８－４６＝１２となるので
答えは＋１２になります。

＼小・中・高校生の勉強にお悩みのある方へ／

3.正負の数の引き算

それでは今回の肝となってくる引き算について学んでいきましょう。
少し複雑ですが、最初にお伝えした通り掛け算を学んでから見てみると凄く簡単に理解が出来るようになります。

まずは言葉の確認からやっていきます。
タイトルにある「減法」。これは引き算のことです。また、引き算によって得られた答えのことを「差」と呼びます。

①正の数と正の数
②正の数と負の数
③負の数と正の数
④負の数と負の数
のうち、①は今まで通りなので省略します。②～④を数直線の方法で解いていきたいと思います。

3-1.数直線のイメージで理解しよう

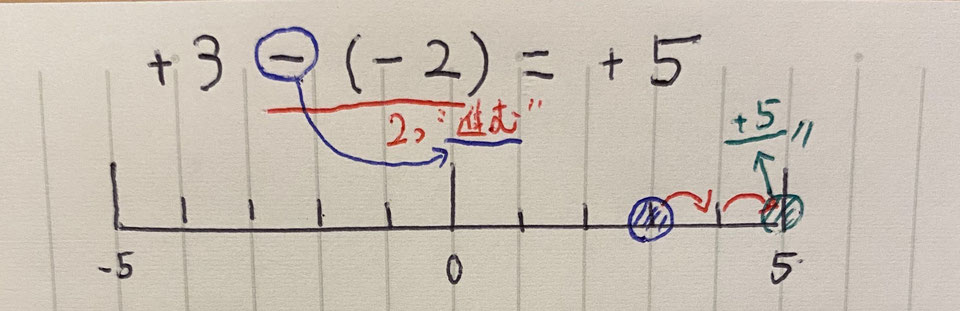
②のケースです。
引き算の時は”進む”と”戻る”が逆になります。
つまり、－２はこの時2つ”進む”と考えることができます。
現在「＋３」に居るところから2つ進むと「＋５」のところに移動するので、答えは＋５と分かります。

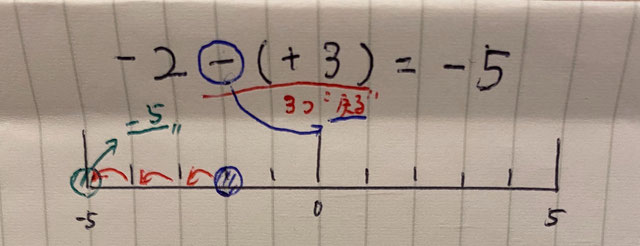
③のケースです。
引き算の時は”進む”と”戻る”が逆になります。
つまり、＋３はこの時3つ”戻る”と考えることができます。
現在「－２」に居るところから3つ戻ると「－５」のところに移動するので、答えは－５と分かります。

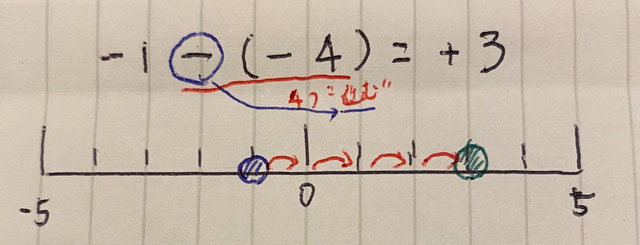
④のケースです。
引き算の時は”進む”と”戻る”が逆になります。
つまり、－４はこの時4つ”進む”と考えることができます。
現在「－１」に居るところから4つ進むと「＋３」のところに移動するので、答えは＋３と分かります。

3-2.掛け算を少し予習しよう

コラム的な内容です。
詳しくは次回解説をしていきますが、正負の数の掛け算の性質として
同符号どうしは符号が「＋」に、異符号どうしは符号が「－」になるという性質があります。

これを元に、②～④を見ていくと
②＋３－（－２）＝＋３＋２＝＋５
③－２－（＋３）＝－２－３＝－５
④－１－（－４）＝－１＋４＝＋３
となります。えっ？っとなった方は次回の記事でしっかり解説していきます！！