【数学】比例のグラフの書き方と特徴

前回は比例とは何だろうかということについて学んでいきました。

今回は前回勉強した内容を元に、座標の読み取り方から、比例のグラフの書き方、比例のグラフの特徴までまとめていきます。
グラフの書き方はテストでよく出てくるのでしっかり押さえていきましょう！

1.座標とグラフ

さて、それでは座標の基本的な言葉から学んでいきましょう。
点を表すための「座標」は、横軸のｘ座標と縦軸のｙ座標からなります。

横軸のことをｘ軸、縦軸のことをｙ軸と呼びます。
ｘ軸とｙ軸の交わる点を原点と呼び、原点の座標は（0,0）で表します。
座標の表し方は（ｘ座標の値，ｙ座標の値）で書き表します。

例題1

次の点ア～カの座標を答えよ。

解説1

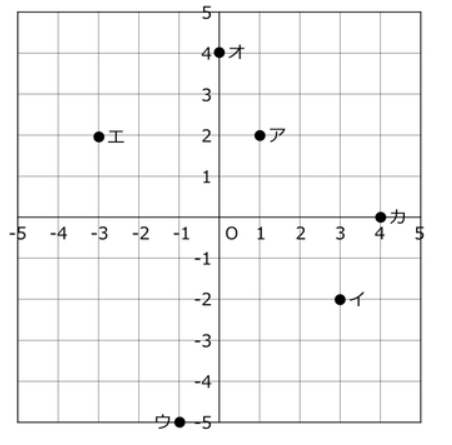
座標の表し方は（ｘ座標の値，ｙ座標の値）で書き表します。
ア（1,2）イ（3、-2）ウ（-1,5）エ（-3,2）オ（0,4）カ（4,0）
オやカのように軸上にある点は0を用いて表します。

＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／

家庭教師のやる気アシストなら最短0日で家庭教師を体験！無料の体験授業を実施中です！

＼小・中・高校生の勉強にお悩みのある方へ／

2.比例のグラフの書き方

この章ではグラフの書き方について学んでいきたいと思います。今回は比例のグラフですが、ここで学ぶやり方は直線のグラフを書くときに応用できるのでしっかり押さえていきましょう！

関数のグラフは、ある式を満たす点の集合です。
比例の関係であれば、比例の式を満たすｘとｙの値を、ｘ座標とｙ座標として、座標上に点をとっていくことで、グラフを書くことができます。
つまり、直線の通る2点が分かれば、グラフが書けるということです！

特に比例のグラフは、原点を通る直線になり、傾きは「y=ax」のaで決まります。
つまり、原点を必ず通ることから、傾きを考えるとグラフは2点が分からなくてもグラフを書くことができます。

ここで傾きを復習してみましょう。前回解説しましたが、傾きは変化の割合と同じ意味で、「yの増加量／ｘの増加量」と同じことになります。
グラフで考えると「縦に進む数／横に進む数」で表せるということになります。

例えばｙ＝2/5ｘという式があった時、通る点を求めなくとも、原点からスタートし、縦に2つ、横に5つ進んだ場所を通っていくということが分かります。
実際に問題を解いて感覚を掴んでいきましょう！

例題2

次の①～④のグラフの式を表せ。

解説2

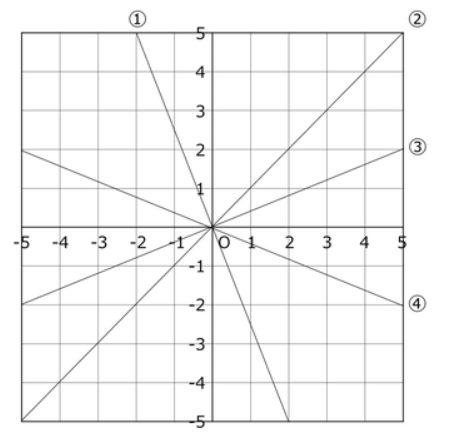
①通る点を見ると（-2,5）を通っています。原点から横に2つ戻り、縦に5つ進んでいるので傾きは「5/（-2）」となります。
よって、ｙ＝-5/2ｘが答えになります。

②通る点を見ると（1,1）を通っています。原点から横に1つ進み、縦に1つ進んでいるので傾きは「1/1」となります。
よって、ｙ＝ｘが答えになります。

③通る点を見ると（5,2）を通っています。原点から横に5つ進み、縦に2つ進んでいるので傾きは「2/5」となります。
よって、ｙ＝2/5ｘが答えになります。

④通る点を見ると（5,-2）を通っています。原点から横に5つ進み、縦に2つ戻っているので傾きは「-2/5」となります。
よって、ｙ＝-2/5ｘが答えになります。

＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／