






前回は平面図形について学んでいきました。
今回は空間図形の分野に入り、基本の言葉を中心に学んでいきましょう!
中学校1年生の数学の中で最大の山ですが、ここを越えれば後はちょろっとした計算の分野だけなので頑張って押さえていきましょう。
それでは立体の構造を持つ、空間図形について学んでいきたいと思います。
今までは「縦の長さ」と「横の長さ」だけでしたが、新しい尺度として「高さ」が加わります。
有名な形の名称から学んでいきたいと思います。

一番メジャーな空間図形はこの形だと思います。見ての通りサイコロです。
この図形の名称は「立方体」と呼びます。詳しくはこの後学びますが「正六面体」という呼び方もあります。
特徴としては全ての面が正方形で形作られているという特徴があります。
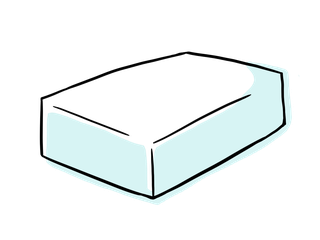
次にこの形を見てみましょう。上の立方体と比べて面の形が違いますね。
この図形の名称は「直方体」と呼びます。
特徴としては全ての面が長方形または、正方形で形作られているという特徴があります。

最後にこの図形です。三角形が垂直に引っ張られたような形になっています。
この図形の名称は「三角柱」と呼びます。
特徴としては三角形と長方形または正方形で形作られているという特徴があります。
前項で触れた立方体のように、全ての面が同じ正多角形で作られた多面体を正多面体と呼びます。
正多面体は全部で5つしかありません。それぞれの特徴を表にまとめていきたいと思います。
| 立体名 | 正四面体 | 正六面体 | 正八面体 | 正十二面体 | 正二十面体 |
|---|---|---|---|---|---|
| 面の形 | 正三角形 | 正方形 | 正三角形 | 正五角形 | 正三角形 |
| 頂点の数 | 4 | 8 | 6 | 20 | 12 |
| 面の数 | 4 | 6 | 8 | 12 | 20 |
| 辺の数 | 6 | 12 | 12 | 30 | 30 |
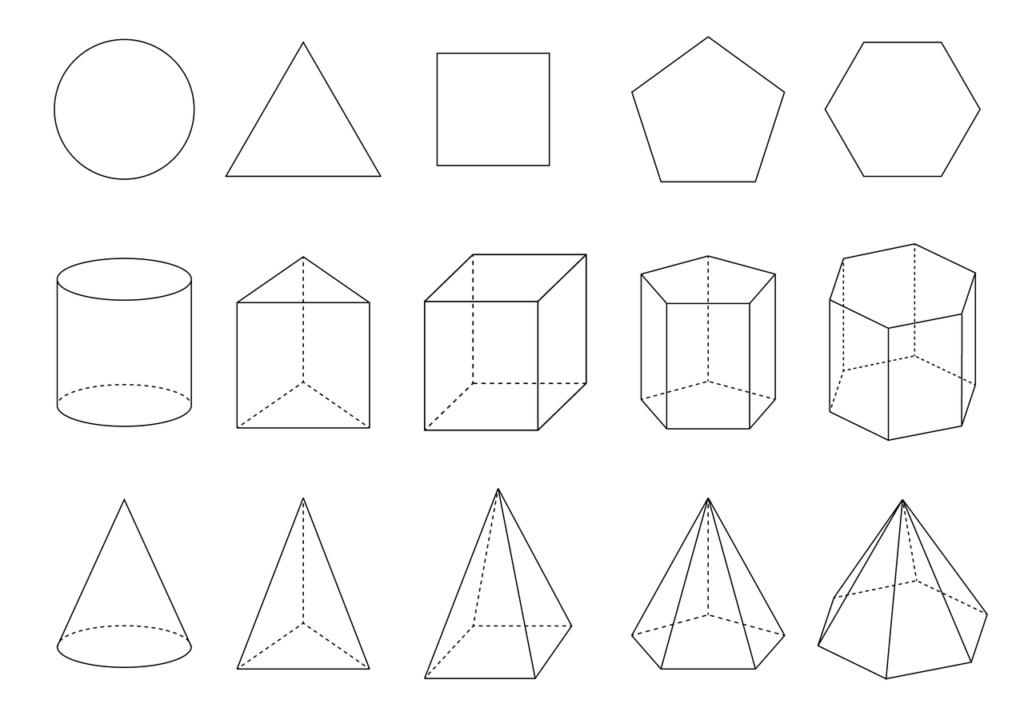
上の画像の一番上の行、左から順番に図形の名称の確認をしてみましょう。
それぞれ”円、三角形、四角形、五角形、六角形”でしたね。
縦の列で見ていくと同じ形の部分があると思います。この共通する部分、正確には空間図形上や下にある面のことを「底面」と呼びます。また、横の部分の面を「側面」と呼びますので合わせて覚えておきましょう。
次に二番目の行と三番目の行の違いを見ていきましょう。
二番目の行は底面が2つあることが分かりますね。このような形のことを「柱」と呼びます。
三番目の行は底面が1つだけで先端が尖っていることが分かります。このような形のことを「錐」と呼びます。
最後に立体の名前の付け方を見ていきましょう。
例として三番目の行の四列目を見てみます。確認項目は二つ。①底面の形②柱か錐か、です。
①底面の形は五角形です。
②底面が1つで先端が尖っているので錐になります。
よって、この図形は「五角錐」というのが図形の名前になります。
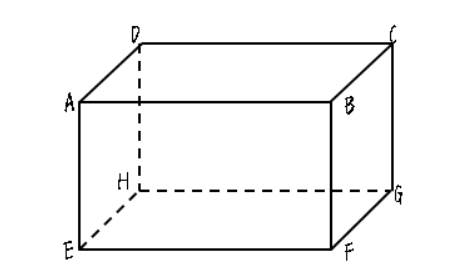
上図のような直方体の平行・垂直、ねじれの位置について学んでいきたいと思います。
特にねじれの位置は今回初めて登場する語句なので、しっかり押さえていきましょう。
まず面ABCDに注目しましょう。
この面に平行な面は向かいにある面EFGHが平行な面になります。
垂直な面は4つあり、面ABFE・面BCGF・面CDHG・面DAEHが垂直な面になります。
次に辺ABに注目しましょう。
この辺に平行な辺は3つあり、辺DC・辺EF・辺HGが平行な辺になります。
垂直な辺は4つあり、辺AE・辺AD・辺BF・辺BCが垂直な辺になります。
最後にねじれの位置について学んでいきたいと思います。
ねじれの位置とは平行でなく、交わることがない直線のことです。
直方体の場合は消去法で考えればよく、平行でも垂直でもない場合がねじれの位置となります。
すなわち、辺ABのねじれの位置になる辺は、辺DH・辺CG・辺EH・辺FGになります。
ここの分野がまさに想像力を使う分野です。実際の問題を見ながらが理解しやすいので例題を見てみましょう。
(1)正三角形を垂直な方向に動かすとどのような立体が出来るか答えよ。
(2)円を垂直な方向に動かすとどのような立体が出来るかを答えよ。
(3)長方形をその一辺を軸に回転させるとどのような立体が出来るかを答えよ。
(4)直角三角形を直角をつくる辺を軸に回転させるとどのような立体が出来るかを答えよ。
(1)第一章の第一項目にあるように、答えから書くと、「正三角柱」になります。
垂直な移動をするときは底面がその形の「柱」になることに注目します。
つまり、底面は正三角形なので正三角柱が正解となります。
(2)(1)と同様に考えましょう。
底面は円であり、垂直移動で「柱」になるので、「円柱」が答えになります。
(3)(4)の解説をするまえに回転させる移動の場合どうなるかを学んでいきましょう。
1つの直線を軸として、平面図形を回転させて出来る立体を「回転体」と呼びます。回転体の底面は必ず円になることが特徴です。
以上を踏まえて考えていきましょう。
(3)回転移動なので底面は必ず円になりましたね。ここで「柱」になるのか「錐」になるのかが大切です。
長方形は回転体になったときに底面を2つもつことになるので、「円柱」が答えになります。
(4)逆に直角三角形の時は、回転体になった際に底面が1つだけなので、「円錐」が答えになります。
\小・中・高校生の勉強にお悩みのある方へ/
立体(正確には立体の見取り図)を切り開いて平面で表した図形のことを「展開図」と呼びます。
また、少し触れた「側面」の面積のことを「側面積」と呼びます。
ここからは代表的な3つの立体の展開図と側面積を学んでいきたいと思います。
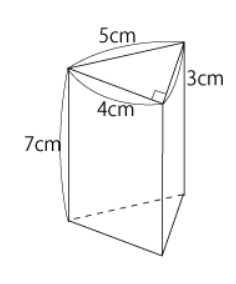
左図のような三角柱を切り開いて展開図にしてみると、下図のような形になります。
三角柱の展開図の特徴としては以下のような事が挙げられます。
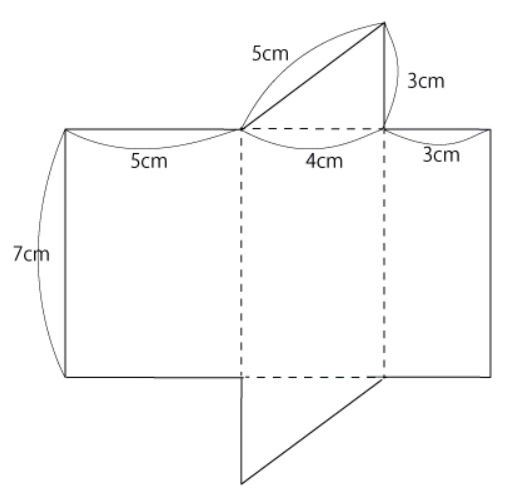
それではこの時の側面積を求めていきましょう。
3つの側面は1つの長方形になることから、大きな長方形として考えていけば大丈夫です。
側面積の縦の長さは、三角柱の高さになるので7cm、横の長さは底面の周りの長さになるので5cm+4cm+3cm=12cmとなります。
よって、側面積は7cm×12cm=84cm²が答えになります。
だんだん難しくなっていきます。
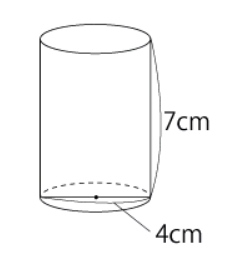
円柱を展開図にすると下図のようになるので見てみてください。
円柱の展開図の特徴としては以下のような事が挙げられます。
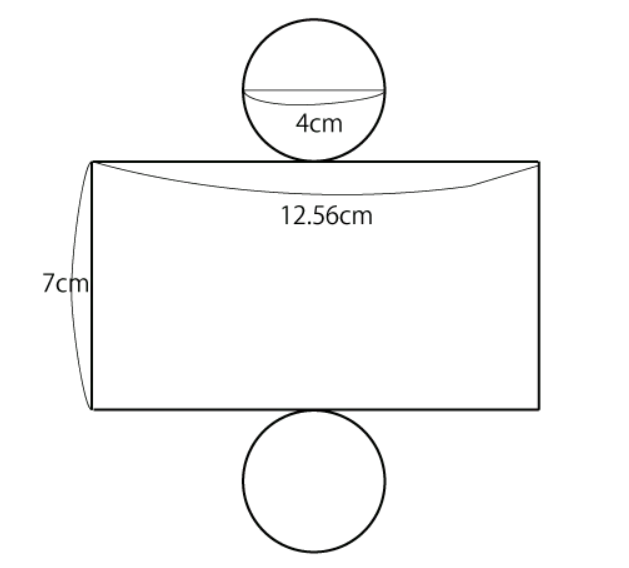
それでは側面積の面積を求めていきましょう。
側面は長方形になるのでこちらも縦の長さ×横の長さで求めれば大丈夫です。
側面積の縦の長さは円柱の高さと同じなので7cm、横の長さは底面の円周に等しくなるので4cm×π=4πcmとなります。(図ではπ=3.14となっています)
よって側面積は7cm×4πcm=28πcm²が答えになります。
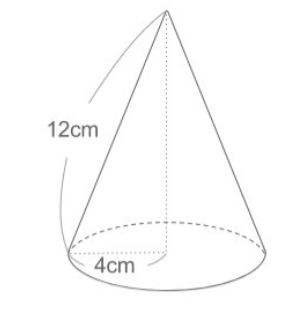
さて、今回の最難関、円錐の展開図を見ていきましょう。図の12cmの場所のことを「母線」と呼ぶので覚えておいてください。
展開図自体は下図のようになります。
円錐の展開図の特徴としては以下が挙げられます。
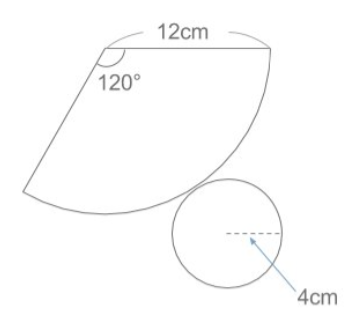
れでは側面積を求めていきましょう。
色んな方法がありますが、まずは正攻法で求めていきたいと思います。
おうぎ形の面積は半径×半径×π×(中心角/360°)で求めることが出来ました。
難しいのはこの時の中心角はどのようになるかですよね。
おうぎ形は円を切り取った形であるということを考えると求めることができます。
半径12cmの円の円周は12cm×2×π=24πcmです。今回のおうぎ形の弧の長さは底面積の円の円周と同じなので4cm×2×π=8πcmだと分かります。
このことからおうぎ形は本来の円の8π/24π=1/3の大きさだと分かります。
よって、中心角は360°×1/3=120°と求めることができ、側面積は12cm×12cm×π×(120°/360°)=48πcm²が答えになります。
この計算、凄く大変だと思います。実は中心角が分からなくても面積を求めることができる裏技が存在します。\
円錐の側面積=母線×底面の半径×π
・・・これで求まります。
早速やってみましょう。
12cm×4cm×π=48πcm²となります。
驚くほど簡単ですね。
これは個人の好みに依りますが、前回の最後に少しだけ触れた公式
おうぎ形の面積=半径×弧の長さ÷2
から導くようにしています。この公式はおうぎ形を三角形のように見立てて、底辺が弧の長さ、高さが半径と考えると覚えやすいです。
展開図の場合、おうぎ形の半径とは母線、弧の長さは底面の円周と等しくなるので
おうぎ形の面積=母線×底面の半径×2×π÷2=母線×底面の半径×π
と導くことができます。







