【数学】立体の体積と表面積

前回は空間図形の色々な立体について学んでいきました。

今回は空間図形の体積や表面積などについて見ていきたいと思います。
ここは苦手にするお子さんが多い分野なのでしっかりと押さえていきましょう！

1.角柱の表面積

角柱とは三角柱や四角柱（立方体や直方体）などを言います。
表面積という新しい言葉が出来てきましたが、「表面の全部の体積のこと」を表面積と呼びます。

表面積＝底面積+側面積で求めることができますが、「表面の全部の体積のこと」と覚えておくと便利です。
早速問題を解きながら学んでいきましょう。

例題1-1

以下の三角柱の表面積を求めよ

解答1-1

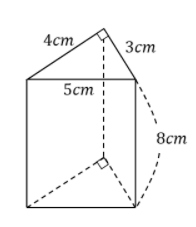
表面積とは「表面の全部の体積のこと」でした。その為展開図を見てみて、全ての面積を足し合わせれば答えになります。

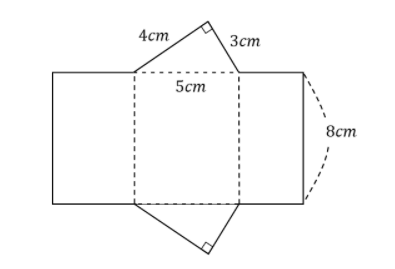
上記を見てみると、三角形の底面積が2枚、長方形の側面積が3枚の計5つの面積の足し算をすればOKです。
底面積：3×4÷2×2＝12ｃｍ²
側面積：5×8+4×8+3×8＝96ｃｍ²

よって、表面積は108ｃｍ²が答えとなります。

例題1-2

以下の直方体の表面積を求めよ

解答1-2

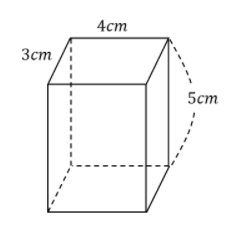
この場合も同じ様に展開図にして考えてみましょう。

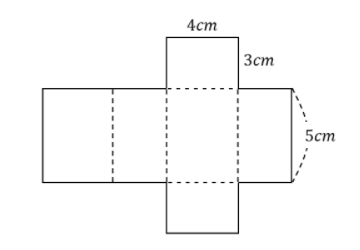
上記を見てみると、底面積が2枚、側面積が4枚の計6つの面積の足し算をすればOKです。
底面積：4×3×2＝24ｃｍ²
側面積：4×5×2+3×5×2＝70ｃｍ²
よって、表面積は94ｃｍ²が答えとなります。

2.円柱の表面積

この章では円柱の表面積の求め方を学んでいきます。
前章で習った通り、表面積とは「表面の全部の体積のこと」と捉えていきましょう。

円柱の表面積は側面積の長方形の横の長さが底面積の円周と同じ大きさになることがポイントです。
早速見ていきましょう。

例題2

以下の円柱の表面積を求めよ

解答2

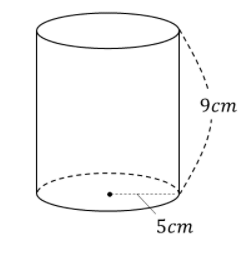
表面積を求めるときには展開図です。やってみましょう！

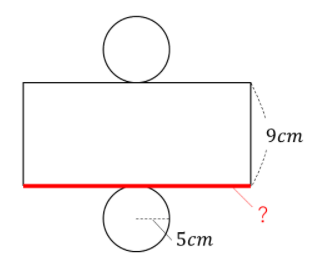
赤線の「？」の部分が重要になってきます。ここは底面積の円周の長さになりましたね。

底面積：5×5×π×2＝50πｃｍ²
側面積：9×（5×2×π）＝90πｃｍ²
よって、表面積は140πｃｍ²が答えになります。

3.角錐の表面積

さて、ここからは「柱」ではなく、「錐」を見ていきたいと思います。
基本の考え方は同じです。表面積は「表面の全部の体積のこと」でしたね。

例題3

以下の四角錐の表面積を求めよ

解答3

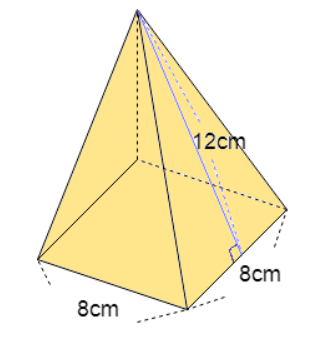
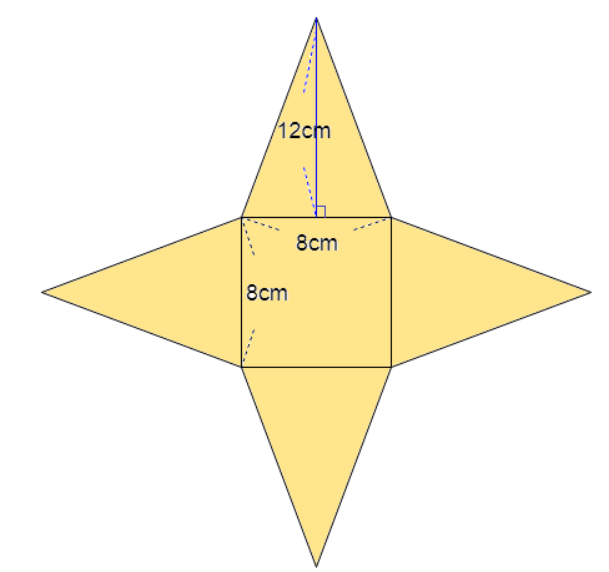
展開図は上記のようになります。底面積が1枚と側面積が4枚の計5つの面積の足し算をすればOKです。
底面積：8×8＝64ｃｍ²
側面積：8×12÷2×4＝192ｃｍ²
よって、表面積は256ｃｍ²が答えとなります。

4.円錐の表面積

次に円錐の表面積を見ていきましょう。くどいようですが、表面積は「表面の全部の体積のこと」です。
円錐の場合のポイントは側面積のおうぎ形の弧の長さが底面積の円周と同じになることです。

例題4

以下の円錐の表面積を求めよ

解答4

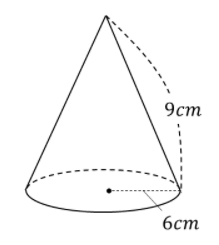
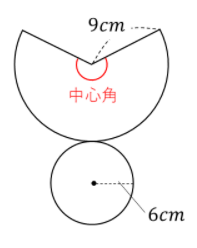
展開図はこのようになります。底面積の円と側面積のおうぎ形の2つに分かれます。
本来であれば中心角の角度を求めておうぎ形の面積を求めていきますが、今回は省略し、半径×弧の長さ÷2で求めていきます。詳しくはこちらの記事で解説しています。

底面積：6×6×π＝36πｃｍ²
側面積：9×（6×2×π【底面積の円周の長さ】）÷2＝54πｃｍ²
よって、表面積は90πｃｍ²となります。