






さて、今回からは一次関数の分野について学んでいきたいと思います!
一次関数は比例の分野と方程式の分野さえ押さえておけば実はとても簡単です!!
ちょっとこの2分野が不安だなぁと言う方はコチラの記事から復習してみてください。
一次関数とは簡単に言うと比例の式に変わらない数(定数項)がついたものということです。
例を見ながら見ていきましょう。
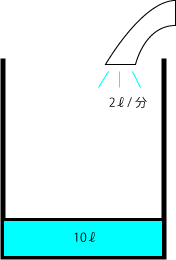
図のように水が10ℓ入った水槽に毎分2ℓの水を入れていくとき、水を入れてからx分後の水の量をyℓとするときを見ていきましょう。
比例の時もそうでしたが、まずは簡単な数をxに当てはめてyがどのように変化するかを考えてみます。
1分後、すなわちx=1の時は水槽の水の量yは2ℓ×1分+10ℓ(もともとあった水の量)=12ℓと求まります。
同様に、2分後は2ℓ×2分+10ℓでy=14ℓ、3分後は2ℓ×3分+10ℓでy=16ℓと求まります。
表にすると
| x(分) | 1 | 2 | 3 | 4 | 5 | ・・・ | 10 |
| y(ℓ) | 12 | 14 | 16 | 18 | 20 | ・・・ | 30 |
のように表せます。
これがもし比例の問題であれば最初に水はなく、単純に1分ごとに2ℓの水が増えていくという問題になっています。
図のようなxとyの関係を式にするとy=2X+10と表現できます。
この式については次項で詳しく解説していきます。
ここでは前項で出てきた式を一般化して、語句を紹介していきたいと思います。
比例の時の一般化した式はy=axで表現しました。
一次関数の場合はy=ax+bという形で表現をします。
ここで、aは比例の時と同じく「変化の割合」や「傾き」と呼びます。
新しく出てくるbの事を「切片」と呼びます。正確には「y切片」と呼びますが、「切片」で覚えておけばOKです。
ここで比例は一次関数の一つでb=0の時の形であるということが確認できたと思います。
次項ではグラフがどうなるのかに注目してみましょう。
それでは実際にグラフに表してみましょう。
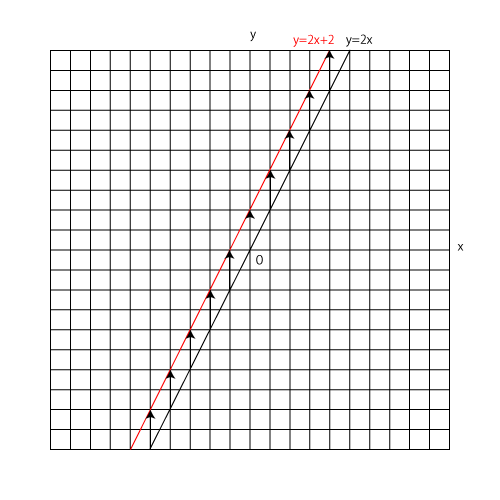
ここでは
黒字:y=2xの比例のグラフ
赤字:y=2x+2の一次関数のグラフ
となっています。
違いは簡単です。
図の矢印に注目してください。
切片の分だけ比例のグラフよりもずれていることが分かります。
今回は切片が2だったので上に2つずれていますが、
切片が3ならば上に3つ、切片が-5ならば下に5つずれることになります。
それでは実際に問題を解きながらグラフの書き方を学んでいきましょう。
次の一次関数のグラフを書きなさい。
(1)y=x+3
(2)y=-3x+1
(3)y=2/3x+2
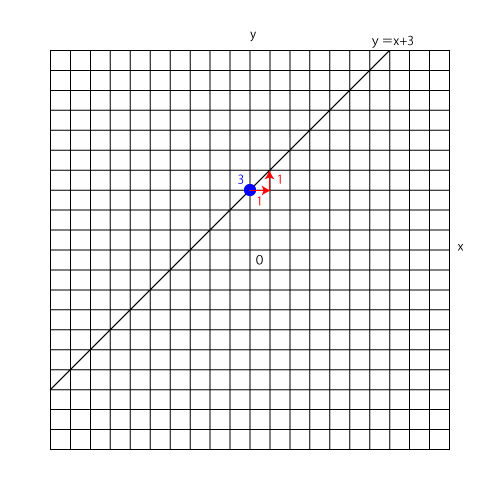
(1)y=xのグラフを書いて上に3つずらすという方法で書いてもいいのですが、発展性が無いので解き方を分かりやすく紹介します。
注目する点は2つだけです。
「切片」と「傾き」です。
y=x+3のグラフは
切片:3
傾き:1
となっています。
ここで「切片=スタート地点」と覚えておいてください。
グラフで言うと青丸の部分です。
次に傾きです。傾きは比例の時にやりましたね。
1=1/1なのでx方向右に1つ、y方向上に1つ移動した点とスタート地点を結びます。
この繰り返しでグラフを書くことができます。
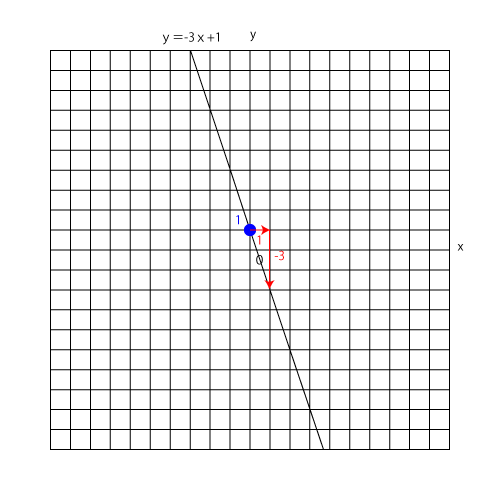
(2)同様にやっていきましょう。
y=-3x+1のグラフの切片と傾きは
切片:1
傾き:-3
となります。
スタート地点が青丸の1、傾きの-3はx方向右に1つ、y方向下に3つ移動した点を結べば完成です。
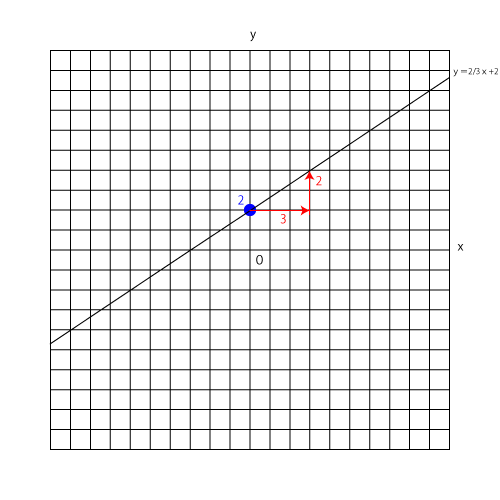
(3)今回も同じ様に解いていきましょう。
y=2/3x+2のグラフの切片と傾きは
切片:2
傾き:2/3
となります。
スタート地点が青丸の2、傾きはx方向右に3つ、y方向上に2つ移動した点を結べば完成です。
このように一次関数のグラフは切片と傾きに注目すれば簡単に書くことができます。
次項では一次関数の式を求めることをやっていきます。方程式の分野の復習が必要になってきます。
\小・中・高校生の勉強にお悩みのある方へ/
ここでは文章から一次関数の式を求めるということを例題と一緒に考えていきたいと思います。
一次関数の基本の式y=ax+bを使うのでしっかり覚えておきましょう。
次の条件を満たす一次関数を求めなさい。
(1)変化の割合が2で、点(2,5)を通る直線
(2)グラフが点(2,1)を通り、切片が5となる
(3)直線y=-x+5に平行で点(2,-4)を通る直線
(4)2点(-3,3)と(3,5)を通る直線
(1)「変化の割合」と「通る点」が分かっているので、基本の式のうち「x,y,a」の3つが分かっていることになります。
これらを基本の式に代入すると、
y=ax+b⇛5=2×2+b
となります。
よって、b=1を解として得るので、一次関数は
y=2x+1が答えとなります。
(2)「切片」と「通る点」が分かっているので、基本の式のうち「x,y,b」の3つが分かっていることになります。
これらを基本の式に代入すると、
y=ax+b⇛1=a×2+5
となります。
よって、a=-2を解として得るので、一次関数は
y=-2x+5が答えとなります。
(3)「平行」というワードがヒントです。平行ということは傾きが等しいということになります。大切な事なので覚えておきましょう。
つまり、「傾き」と「通る点」が分かっているので、基本の式のうち「x,y,b」の3つが分かっていることになります。
これらを基本の式に代入すると、
y=ax+b⇛-4=-1×2+b
となります。
よって、b=-2を解として得るので、一次関数は
y=-x-2が答えとなります。
(4)少し難易度が上がります。連立方程式の理解が必要になってくるので怪しいなという方は復習しておいてください。
今回は「通る点」のみが分かっているので、基本の式のうち「x,y」の2つが分かっていることになります。
このままでは、分からないものが「a,b」の2つあります。今までのように方程式では解けないので連立方程式で解いていきます。
通る点が2点分かっているので、基本の式にそれぞれ代入すると
3=-3a+b,5=3a+b(HPの仕様上「,」で区切っています。)
この時加減法を用いて解くと
a=1/3、b=4を解として得るので、一次関数は
y=1/3x+4が答えとなります。







