






こちらのページでは合同と証明について解説しています!
三角形の合同条件や証明のやり方などを、例題とともに解説しています。授業の予習復習や定期テスト対策にご活用ください!!
形も大きさも同じであることを合同といいます。AとBが合同であることを数学的に表現すると、A≡B となります。
今回はこの合同を数学的に扱っていきます。さっそく例題で雰囲気をつかみましょう!

<例題> かっこの中にあてはまる語をうめましょう。
合同な三角形:△ABC≡△( )
対応する角や辺
辺AC:辺( )、∠ACB:∠( )
<解答>
△JKL、辺JL、∠LJK
今回は三角形の合同にフォーカスをあてて学んでいきます。まずは、三角形が合同であることを示す条件を3つご紹介します。
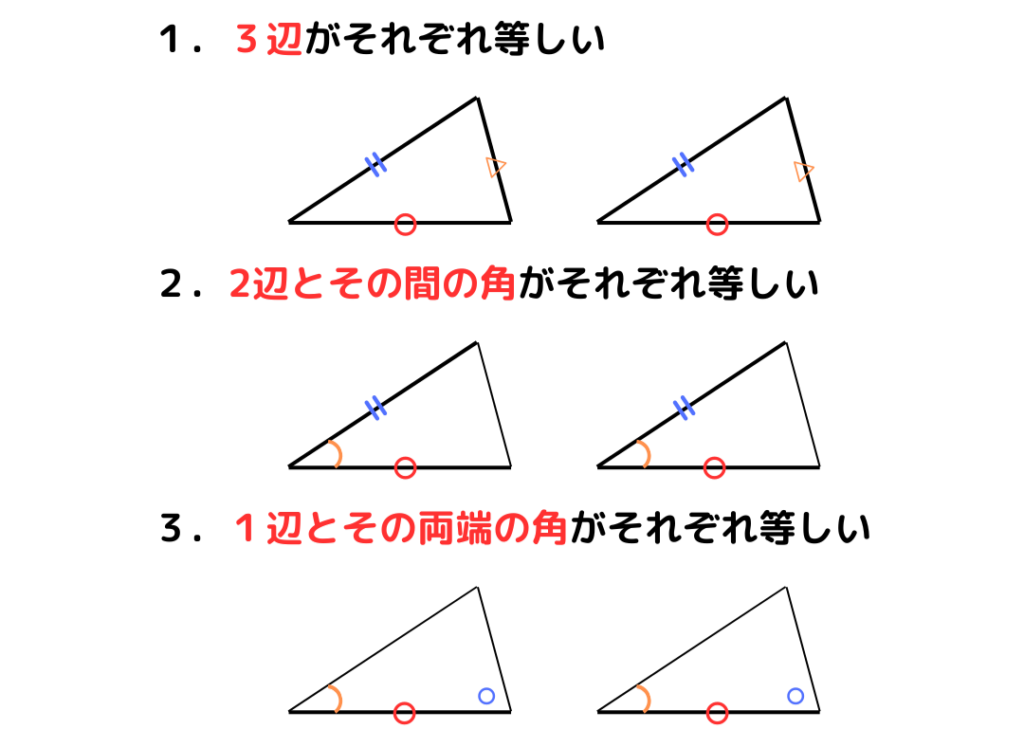
例題を解いて、この3つの条件をどのように使うのかを理解しましょう!
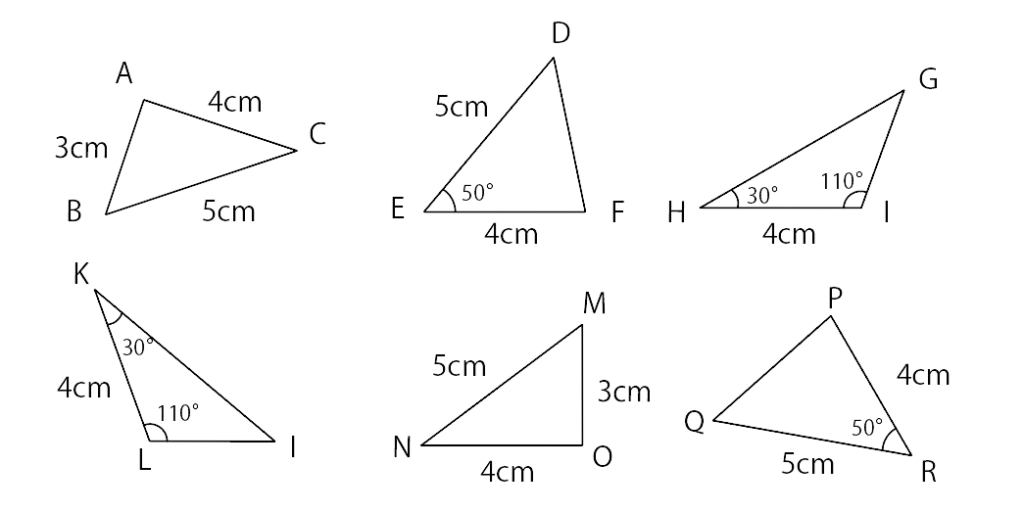
<例題1>
以下の三角形と合同な三角形、正しい合同条件を選びましょう。
△ABC ≡ ( )
合同条件:( )
△DEF ≡ ( )
合同条件: ( )
△GHI ≡ ( )
合同条件: ( )
<解答>
△ABC ≡ △OMN
合同条件:3辺がそれぞれ等しい
△DEF ≡ △QRP
合同条件:2辺とその間の角がそれぞれ等しい
△GHI ≡ △JKL
合同条件:1辺とその両端の角がそれぞれ等しい
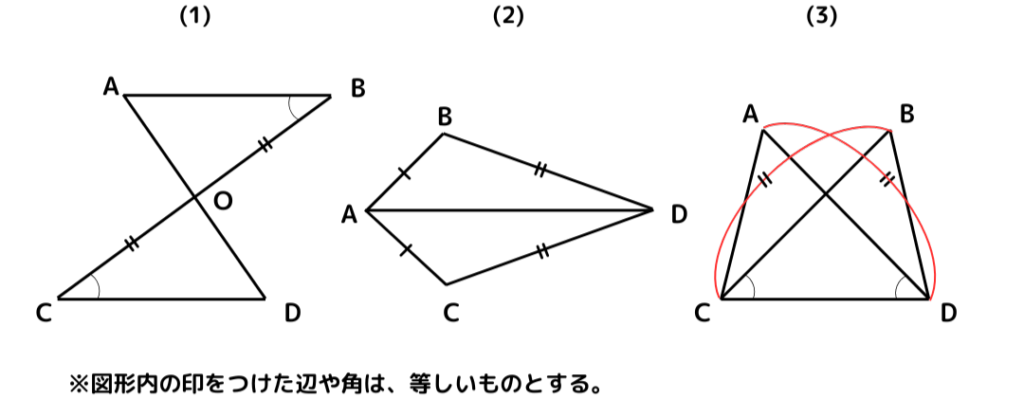
<例題2>
次の図形から合同な三角形を見つけ、その合同条件と共に答えましょう。
(1) △ABO ≡ ( )
合同条件: ( )
(2) △ABD ≡ ( )
合同条件: ( )
(3) △ABD ≡ ( )
合同条件: ( )
\小・中・高校生の勉強にお悩みのある方へ/
<解答>
(1) △ABO ≡ △DCO
合同条件:1辺とその両端の角がそれぞれ等しい
(2) △ABD ≡ △ACD
合同条件:2辺がそれぞれ等しい
(3) △ABD ≡ △BDC
合同条件:2辺とその間の角がそれぞれ等しい
仮定から、(定理を用いて)結論を出すことを証明といいます。どういうことか、ひとつひとつくだいて見ていきましょう。
まず仮定とは、あることを導き出すために、前提として分かっている事がらのことです。例えば【xが3の倍数、yが2の倍数であるとき、xyは6の倍数になる。】とあるとき、「xが3の倍数、yが2の倍数である」が仮定にあたる部分になります。続いて結論は、仮定から新しく導き出されたものを指します。先ほどの例でいう「xyは6の倍数になる」が結論にあたります。
そして、証明をするためには定理が必要になる場合があります。定理とは、前半で紹介した三角形の合同条件にあたるものです。
例題でさらに理解を深めましょう!
<例題>
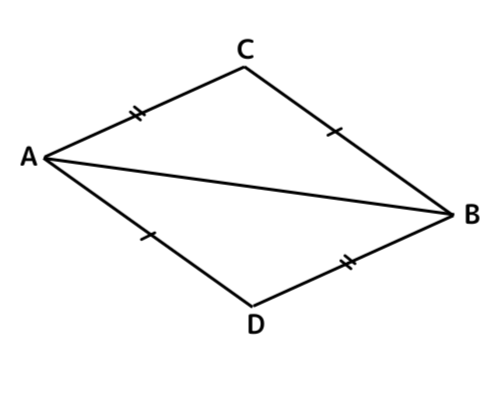
右の図で、AC=BD、AD=BCのとき、AC // BCになる。このことについて、次の問いに答えましょう。
➀仮定と結論を言いましょう。
②仮定から結論を言うには、どの三角形とどの三角形の合同を言えばよいですか。
③仮定から結論が言えることを証明しましょう。
<解答・解説>
➀ 仮定:AC=BD、AD=BC 結論:AD // BC 仮定は前半、結論は後半であることが多いです。
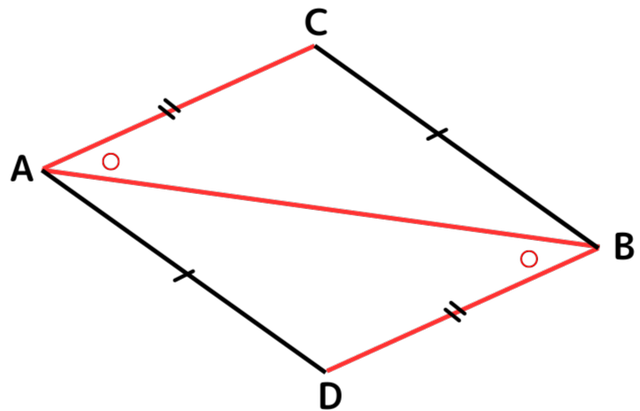
② △ABCと△BAD
平行の特徴は、(同位角や)錯角が等しいということです。つまり、△ABCと△BADが合同であることを証明出来れば、∠CAB=∠DBAが言えて、錯角が等しいことが言えます。三角形の合同を証明することで、平行であることに持っていきます。
③ △ABCと△BADにおいて、AC=BD…➀ BC=AD…②共通する辺なので、AB=BA…③。➀②③より、3辺がそれぞれ等しいので、△ABC≡△BAD 対応する角は等しいので、∠CAB=∠DBA
証明の手順としては、まず初めに合同をいいたい三角形をあげる。次に合同条件を3つあげる。最後に合同条件をあげて、合同をいう。という3つで行います。
以上を踏まえて、練習問題を解いてみましょう!
<練習問題>
下図において、BC=DEであることを証明しましょう。
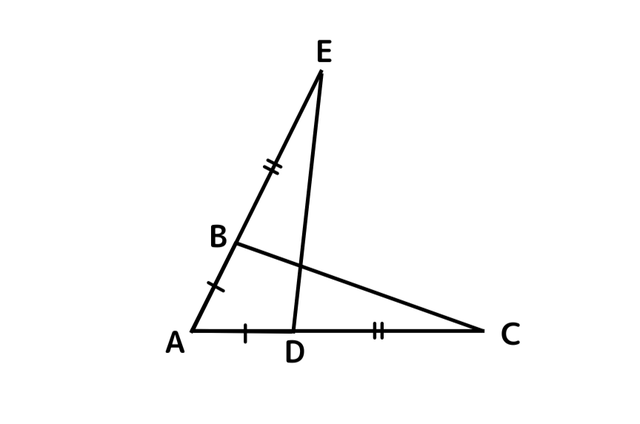
\小・中・高校生の勉強にお悩みのある方へ/
<解答>
△AEDと△ACBにおいて、
AE = AC …①
AD = AB …②
2つの三角形に共通する角なので、∠EAD = ∠CAB…③
①②③より、2辺とその間の角がそれぞれ等しいので、△AED ≡ △ACB
よって、対応する辺は等しいので、BC = DE となる。
最後までお読みいただきありがとうございました。
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください!







