






こちらのページでは二等辺三角形と直角三角形の証明について解説しています。直角三角形の合同条件や証明のやり方などを、例題とともに解説しています。授業の予習復習や定期テスト対策にご活用ください!
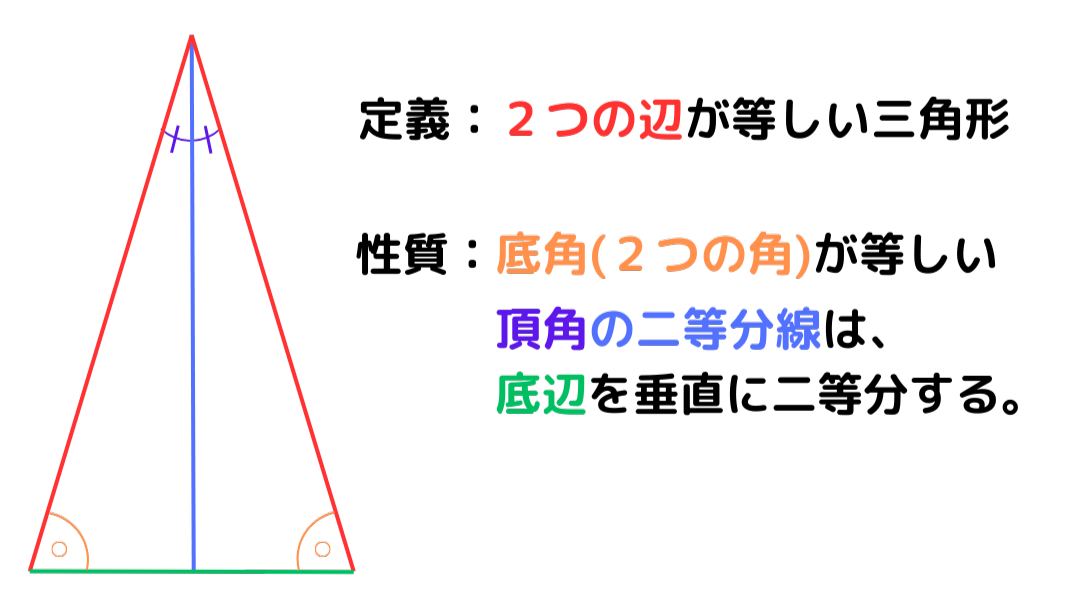
二等辺三角形の証明問題を解くために、まずは二等辺三角形の定義と性質を知っておきましょう。下の図に要点をまとめたので確認しましょう!
以上を踏まえて、まずは底角(2つの角)が等しいことを確認する証明問題を解いてみましょう。
<問題> 二等辺三角形の2つの角が等しくなることを、次のように証明した。下図を参考にして、文中の空らんをうめよう。
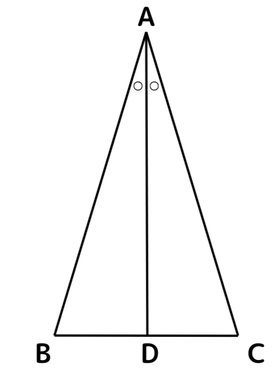
AB=ACである二等辺三角形の頂角Aの二等分線を引き、底辺BCとの交点を Dとした。△BADと △CADにおいて、( ) …①、AB=AC…②共通する辺なので、 ( ) …③
①②③ より、 ( ) がそれぞれ等しいので、△BAD≡△CAD
合同な図形の対応する角は等しいので、 ( )
<解答>
AB=ACである二等辺三角形の頂角Aの二等分線を引き、底辺BCとの交点をDとした。△BADと △CADにおいて、∠BAD=∠CAD …①、AB=AC…②共通する辺なので、AD=AD …③
①②③ より、2つの辺とその間の角がそれぞれ等しいので、△BAD≡△CAD
合同な図形の対応する角は等しいので、∠ABD=∠ACD
今度は、二等辺三角形になるための条件をまとめてみましょう。

先ほどと同じように、条件が正しいことを証明するための問題を解いてみましょう。
<問題>「2つの角が等しい三角形は二等辺三角形である」を、次のように証明した。下図を参考にして、文中の空らんをうめよう。
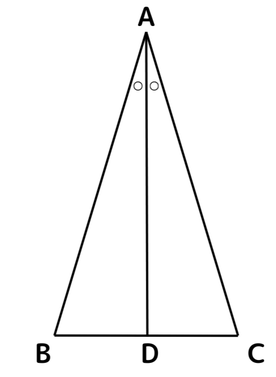
△ABCにおいて、∠Aの二等分線とBCとの交点をDとする。△ABDと△ACDにおいて、 ( ) …①、∠B=∠C…② ①②より、 ( ) …③ 共通する辺なので、AD=AD…④
①③④より、 ( ) ので、△ABD≡△ACD
対応する辺は等しいので、AB=AC
\小・中・高校生の勉強にお悩みのある方へ/
<解答>△ABCにおいて、∠Aの二等分線とBCとの交点をDとする。△ABDと△ACDにおいて、∠BAD = ∠CAD…①、∠B=∠C…②
①②より、∠BDA=∠CDA…③ 共通する辺なので、AD=AD…④
①③④より、1辺とその両端の角が等しいので、△ABD≡△ACD
対応する辺は等しいので、AB=AC
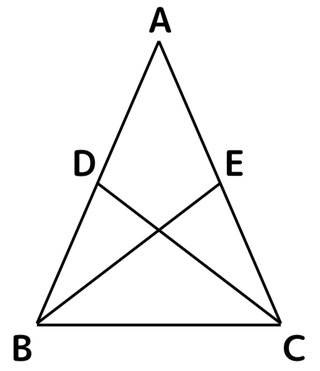
AB=ACである二等辺三角形ABCの辺AB、辺ACの中点をそれぞれD、Eとする。このとき、∠AEB=∠ADCであることを次のように証明した。文中の空らんをうめよう。
△ABEと△ACDにおいて、 ( ) …① D、Eは、それぞれ辺AB、ACの中点なので、( ) …② 共通する角なので、 ( ) …③
( ) がそれぞれ等しいので、△ABE≡△ACD 対応する角は等しいので、∠AEB=∠ADC
<解答>
△ABEと△ACDにおいて、AB=AC…①D、Eは、それぞれ辺AB、ACの中点なので、AE=AD…② 共通する角なので、∠BAE=∠CAD…③
2辺とその間の角がそれぞれ等しいので、△ABE≡△ACD
対応する角は等しいので、∠AEB=∠ADC
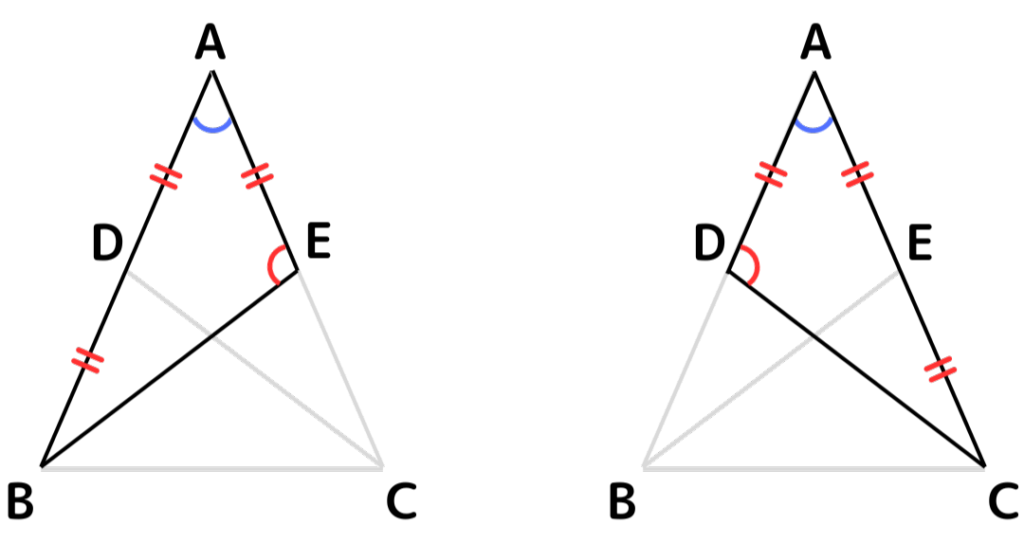
<解説>
∠AEB=∠ADCを言うためには△ABE≡△ACDを証明できればよいです。よって2つの三角形の合同条件を探します。上図のように∠Aは共通&AE=AD。△ABCは二等辺三角形と確定しているので、AB=AC。3つの条件がそろい、「2辺とその間の角がそれぞれ等しい」が言えます。
続いて直角三角形の証明に移ります。直角三角形の証明を行うためには直角三角形の合同条件を知っておく必要があります。下の図にまとめたので確認しましょう!
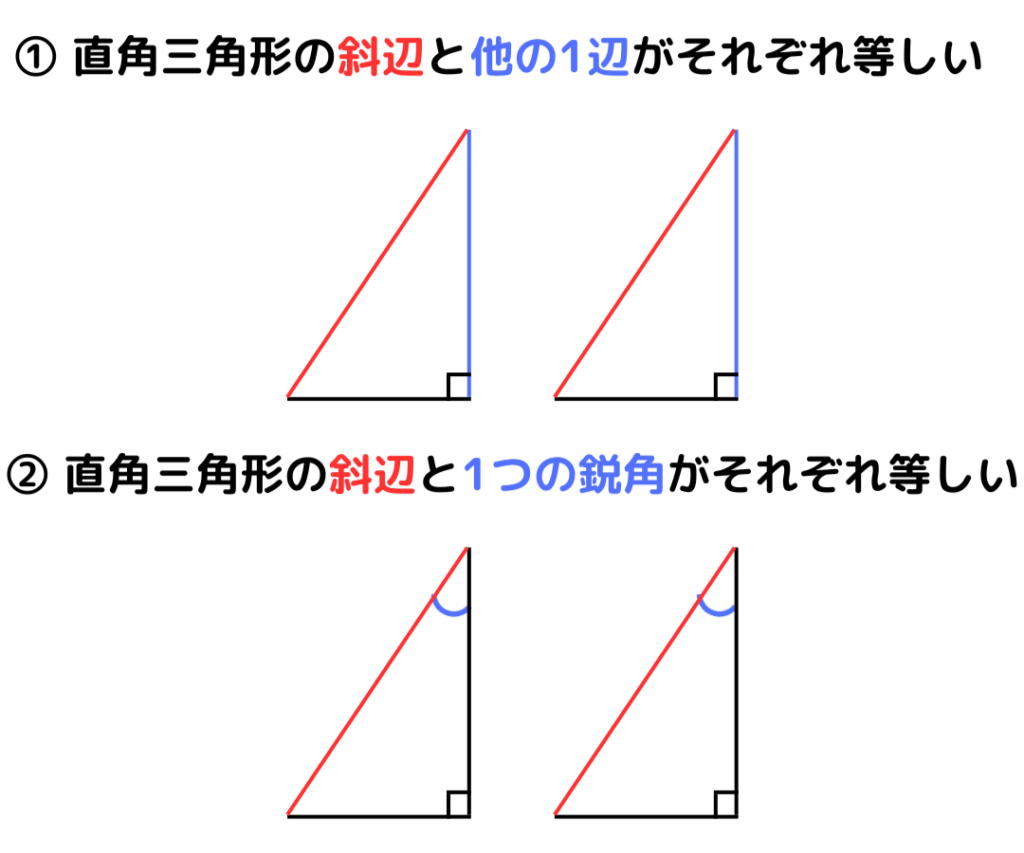
ではこの条件を踏まえて、問題を解いてみましょう。
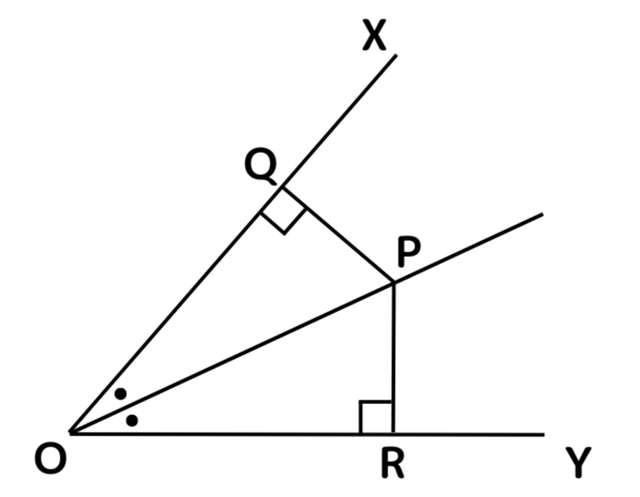
下図のように、∠XOYの二等分線上の点Pから2辺OX, OYに、それぞれ垂線PQ, PRをひく。このとき、PQ=PRであることを次のように証明した。文中の空らんをうめよう。
△OPQと△OPRにおいて、 ( ) =90°…①共通する辺なので、 ( ) …②
OPは∠XOYを2等分するので、 ( ) …③
①②③より、直角三角形の ( ) がそれぞれ等しいので、△OPQ≡△OPR
合同な図形の対応する辺は等しいので、PQ=PR
\小・中・高校生の勉強にお悩みのある方へ/
<解答>
△OPQと△OPRにおいて、∠PQO=∠PRO=90°…① 共通する辺なので、OP=OP…② OPは∠XOYを2等分するので、∠QOP=∠ROP…③
①②③より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、△OPQ≡△OPR
合同な図形の対応する辺は等しいので、PQ=PR
ここまでお読みいただきありがとうございました。最後に「逆」と「反例」についてご紹介します。
例えば、「Aならば、Bである。」とあるとき、Aの部分を仮定、Bの部分を結論といいましたね。この仮定と結論を入れかえることを逆といいます。つまり「Bならば、Aである。」とするわけです。この逆にした文章は、成り立つ場合と成り立たない場合があります。具体例を見てみましょう。
「△ABC≡△DEFならば、AB=DEである。」この文章自体は正しいです。しかし、これを逆にしてみると
「AB=DEならば、△ABC≡△DEFである。」となります。果たしてこれは正しいでしょうか。

上の2つの三角形は確かにAB=DEですが、合同な三角形ではありませんね。つまり、この場合、逆の文章は成立しないことになります。このように、逆にしたときに成り立たない例のことを反例といいます。
最後までお読みいただきありがとうございました。
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください!







