【数学】練習問題あり 四角形の性質と証明
こちらのページではさまざまな四角形の性質や証明について解説しています。平行四辺形の定義や証明のやり方、長方形・正方形・ひし形の性質、等積変形などを例題とともに解説しています。授業の予習復習や定期テスト対策にご活用ください！
目次
1.平行四辺形
まず、平行四辺形について見ていきます。
平行四辺形の定義と性質
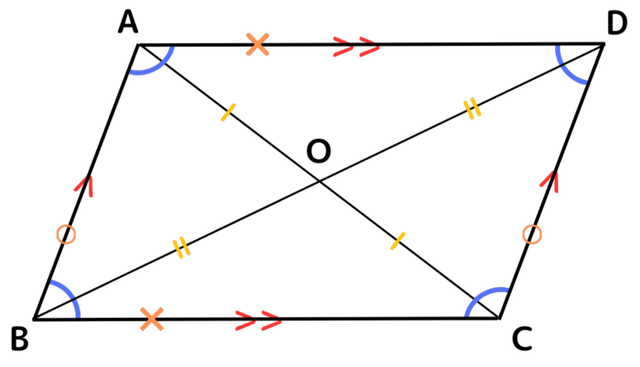
(※ 文字(数学)と図形内の記号の色がそれぞれ対応しています。)
以上が平行四辺形の定義と性質です。
平行四辺形の定義と性質を使った問題として例を挙げると、∠Dが70°であるとき、∠Bは何度か。(③ の性質から∠B＝70°であることが分かります。) や、辺ACが8cmであるとき、辺OAと辺OCはそれぞれ何cmか。(④からOA=OC=4cmであると分かります。) などがあります。
2.平行四辺形の条件と証明
次に、平行四辺形の証明問題と平行四辺形になるための条件を見ていきます。
平行四辺形を使った証明
(問) 平行四辺形ABCDの対角線BD上に、BE=DFとなるような２点E、Fをとると、AE=CFとなる。 このことを次のように証明した。
( A )～( D )に当てはまる記号や言葉を書きなさい。
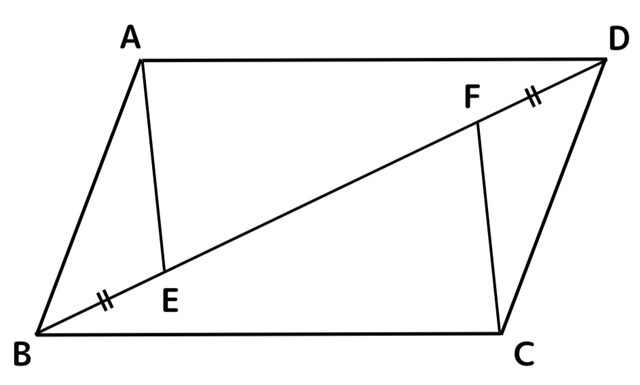
△ABEと△CDFにおいて、仮定より、 ( A ) …①
平行四辺形の対辺は等しいので、 ( B ) …②
( C ) より錯角が等しいので、 ( D ) …③
①②③より、２辺とその間の角が等しいので、△ABE≡△CDF
合同な図形の対応する辺は等しいので、AE=CF
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
模範解答
△ABEと△CDFにおいて、仮定より、 (A : BE=DF)…①
平行四辺形の対辺は等しいので、(B : AB=CD)…②
(C : AB//CD)より錯角が等しいので、(D : ∠ABE=∠CDF)…③
①②③より、２辺とその間の角が等しいので、△ABE≡△CDF
合同な図形の対応する辺は等しいので、AE=CF
解説
①：AE＝CFを証明するためには、△ABEと△CDFの合同を言う必要があります。合同になる条件の１つに、問題文で定義してあるBE＝DFが入ります。問題文に「仮定より、」とあるのでこのBE＝DFのことを指していることが分かります。
②：問題文は「平行四辺形の対辺は等しいので、」と続いています。ということは、平行四辺形の性質その②(記事冒頭)に当てはまります。よって今回の場合は ,AB=DC がいえるということになります。
③：①、②で分かった内容を整理すると、∠ABE＝∠CDFが言えれば、三角形の合同条件である「2辺とその間の角がそれぞれ等しい」が言えることが分かります。∠ABEと∠CDFを見てみると、③の図のようにAB//CDより錯角であることが分かります。よって∠ABE＝∠CDFが言えます。
これで△ABEと△CDFの合同を証明でき、AE=CFも正しいと証明することができました。
平行四辺形になるための条件
平行四辺形には、以下の５つうちどれかを満たしていれば平行四辺形であると言い切ることができます。
１は平行四辺形の定義、2・3・4は平行四辺形の性質と同じことを言っています。
5については、この図のように赤い線(1組の対辺)が同じ長さで平行であれば、その対辺がどこにあっても平行四辺形になるということです。
平行四辺形になることの証明
(問) 平行四辺形ABCDの１組の対辺AD, BCの中点をそれぞれM, Nとすると 四角形MBNDは平行四辺形になることを、次のように証明した。
( A )～( C )に当てはまる記号や言葉を書きなさい。
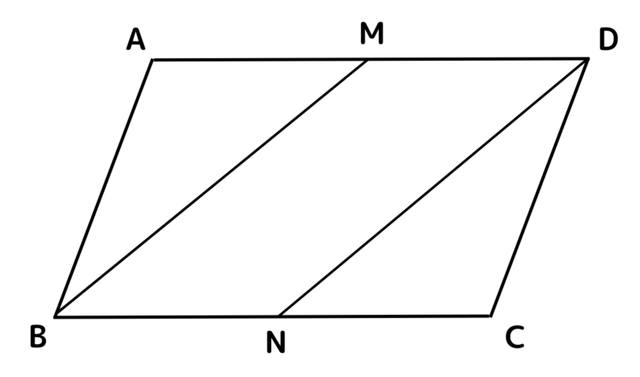
AD//BCより、( A )…①
AD=BCより、( B ) …②
①②より、( C )なので、四角形ＭＢＮＤは平行四辺形になる。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
＜解答・解説＞
模範解答
AD//BCより、(A : MD//BN)…①
AD=BCより、(B : MD=BN)…②
①②より、(C : １組の対辺が等しく平行)なので、四角形MBNDは平行四辺形になる。
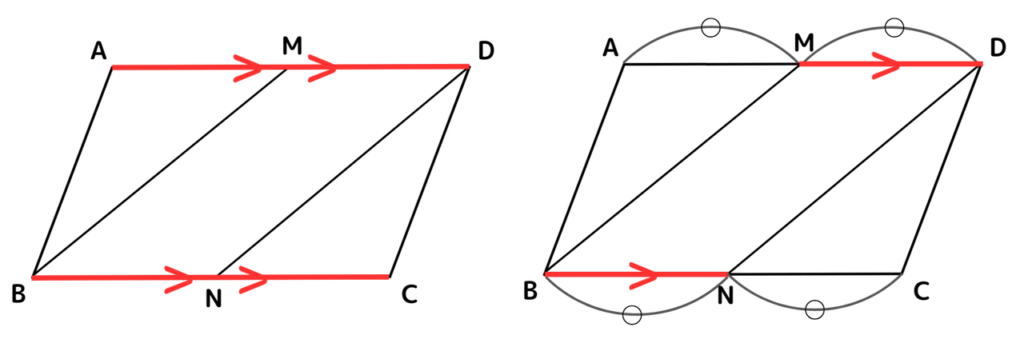
解説
四角形MBNDが平行であることを証明するために、今回は平行四辺形ABCDと辺を共有している辺 MDとBNに着目します。
まず、平行四辺形ABCDはAD//BC、AD=BCなので、その2辺に含まれるMDとBNも平行であると言えます。
次に、問題文にはMとNはそれぞれADとBCの中点であると説明されています。つまり、AM=MD、BN=NCということになります。ADとBCは長さが等しいので、AM=MD=BN=NCとなります。
以上から、MD//BN、MD=BN であることが分かり、平行四辺形になるための条件 ⑤ の「１組の対辺が等しく平行」であることがいえるため、四辺形MBNDが平行四辺形であるということができます。
3.長方形、ひし形、正方形の条件と証明
続いて、長方形、ひし形、正方形の性質と証明を見ていきます。
長方形、ひし形、正方形の定義
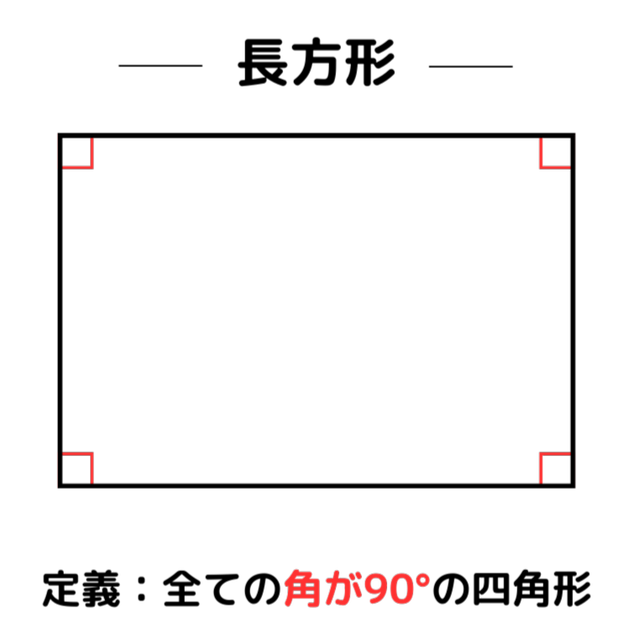
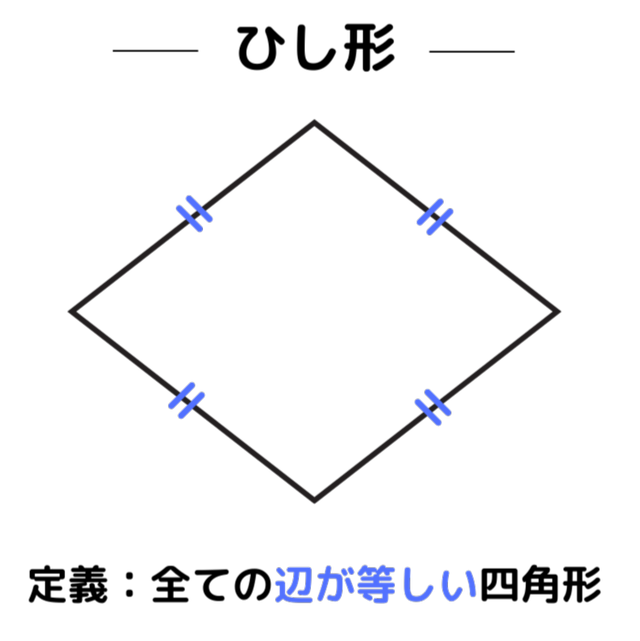
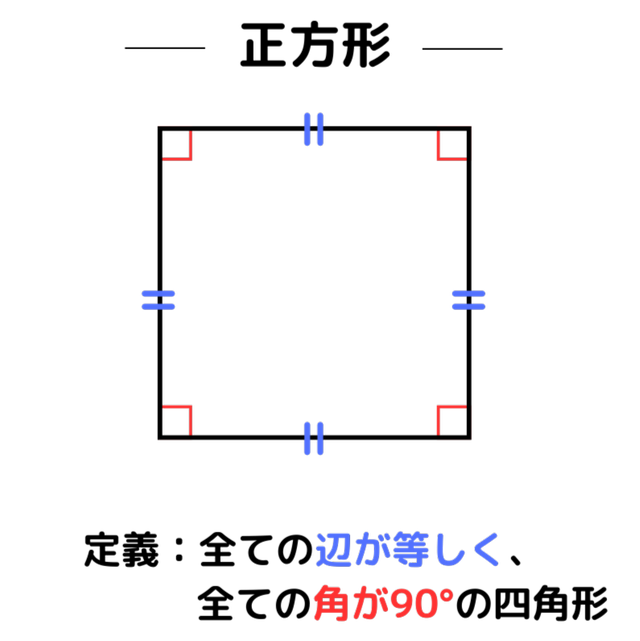
長方形、ひし形、正方形はどれも平行四辺形が元になっています。正方形は、ひし形と長方形の両方の性質を持った四角形です。
また、対角線に注目すると、長方形は対角線の長さが等しく、ひし形は対角線が垂直に交わるという特徴があります。
長方形、ひし形、正方形の問題
(問) 平行四辺形ABCDに次の条件を加えると、長方形、ひし形、正方形のどれになるか。ただし、どれにもならない場合もある。
➀ BC＝CD ② AB=AD、∠BAD90° ③∠ABD＝∠CDB＝90°
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
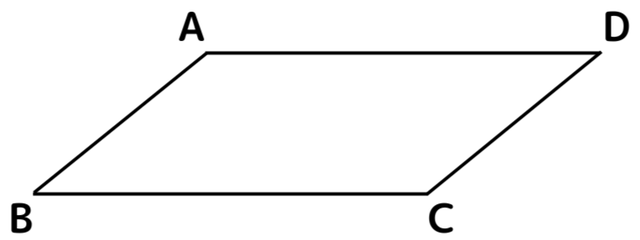
＜解答・解説＞
➀ ひし形 ：平行四辺形は対辺が等しいので、BC・CDの対辺であるAB・ADも長さが等しくなり、全ての辺が等しい平行四辺形となる。
② 正方形：➀ の内容＋１つの角が90°の平行四辺形は正方形になる。
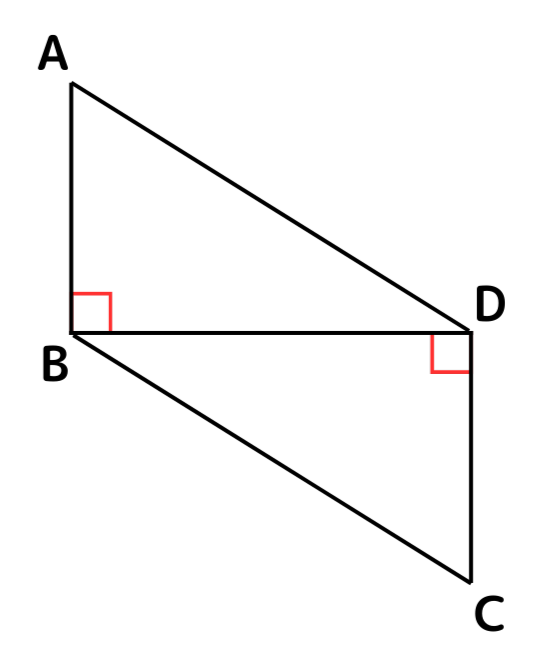
③ 平行四辺形：∠ABDと∠CDBが90°の図形は下のようになる。
4.等積変形
最後に等積変形について解説していきます。
等積変形とは
等積変形とは、面積の大きさを変えないで形を変えることをいいます。
上の図には３つの三角形があります。この３つの三角形はそれぞれ形は違いますが、面積は全て同じになります。これは三角形の面積を求める公式が「底辺×高さ×1/2」であることが理由になります。この三角形は垂直方向の高さが同じで、底辺を共有しているので、「底辺×高さ×1/2」が同じになります。
等積変形の問題
等積変形を使用した問題を解いてみましょう。
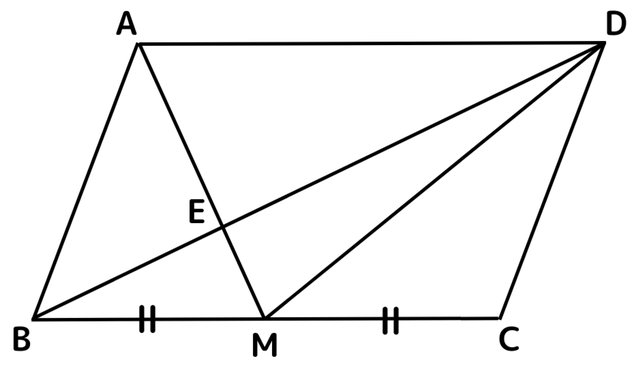
(問) 下の図の平行四辺形ABCDで、Mは辺BCの中点である。このとき△ABMと面積の等しい三角形を全て選びなさい。
＼小・中・高校生の勉強にお悩みのあるお子さん・保護者様へ／
＼小・中・高校生の勉強にお悩みのある方へ／
＜解答＞
△BDM・△CDM
最後までお読みいただきありがとうございました。
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください！
この記事を書いた人
趣味：カメラ
これまで学習アドバイザーとして沢山のお子さんのお悩みを解決してきました。そのノウハウや勉強のコツなどをこの記事を通して発信していきます。
Instagram・ⅹなどでも情報発信中ですので、ぜひフォローください！
