






この投稿では、√が入った計算について解説していきます。a√b と √a の変換や有理化、√の四則計算について練習問題と共に解説していきます。
授業の予習復習や定期テスト対策にご活用ください!
その他の数学の勉強記事もこちらから見ることができます。ぜひご覧ください!
まず例題として、以下の問題を解いてみましょう。
(1) √6×√7
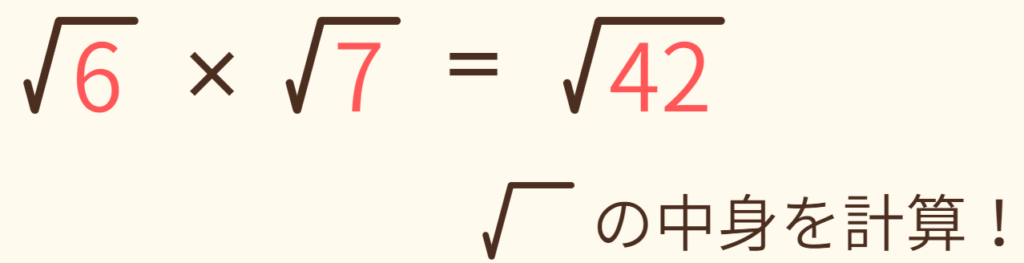
√のかけ算・わり算は √の中身を計算します。
(2) 3√3×2√5

整数がついている√の計算では、√は√同士、整数は整数同士で計算します。
(3) √39÷2√13

割り算を逆数のかけ算に変換して計算します。√39と√13は計算できるので約分もします。
問:次の数を変更して、√a の形にしたとき、根号の中の数(a)はいくつになるでしょう。
(1) 2√6
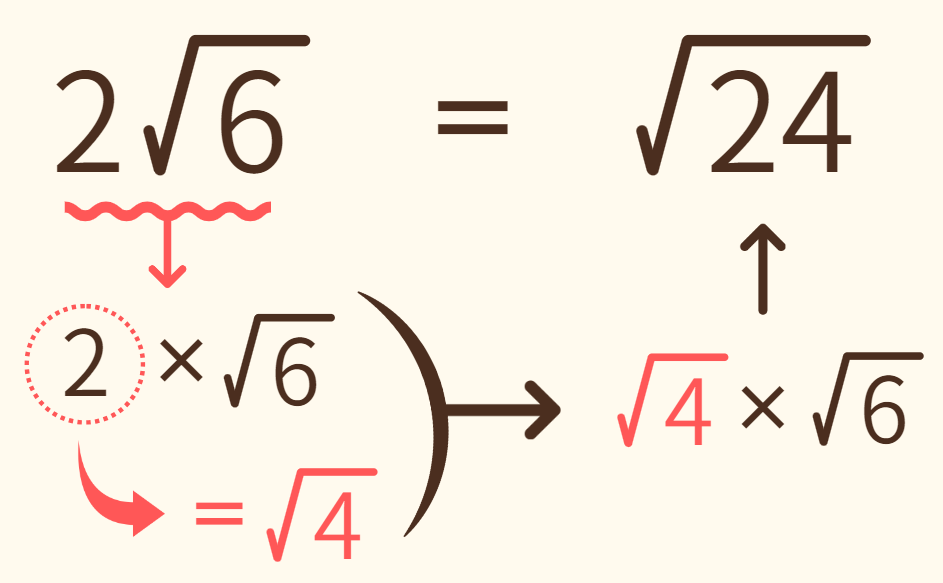
2√6は、2×√6 を省略した形になります。2=√4 なので、2√6は √4×√6=√24 になります。
(2) -5√5
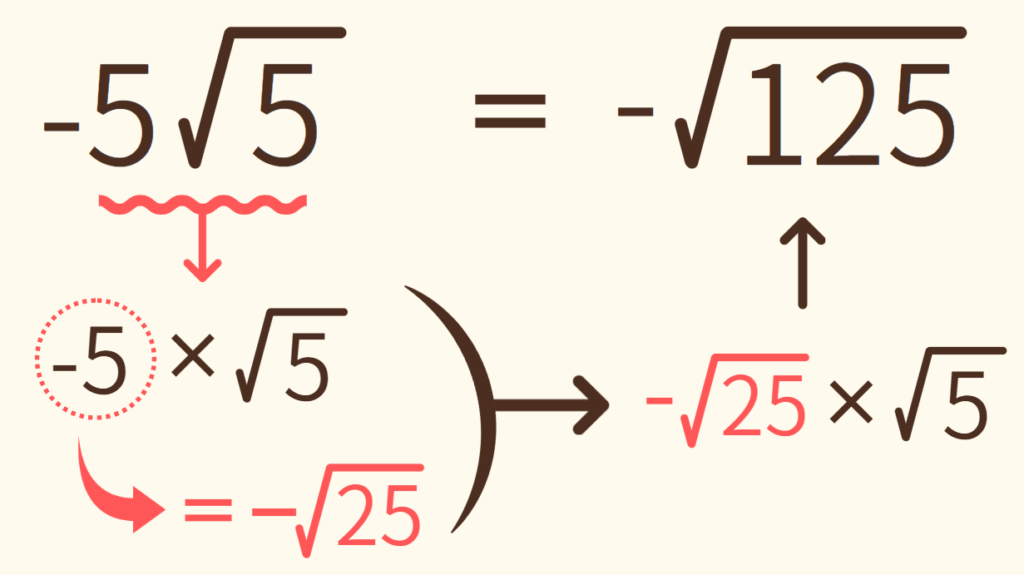
√の外にある整数にマイナスが付いていても解き方は変わりません。
問:次の数の√の中を、できるだけ小さい自然数にしましょう。
(1) √12

√12 は √3 × √4 でできています。√4=2なので、√3 × 2となり、2√3 に変換することができます。
(2)√450

数が大きくなってもやることは変わりません。√のなかの数がどういうかけ算で構成されているかを考えます。
(1) √12 × √28

√12 は √3 × √4、√28 は √7 × √4 でできています。それぞれに √4 があるので、計算すると √ が外れ 4 が生まれます。
(2) 2√6 × 5√3

整数は整数同士、√は√同士で計算します。整数の計算は 2×5=10、 √の計算は √6×√3 = 3√2となります。2つを合わせて 10・3√2=30√2が答えになります。
(3) √5 ÷ √3
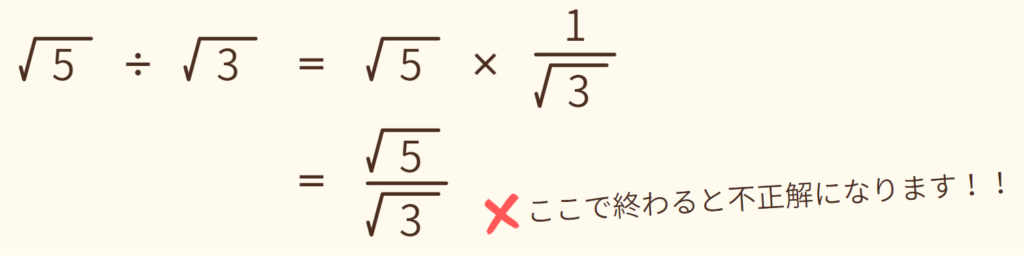
答えが分数の場合、分母が √ だと解答としては不適切です。そこで、有理化ということを行います。
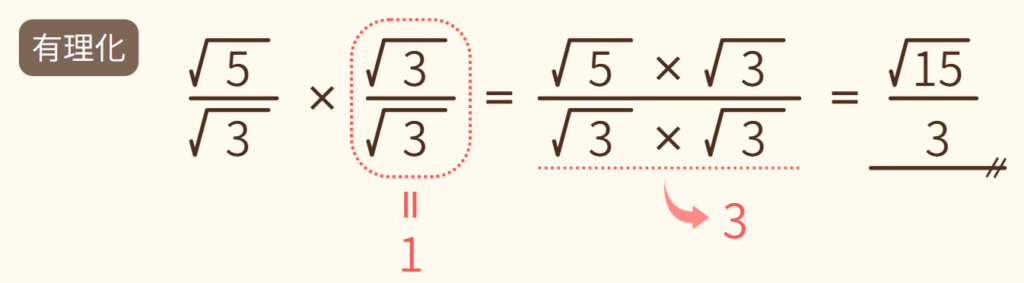
今回の場合、分母が √3 なので、そこに √3 をかけることで分母の √ を取り除きます。しかし、これだけでは元の値を変えることになってしまうので、分子にも同じように √3 をかけます。
ポイント:有理化は分母の √ を外す操作であって、元の値自体を変えるわけではありません。
つまり、結果として既存の値(今回でいう√5/√3) に √3/√3 (=1) をかけるという形になります。元の値に1をかけても、値は変化しないですよね。
(4) -5√2 ÷ √45

まずは √ の中をできるだけ小さい自然数にします。
次に、わり算を逆数のかけ算に変換します。
最後に有理化をして答えになります。
(5) √75 ÷ √24
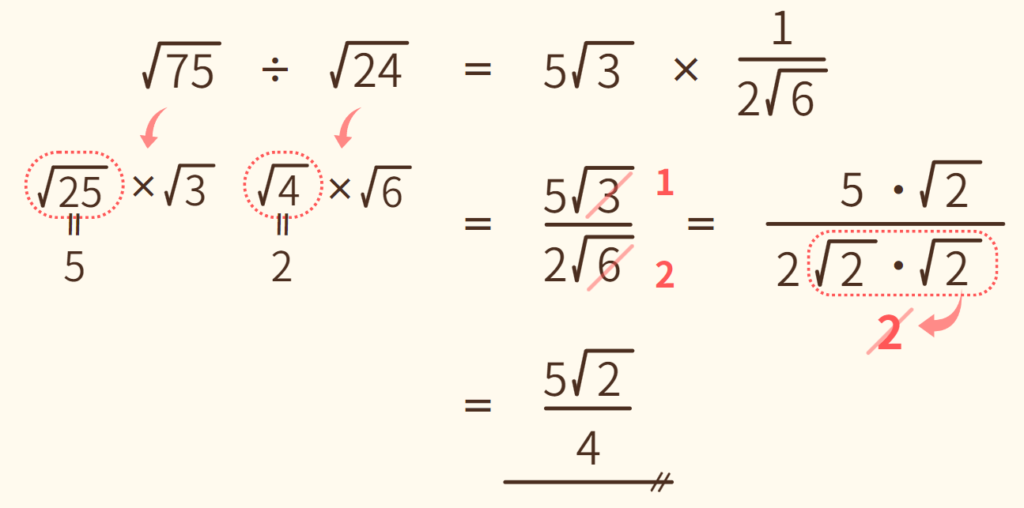
(4)と同じように考えます。√3 と √6 を約分することも忘れないようにしましょう。
\小・中・高校生の勉強にお悩みのある方へ/
(1) 3√2 + 2√2
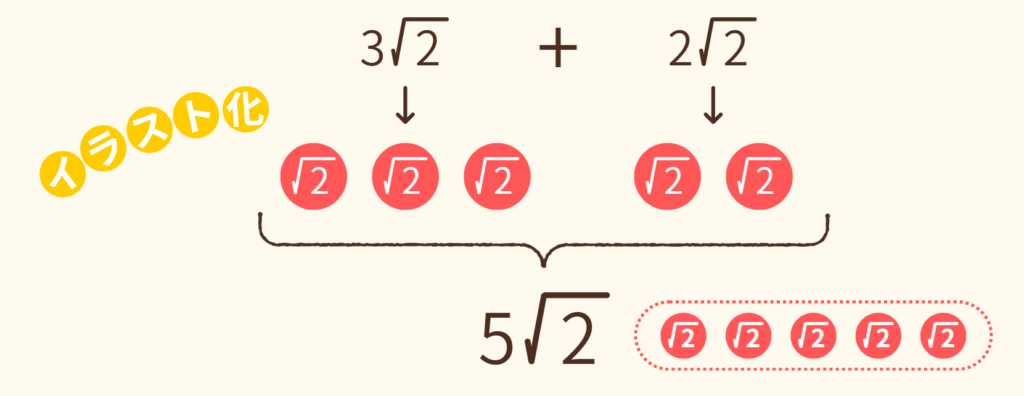
3√2は √2が3個、2√2 は √2 が2個あるということなので、それを足すと√2が5つ、つまり5√2が答えとなります。
このイラストから分かるように、√の中身が同じだと双方を足したり引いたりすることができます。逆に、√のなかの数字が違うと、2つを合わせたりすることはできません。
ポイント:√の加法・減法は、X , Y などの文字の計算と同様に考えましょう。
(2) √12 + √27
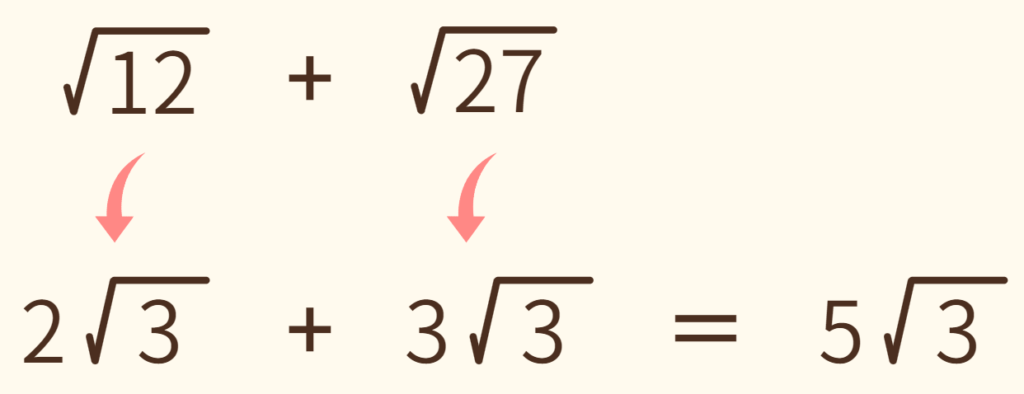
一見 √ の中身が違う数字なので足すことができないように思えますが、√のなかの数字を小さくしてみると計算できるようになります。
(3) √45 + √20 - 2√50 + √18
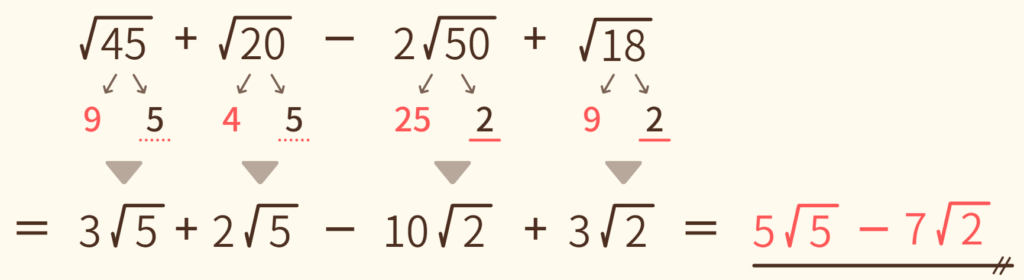
数が増えてもやることは変わりません。√のなかの数字を小さいものにして、√が同じもの同士を計算します。
(4) √72 + 3/√2
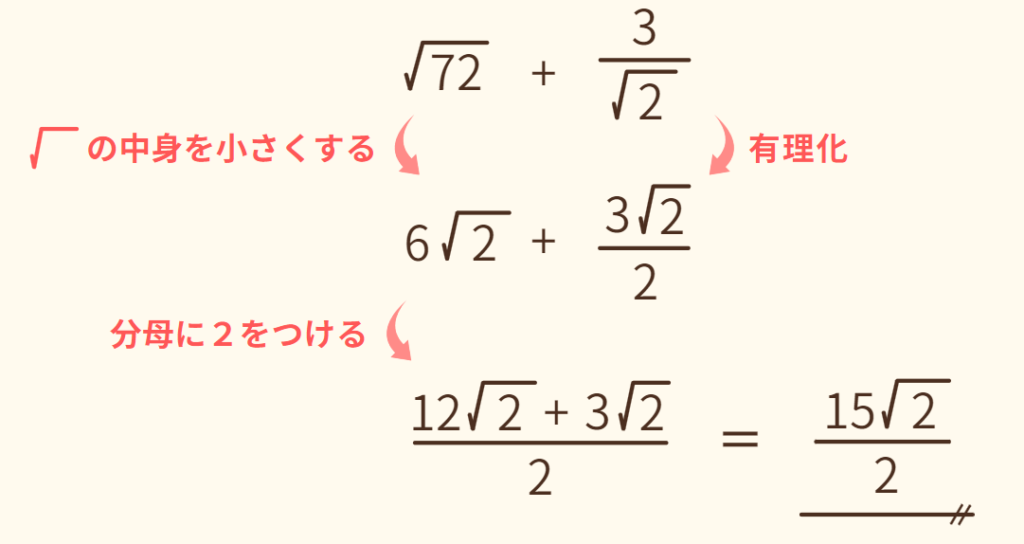
式の中に分数が入っていたら、有理化をして分母を揃えて計算していきます。
(1) √81 - √8 × √32

四則計算は (乗法・除法) → (加法・減法) の順番に計算します。
(2) (√3 + 5)(√3 - 4)
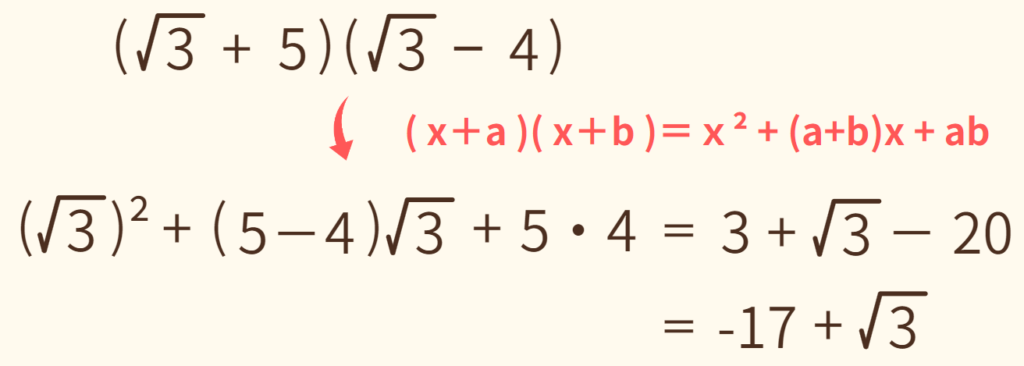
(x+a)(x+b) の乗法公式のxが√に置き換わった計算です。√は2乗すると外れるので注意が必要です。
最後までお読みいただきありがとうございました。
今回は√を含む計算について紹介しました。他にも数学の定期テスト対策の記事があるのでチェックしてみてください!
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。質問などございましたら、お気軽にお問い合わせください!







