






こちらのページでは因数分解について解説しています。因数分解とはなにか、またどうやるのかを練習問題とともに解説していきます。授業の予習復習や定期テスト対策にご活用ください!
その他の数学の勉強記事もこちらから見ることができます。ぜひご覧ください!
まずは、因数分解とはなにかについて解説していきます。
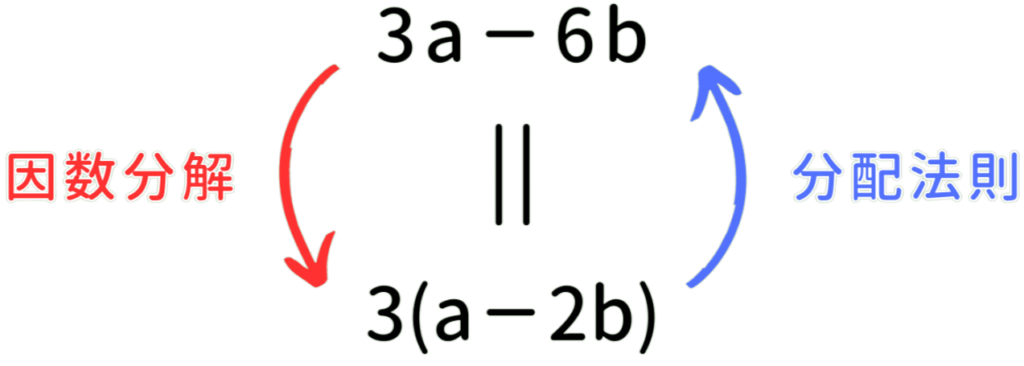
式と乗法公式という範囲を解説した記事で、様々な分配法則についてを詳しく紹介しました。ご覧になっていない方は是非チェックしてみてください!今回解説していく因数分解は、その分配法則の逆、つまり分配された後の式を分配前の状態に戻す計算になります。ここではいろいろな種類の因数分解を見ていきます!
問題)次の式を因数分解しましょう。
x²+5x+6
この問題を解くために必要なるのは下の公式です。
(x+a)(x+b) = x²+(a+b)x+ab
この公式から分かることは、問題にある5と公式にある(a+b)が、6と ab が対応しているということです。
つまり、5は足し算から、6はかけ算から生まれていることになります。
よって、足して5に、かけて6になる数字の組み合わせを見つけることがこの問題の答えにつながります。
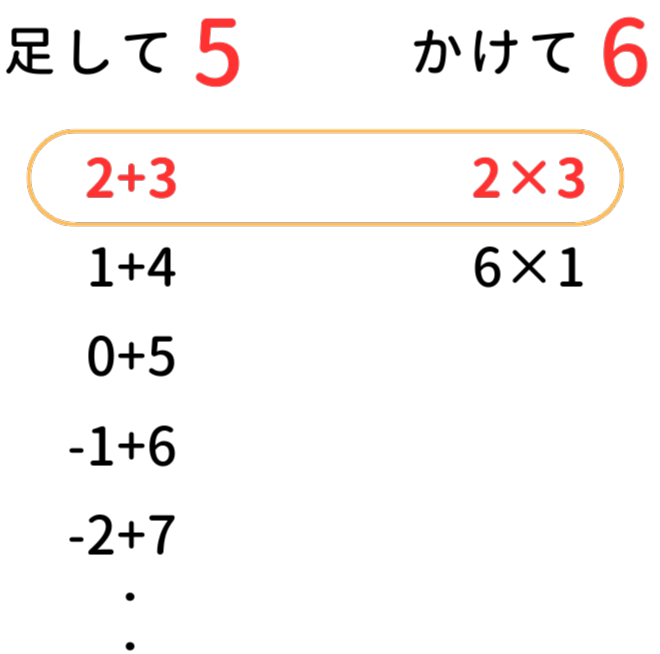
組み合わせを探していくと、2と3が足して5に、かけて6になることが分かります。
(組み合わせを探す際はかけ算から考えると見つけやすいことが多いです。)
これによって、公式のaが2、bが3(もしくはaが3、bが2)ということになり、
(x+2)(x+3) が回答になります。
問題)次の式を因数分解しましょう。
x²+8x+16
この問題も先ほどと同じように、足して8、かけて16になる組み合わせを探していきます。
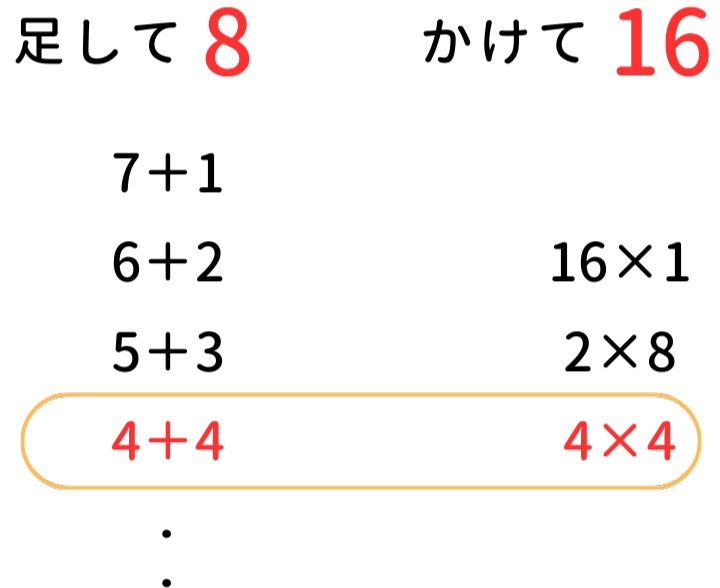
探していくと、4と4が足して8、かけて16になる組み合わせであると分かります。
これを先ほどと同じように公式に当てはめると、
(x+4)(x+4)
となります。( )の中が同じ場合は( )²の形にする必要があるので、式の形を変形します。
よって答えは (x+4)² となります。
分配法則の公式には、( )²の公式もありましたね。
(x+a)² = x²+2ax+a²
\小・中・高校生の勉強にお悩みのある方へ/
問題)次の式を因数分解しましょう。
x²-64
この問題を解くために必要なるのは下の公式です。
(x+a)(x-a) = x²-a²
この公式の a² は問題の 64 にあたります。つまり、aは8になります。よってこの問題の解答は(x+8)(x-8)です。
最後までお読みいただきありがとうございました。
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください!







