







こちらのページでは平方根について解説しています。平方根とはなにか、また平方根にまつわる問題を紹介&解説しています。授業の予習復習や定期テスト対策にご活用ください!
その他の数学の勉強記事もこちらから見ることができます。ぜひご覧ください!
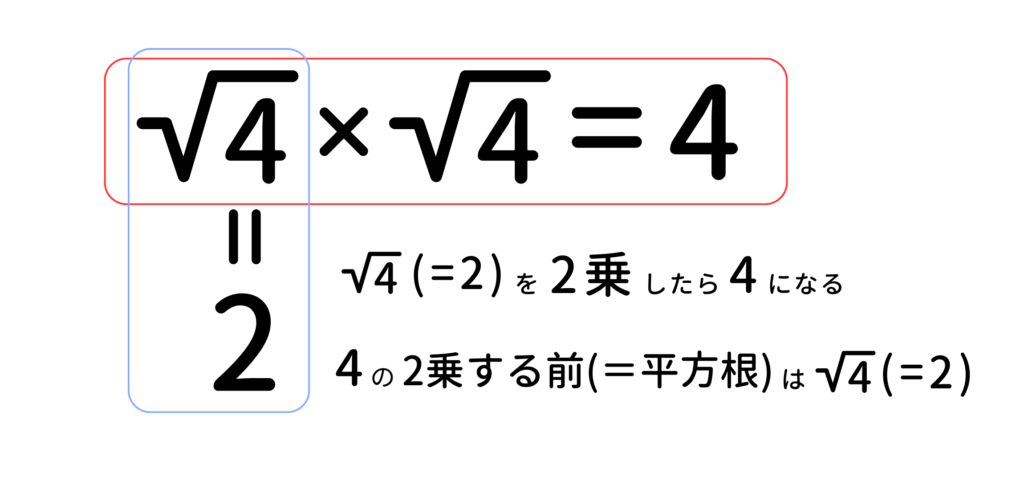
2乗するとaになる数を、aの平方根といいます。平方根が整数や小数、分数で表すことができないときは、√(ルート)の記号を使い、この記号を根号といいます。
例>
4の平方根 → 2,-2(-2×-2も4になるので、4の平方根は2の他に-2も含まれています。2と-2をまとめて±2と表現しても構いません。)
2の平方根は√2、-√2 (±√2) etc.
例題> 次の平方根を答えなさい。
(1) 25/9
答え:±5/3・・・分数の場合も整数と同様、2乗になる前の分子と分母を考えます。
(2) 0.16
答え:±0.4・・・小数点の位置に注意しましょう。
(3) 13
答え:±√13・・・二乗する前の数が整数ではない時に√を使います。
√の大小関係を数直線上に表すと次のようになります。
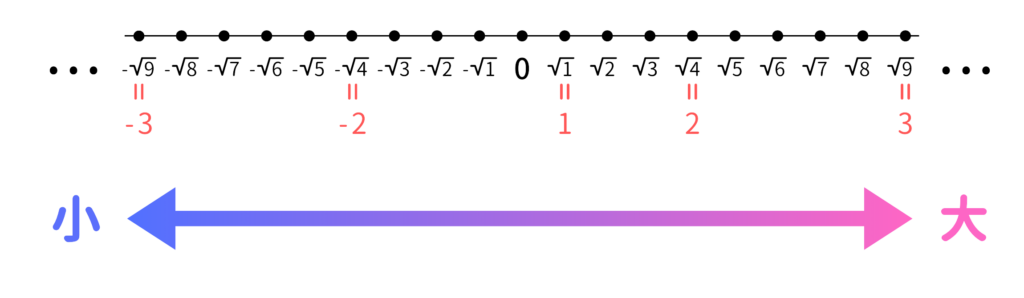
では、上の数直線を踏まえて、-4 と-√15 はどちらが大きいか考えてみましょう。
-4を平方根にする(√をつける)と、-√16 になります。上の数直線からも分かるように、0より小さい世界では数字の小さい方が数は大きいので、-√16 < -√15 となります。よって、-4と-√15 は-√15の方が大きいということになります。
応用問題> 4 <√a<5 にあてはまるような自然数 aの組み合わせを答えましょう。
答え:17, 18, 19, 20, 21, 22, 23, 24
解説:まずこの問題は、4と5を√の状態に変えてから考えます。4と5を√に直すとそれぞれ √16, √25になります。よって元の式は、√16 < √a < √25 となります。次に気を付けなければならないのが不等号の種類です。この問題にある不等号 < ,>は、超過・未満の意味です。(≦,≧は、以上・以下の意味です。)つまり、aには16と25を含めることはできません。よってaは16と25の間にある自然数 17~24になります。
1/2、5/3のように、分数の比で表せる数のことを有理数といい、√2やπ(パイ)のように分数の比で表せない数のことを無理数といいます。
例題>次の数を有理数・無理数に分類しましょう。
(1) 2
答え:有理数・・・2は分数にすると2/1になります。分数にすることができるので有理数です。
(2) 0.75
答え:有理数・・・0.75は分数にすると75/100、さらに約分すると3/4になります。よって有理数です。
(3) √49
答え:有理数・・・√がついているので一見無理数に思えますが、√49=7であるため、有理数になります。
(4) √5/3
答え:無理数・・・分数の中に√5 のような無理数があれば、分数全体も無理数となります。
\小・中・高校生の勉強にお悩みのある方へ/

例えば、π(パイ) ≒ 3.141592…や、√2≒1.41421356…のように、完全な値ではないが、それに近い値のことを近似値といいます。また、近似値と真の値と差を誤差といいます。
例題> 小数点第二位を四捨五入して示す温度計が、26.0℃ を示しています。このときの実際の気温 tの範囲を、不等号を使って表した時、( )に当てはまる数字を答えましょう。
( )≦ t <( )
答え:(25.95)≦ t <(26.05)
では、例題にあった 26.0 と 26 の違いは何でしょうか。これは、数値としては同じですが、有効数字が違います。有効数字とは、意味のある数字や確実に信頼できる数字という意味で、ここでいう26.0 は有効数字3ケタ、26 は有効数字2ケタと表現します。
どういうことか、もう少し詳しく解説していきます。

また、有効数字は「整数部分が1ケタの小数×10の累乗」の形で表すことが多いです。整数部分が1ケタの小数とは、小数点より上の数字が1ケタしかない小数という意味で、10の累乗とは 10²,10³,10⁴…といった値のことです。
では、これまでの内容を元に、例題を解いて理解を深めましょう。
例題> Aさんの家から学校までの距離 839mを、有効数字が2ケタの「整数部分が1けたの小数×10 の累乗」のかたちで表しましょう。
答え:8.4×10²
解説:考えなければならないことは、839という3ケタの有効数字を2ケタに変換すること、変換した数を整数部分が1ケタの小数に変えることです。まず、839の3ケタ目にあたる一の位を四捨五入して840 とします。次に、840の中から整数部分が1けたの小数を作り出します。つまり、840を8.4×100と書き換えるのです。これで839の中から有効数字が2ケタかつ整数部分が1ケタの小数が作れました。最後に100を10の累乗のかたちで表し、答えは8.4×10²です。
最後までお読みいただきありがとうございました。
他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください!



