この投稿では、二次方程式について解説していきます。二次方程式を因数分解・平方根・解の公式・平方完成を使って解く方法について練習問題と共に解説していきます。

授業の予習復習や定期テスト対策にご活用ください！

その他の数学の勉強記事もこちらから見ることができます。ぜひご覧ください！

1. 二次方程式ってなに？

まずは二次方程式とはどういうものなのかを確認しましょう。

二次方程式とは、二次式でできた方程式のことです。　そのままですね(笑)

でも、二次式ってなんだっけ…と思った方もいるかもしれません。

二次式とは、2乗が入った式のことです。

これで二次方程式がどういうものなのか分かりましたね。

では、ここからは二次方程式を色々な方法で解いていきます。

2. 因数分解を使って解く

まずは因数分解を使って解いていきます。

例題１）x² + 5x + 4 = 0 を因数分解を使って解きなさい。

解き方

x² + 5x + 4 を因数分解します。(x+1)(x+4)となりますね。（因数分解の詳しいやり方はこちらから！）

(x+1)(x+4) = 0 と方程式を変えることができればｘの値を求めることができます。

(x+1)(x+4)は、(x+1)×(x+4)ということなので、どちらかの( )の中が０であればかけ算の答えも０となるため、(x+1)(x+4) = 0 が成立しますよね。

つまり、ｘ＝－１，－４が答えになります。

3. 平方根を使って解く

次に平方根を使って解いていきます。

例題２）(1) x² = 16 を解きなさい。

(2) x² = 3 を解きなさい。

(3) 9x² = 10 を解きなさい。

解き方

まず、平方根についてよく分からないなと思った方はこちらのページで詳しく解説しているのでご覧くださいね。

(1) は簡単ですね。16の平方根は４と－4なので、答えはｘ＝±4　となります。

(2) については平方根が整数ではないので√を使用します。答えはｘ＝±√3 です。

(3) は左辺の９が邪魔なので両辺を９で割ってｘ²＝10/9とします。そうしたら後は(2)と同様です。ただし、最後に有理化を忘れないようにしましょう。答えはｘ＝±√10/3 となります。

4. 解の公式を使って解く

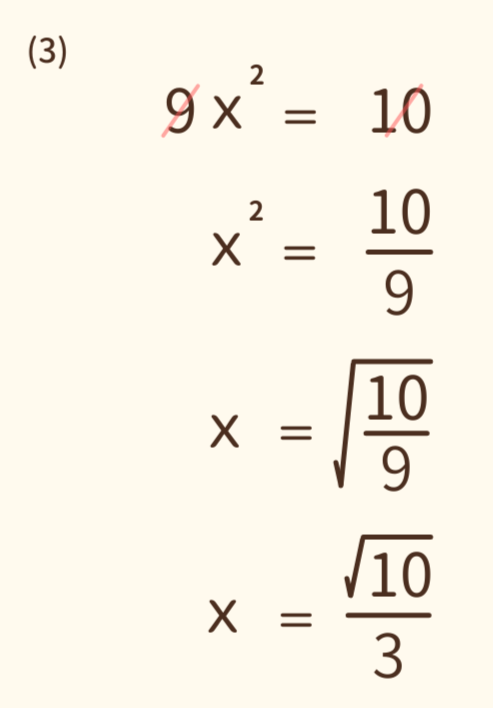
続いて解の公式を使って解いていきます。

例題３） 2x² + 3x -3 = 0 を解きなさい。

解き方

下の式が解の公式になります。この a , b , c にそれぞれ該当する数字を当てはめてみましょう。

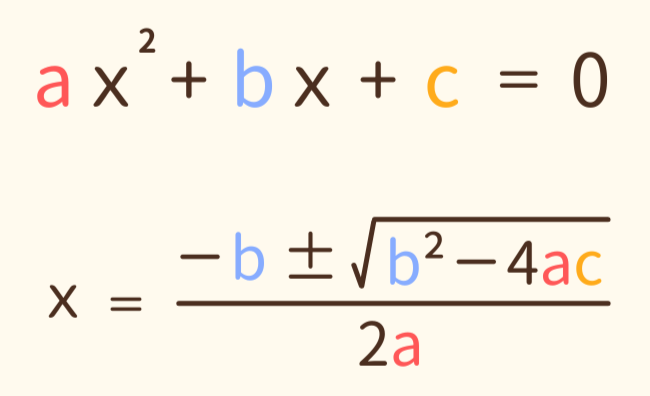
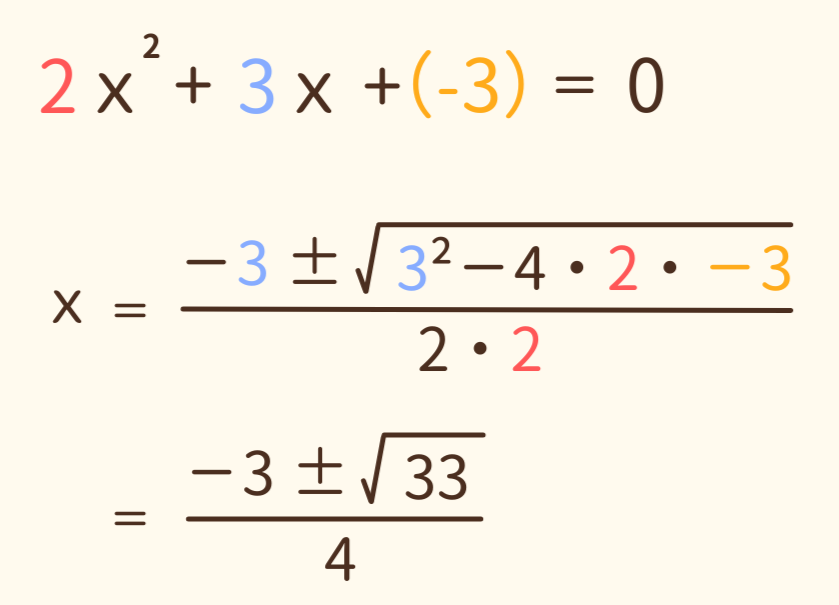
このようにー３±√33/4 が答えになると分かります。

解の公式を使った解き方は万能である代わりに計算が複雑になるのが特徴です。そのため、因数分解や平方根などで解けない時に使うのがオススメです。

＼小・中・高校生の勉強にお悩みのある方へ／

5. 平方完成を使って解く

最後に、平方完成を使って解いていきます。平方完成とは (ｘ+ 〇)² の状態を作ることを指します。

例題４）x² + 6x +2 = 0 を解きなさい。

解き方

まず (ｘ+ 〇)² の状態を作ります。今回の場合は x² + 6x +2 なので、(ｘ+３)² にすると x² + 6x + 9となるので適切です。

ただ、このままだとx² + 6x + 9 なので元の式の x² + 6x +2 と比べると７多いですね。なので －７します。

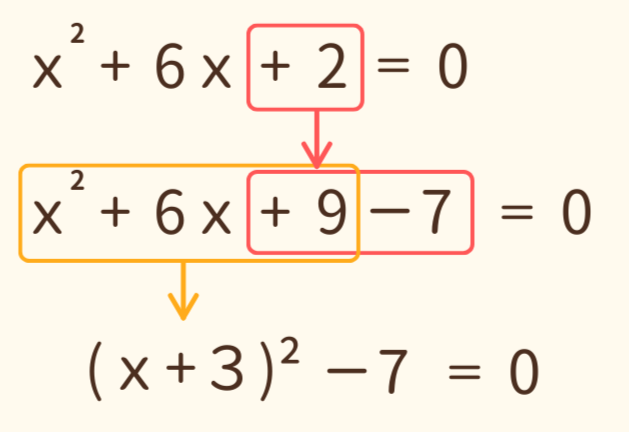
(ｘ+３)²－7 ＝ 0 と式を変更することができたら、ｘ＝〇 の形に式を変えていきます。

まず、ー７を移項します。→ (ｘ+３)² ＝ 7

次にｘ²の2乗をとります。 → ｘ+３ ＝±√ 7

最後に+３を移項して、ｘ＝－３±√7 となり、これが答えとなります。

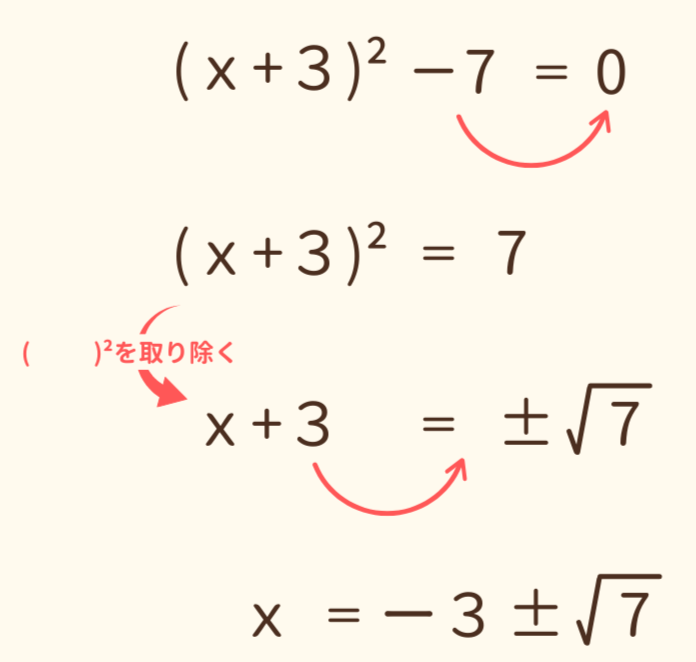
最後までお読みいただきありがとうございました。

他にも様々なお役立ち情報をご紹介しているので、ぜひご参考にしてください。
質問などございましたら、お気軽にお問い合わせください！